 |
Вопрос 2. Задание булевых функций формулами алгебры высказываний. Разложение булевых функций по переменным
|
|
|
|
ПРЕДСТАВЛЕНИЕ ЛОГИЧЕСКИХ ФУНКЦИЙ ФОРМУЛАМИ АЛГЕБРЫ
ВЫСКАЗЫВАНИЙ. СПЕЦИАЛЬНЫЕ РАЗЛОЖЕНИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
- Суперпозиция булевых функций.
- Задание булевых функций формулами алгебры высказываний. Разложение булевых функций по переменным.
- Нормальные формы булевых функций.
- Принцип двойственности для булевых функций. Самодвойственные функции.
Вопрос 1. Суперпозиция булевых функций
Основной операцией, которую можно производить над булевыми функциями, является операция образования сложной функции или суперпозиция булевых функций.
О.1.1. Суперпозицией булевых функций f1, f2, …, fm называется функция f, полученная с помощью подстановок этих функций друг в друга на места переменных, а так же с помощью переименования переменных.
Пример 1.
1. Если f1(u,x3) = u Ú x3, f2(x1,x2) = x1 Ú x2, то суперпозицией этих булевых функций является функция f(x1,x2, x3) = f1(f2(x1,x2),x3) = (x1 Ú x2) Ú x3.
2. Если f1(u,v) = u·v, f2(x1,x2) = x1 Ú x2, f3(x1,x3) = x1 Ú x3, то суперпозицией этих булевых функций является функция f(x1,x2, x3) = f1(f2(x1,x2), f3(x1,x3)) = (x1 Ú x2)·(x1 Ú x3).
Существуют такие булевы функции, через которые выражаются все (вообще все, от любого числа переменных) булевы функции. Этим замечательным свойством обладают вместе взятые конъюнкция, дизъюнкция и отрицание.
Т.1.1. (о представлении булевых функций через конъюнкцию, дизъюнкцию и отрицание)
Всякая булева функция f(х1,х2,…,хn) может быть представлена в виде суперпозиции конъюнкции, дизъюнкции и отрицания, причем знак отрицания относится только непосредственно к переменной и не относится ни к одной из внутренних скобок.
Вопрос 2. Задание булевых функций формулами алгебры высказываний. Разложение булевых функций по переменным
|
|
|
Установим соответствие между булевыми функциями и формулами алгебры высказываний.
Определим взаимно-однозначное соответствие между элементарными переменными высказываниями и булевыми переменными, а так же между знаками логических связок и одноименными булевыми функциями. Скобкам поставим в соответствие те же скобки. Тогда каждой формуле алгебры высказываний соответствует единственная булева функция, а каждой булевой функции соответствует формула алгебры высказываний.
В силу т.1.1 всякая булева функция f(х1,х2,…,хn) может быть представлена некоторой формулой алгебры высказываний с помощью набора логических операций {Ù,Ú,¯}.
Т.2.1. (дизъюнктивное разложение булевой функции по совокупности переменных)
Каждую функцию алгебры логики f(х1,х2,…,хn) при любом m (1 ≤ m ≤ n) можно представить следующей формулой алгебры высказываний:
 (1)
(1)
где дизъюнкция берется по всевозможным наборам значений переменных х1,х2,…,хm;  - условное обозначение переменной хk или ее отрицания, т.е.
- условное обозначение переменной хk или ее отрицания, т.е. 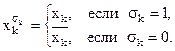
Формула (1) – формула дизъюнктивного разложения булевой функции f(х1,х2,…,хn) по m переменным х1,х2,…,хm. Данная формула справедлива и для разложения не только по первым m переменным.
Следствие 1. (дизъюнктивное разложение булевой функции по одной переменной)
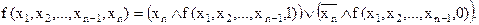
В этом случае функции f(х1,х2,…,хn-1,1) и f(х1,х2,…,хn-1,0) называются компонентами разложения.
Следствие 2. (дизъюнктивное разложение булевой функции по всем переменным)
 (2)
(2)
Если f(х1,х2,…,хn) ¹ 0, то
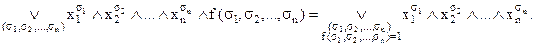
Аналогично можно записать конъюнктивные разложения булевой функции.
1. Конъюнктивное разложение булевой функции по совокупности переменных:

2. Конъюнктивное разложение булевой функции по одной переменной:
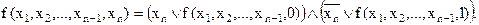
3. Конъюнктивное разложение булевой функции по всем переменным:
 (3)
(3)
Если f(х1,х2,…,хn) ¹ 0, то
|
|
|

Замечание
1. Представление булевых функций с помощью формул алгебры высказываний неоднозначно, так как одна и та же булева функция может иметь несколько различных формульных выражений.
2. Если формулы А и В равносильны, то соответствующие им булевы функции fА и fВ равны.
3. Постоянные булевы функции – константа 1 и константа 0 – могут быть представлены соответственно тождественно истинными и тождественно ложными формулами алгебры высказываний.
|
|
|


