 |
Вопрос 3. Нормальные формы булевых функций
|
|
|
|
Из сказанного выше следует, что всякая булева функция может быть представлена некоторой формулой алгебры высказываний, причем такое представление неоднозначно. В частности, одной из таких представляющих формул будет СДНФ (если данная булева функция не является константой 0) или СКНФ (если данная булева функция не является константой 1).
Отыскав совершенную нормальную форму для формулы алгебры высказываний, представляющей данную булеву функцию, можно перейти от этой формы к формульному выражению для данной булевой функции. Его называют совершенной (дизъюнктивной или конъюнктивной) нормальной формой данной булевой функции (СДНФ и СКНФ соответственно). Каждая из них для данной булевой функции, если она существует, единственна.
Т.3.1. (о функциональной полноте)
Для любой булевой функции f найдется формула А, представляющая функцию f. При этом:
1. Всякая булева функция f ¹ 0 может быть представлена формулой А, находящейся в СДНФ, и такое представление единственно с точностью до порядка следования элементарных конъюнкций.
2. Всякая булева функция f ¹ 1 может быть представлена формулой А, находящейся в СКНФ, и такое представление единственно с точностью до порядка следования элементарных дизъюнкций.
Замечание
- Совершенные нормальные формы булевых функций строятся по тем же правилам, что и совершенные нормальные формы формул алгебры высказываний (конъюнкция при этом обозначается знаком «×»).
- Разложения (2) и (3) – это соответственно ДНФ и КНФ заданной булевой функции f(х1,х2,…,хn).
Пример 1. Найти СДНФ и СКНФ функции f(х,у,z), заданной таблицей истинности:
| х | у | z | f(х,у,z) | ЭК и ЭД |
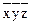
| ||||

| ||||

| ||||

| ||||

| ||||

| ||||

| ||||
| хуz |
|
|
|

Пример 2. Найти СДНФ для булевой функции, заданной формулой 
Решение

Вопрос 4. Принцип двойственности для булевых функций. Самодвойственные функции
О.4.1. Булева функция f*(х1,х2,…,хn) называется двойственной функцией для булевой функции
f(х1,х2,…,хn), если для любых х1,х2,…,хn:
 .
.
Правила построения двойственных функций
Правило №1 (по формуле)
При построении двойственной функции f* по формуле исходной функции f необходимо на место каждой переменной поставить ее отрицание и взять отрицание от всей функции.
Пример 3. Найдем двойственную функцию для функции f = х Ù у:
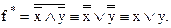
Таким образом, (х Ù у)*= х Ú у.
Аналогично можно показать, что (х Ú у)*= х Ù у.
Следовательно, операции Ú и Ù двойственны друг другу.
Правило №2 (по таблице истинности)
При построении двойственной функции f* по таблице истинности исходной функции f сначала строят функцию  а затем записывают ее значения в обратном порядке. Это и будет таблица истинности двойственной функции f*.
а затем записывают ее значения в обратном порядке. Это и будет таблица истинности двойственной функции f*.
Пример 4.
| х1 | х2 | х3 | f(х1,х2,х3) | 
| f*(х1,х2,х3) |
 0 0
| |||||
Из определения двойственности следует, что
f** = (f*)* = f,
т.е. функция f является двойственной к f* (свойство взаимности).
Т.4.1. (принцип двойственности)
Функция, двойственная суперпозиции функций, равносильна соответствующей суперпозиции двойственных функций, т.е.

Принцип двойственности удобен при нахождении двойственных функций, представленных формулами, содержащими лишь операции конъюнкции, дизъюнкции и отрицания. В этом случае в исходной формуле конъюнкции заменяются на дизъюнкции, а дизъюнкции – на конъюнкции. Т.о., ДНФ соответствует КНФ, КНФ – ДНФ, СДНФ – СКНФ, СКНФ – СДНФ.
|
|
|
Пример 5. 
Т.4.2. Если для функции f(х1,х2,…,хn) двойственной является функция f*(х1,х2,…,хn), то справедлива равносильность 
Самодвойственные функции
О.4.2. Булева функция f(х1,х2,…,хn) называется самодвойственной, если
f*(х1 х2 … хn) = f (х1,х2,…,хn).
Класс самодвойственных булевых функций обозначается буквой S.
Пример 6.
1. Функция f(х) = х является самодвойственной, так как 
2. Функция  является самодвойственной, так как
является самодвойственной, так как 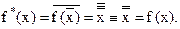
|
|
|


