 |
Сетевые модели в управлении проектами: понятие, основные элементы, критический путь, расчет временных параметров.
|
|
|
|
Сетевая модель – разновидность ориентированного графа, совокупность взаимосвязанных работ и событий, отражающих процесс достижения определенной цели.
Работа (операция, действие) – материальное действие (требуют ресурсов), или логическое действие (требуют взаимосвязи событий), либо процессы, которые устанавливают логическую взаимосвязь.
Событие – результат выполнения одной или нескольких работ и имеет продолжительность.
Путь – любой маршрут последовательных работ. Полные пути связывают исходные и завершающие события сетевой модели. Все остальные пути неполные.
Критический путь – наибольший по продолжительности путь.
В сетевой модели роль вершин графа могут играть события, определяющие начало и окончание отдельных работ, а дуги в этом случае будут соответствовать работам. Такую сетевую модель принято называть сетевой моделью с работами на дугах. В то же время, возможно, что в сетевой модели роль вершин графа играют работы, а дуги отображают соответствие между окончанием одной работы и началом другой. Такую сетевую модель принято называть сетевой моделью с работами в узлах.
Сетевая модель может быть представлена: 1) сетевым графиком, 2) в табличной форме, 3) в матричной форме, 4) в форме диаграммы на шкале времени.
Преимущество сетевых графиков и временных диаграмм перед табличной и матричной формами представления состоит в их наглядности. Однако это преимущество исчезает прямо пропорционально тому, как увеличиваются размеры сетевой модели. Для реальных задач сетевого моделирования, в которых речь идет о тысячах работ и событий, вычерчивание сетевых графиков и диаграмм теряет всякий смысл.
Преимущество табличной и матричной формы перед графическими представлениями состоит в том, что с их помощью удобно осуществлять анализ параметров сетевых моделей; в этих формах применимы алгоритмические процедуры анализа, выполнение которых не требует наглядного отображения модели на плоскости.
|
|
|
Сетевым графиком называется полное графическое отображение структуры сетевой модели на плоскости.
Если сетевым графиком на плоскости отображается сетевая модель типа АоА, то однозначное представление должны получить все работы и все события модели. Однако структура сетевого графика модели АоА может быть более избыточна, чем структура самой отображаемой сетевой модели. Дело в том, что по правилам построения сетевого графика для удобства его анализа необходимо, чтобы два события были соединены только единственной работой, что в принципе не соответствует реальным обстоятельствам в окружающей нас действительности. Поэтому принято вводить в структуру сетевого графика элемент, которого нет ни в действительности, ни в сетевой модели. Этот элемент называется фиктивной работой. Таким образом, структура сетевого графика образуется из трех типов элементов (в отличие от структуры сетевой модели, где только два типа элементов):
· событий – моментов времени, когда происходит начало или окончание выполнения какой-либо работы (работ);
· работ – неделимых частей комплекса действий, необходимых для решения некоторой задачи;
· фиктивных работ – условных элементов структуры сетевого графика, используемых исключительно для указания логической связи отдельных событий.
Графически события изображаются кружками, разделенными на три равных сегмента (радиусами под углом в 120°); работы изображаются сплошными линиями со стрелками на конце, ориентированными слева направо; фиктивные работы изображаются пунктирными линиями со стрелками на конце, ориентированными слева направо. Пример сетевого графика модели АоА представлен ниже на рис. 1.
|
|
|
Отметим, что индексация работ производится рядом с соответствующими стрелками; фиктивные работы не индексируются; индексы событий проставляются в нижнем сегменте соответствующего кружка. Заполнение остальных сегментов рассматривается ниже.
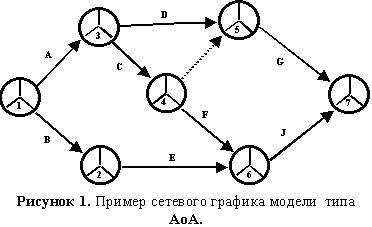
Правило построения сетевого графика модели типа АоА:
1-график строится от исходного события к завершающему (одно событие – начало, и одно – окончание) направление стрелок слева направо
2-все работы, все события д.б. однозначно представлены
3-два события д.б. соединены только единственной работой
4-длина и наклон стрелок значения не имеют, но они д.б. однонаправленными
5-в сети не д.б. замкнутых контуров
6-следует избегать пересечения стрелок
7-события номеруются, начиная с 1. Номер предшествующего д.б. меньше последующего
Различаются следующие разновидности событий сетевого графика модели АоА:
· исходное событие – результат, в отношении которого условно предполагается, что он не имеет предшествующих работ;
· завершающее событие – результат, в отношении которого предполагается, что за ним не следует ни одна работа; это и является конечной целью выполнения всего комплекса работ или решением задачи;
· промежуточное событие или просто событие. Это любой достигаемый результат в выполнении одной или нескольких работ, дающий возможность начать последующие работы;
· начальное событие – событие, непосредственно предшествующее данной конкретной работе;
· конечное событие – событие, непосредственно следующее за данной работой.
Временные параметры (или временные характеристики) сетевой модели являются главными элементами аналитической системы проектного управления. Именно для их определения и последующего улучшения выполняется вся подготовительная, вспомогательная работа по составлению сетевой модели проекта и ее последующей оптимизации.
Различают следующие временные параметры:
· продолжительность работ;
· раннее время начала работы;
· раннее время окончания работы;
· позднее время начала работы;
· позднее время окончания работы;
· раннее время наступления события;
|
|
|
· позднее время наступления события;
· продолжительность критического пути;
· резерв времени наступления события;
· полный резерв времени выполнения работы;
· свободный резерв времени выполнения работы;
· независимый резерв времени выполнения работы.
Продолжительность работы (ti) – календарное время, которое занимает выполнение работы.
Раннее время начала работы (ESTi) – наиболее ранний из возможных сроков начала выполнения работы.
Раннее время окончания работы (EFTi) – равно раннему времени начала работы плюс ее продолжительность.
Позднее время окончания работы (LFTi) – наиболее поздний из допустимых сроков окончания работы.
Позднее время начала работы (LSTi) – равно позднему времени окончания работы минус ее продолжительность.
Раннее время наступления события (EETj) – характеризует наиболее ранний из возможных сроков свершения того или иного события. Поскольку каждое событие является результатом свершения одной или нескольких работ, а те в свою очередь следуют за какими-либо предшествующими событиями, то срок его наступления определяется величиной наиболее длительного отрезка пути от исходного события до рассматриваемого.
Позднее время наступления события (LETj) – характеризует наиболее поздний из допустимых сроков совершения того или иного события. Если установлен срок наступления завершающего события, являющегося результатом всего комплекса проводимых работ, то каждое промежуточное событие должно наступить не позже определенного срока. Этот срок и является предельно допускаемым сроком наступления события.
Любая последовательность непосредственно следующих друг за другом работ в сетевой модели называется путем. Путей в сетевой модели может быть очень много, но при этом пути, связывающие исходное и завершающее события сетевой модели, называются полными, а все остальные – неполными. Сумма продолжительностей выполнения работ, составляющих тот или иной путь, называется продолжительностью этого пути.
Самый продолжительный из всех полных путей называется критическим путем сетевой модели. Таким образом, продолжительность критического пути равна сумме продолжительностей всех работ, составляющих этот путь.
|
|
|
Работы, лежащие на критическом пути, называются критическими работами, а события – критическими событиями.
Уже одного определения критического пути сетевой модели проекта достаточно для организации управления всем комплексом работ. Жестко контролируя календарные сроки выполнения критических работ, можно в итоге избежать потерь. У работ, не находящихся на критическом пути, как правило, имеются резервы времени, позволяющие на некоторое время откладывать их выполнение, если это необходимо.
Резерв времени наступления события – это разница между поздним и ранним сроками наступления этого события.
Полный резерв времени выполнения работы (TFi) – это максимально возможный запас времени для выполнения данной работы сверх продолжительности самой работы при условии, что в результате такой задержки конечное для данной работы событие наступит не позднее, чем в свой поздний срок.
Сумм РВ=ПВО-РВН-прод-ть
Свободный резерв времени выполнения работы (FFi) – это запас времени, которым можно располагать при выполнении данной работы в предположении, что предшествующее и последующее события этой работы наступают в свои самые ранние сроки.
Своб.рез.вр=РВНслед.раб – РВН – прод-ть
Независимый резерв времени выполнения работы (IFi) – это запас времени, на который можно отложить начало выполнения работы без риска повлиять на какие бы то ни было сроки наступления каких-либо событий в модели вообще.
Нез=РВНслед.раб – ПВН – прод-ть
Правила расчета раннего и позднего времени наступления события:
1) Проход вперед: РВ=0
РВО=РВН+прод-ть
Если событие является окончанием для нескольких работ, то рассчитывается РВ по каждому пути, и берется мах
2) Проход назад: ПВ=РВ, ПВН=ПВО-прод-ть, мin.
Если одно событие является началом для нескольких работ, то рассчитывается позднее время по каждому и берется мин.
На основании значений раннего и позднего времени событий можно определить критич путь. Признаки критич работ: РВН=ПВН, РВО=ПВО, ВН+прод-ть=ВО
|
|
|


