 |
Особенности вычитания двоично-десятичных чисел.
|
|
|
|
По аналогии с операциями вычитания в двоичном коде, операцию X-Y можно представить как X + (-Y). При этом отрицательное число представляется в дополнительном коде, аналогичном дополнительному коду в двоичной арифметике. Этот код используется только для выполнения операций вычитания.
Алгоритм выполнения операции состоит в следующем:
1) Модуль положительного числа представляется в прямом двоично-десятичном коде (8421).
Модуль отрицательного числа - в дополнительном коде (ДК) с избытком 6.
Для получения ДК необходимо:
- инвертировать значения разрядов всех тетрад числа;
- к младшему разряду младшей тетрады прибавить 1.
Таким образом, цепочка ПК(mod) ® ОК ® ОК+1 ® ДК аналогична цепочке в двоичной арифметике. Только здесь получается ДК с избытком 6, т.к. дополнение идет не до 10, а до 16.
2) Произвести сложение операндов (X) в ПК и (Y) в ДК.
3) Если при сложении тетрад возник перенос из старшей тетрады, то он отбрасывается, а результату присваивается знак "+", т.е. результат получается в прямом избыточном коде. Он корректируется по тем же правилам, что и при сложении модулей.
4) Если при сложении тетрад не возникает переноса из старшей тетрады, то результату присваивается знак "-", т.е. результат получается в избыточном ДК. В этом случае необходимо перейти к избыточному ПК (т.е. инвертировать все двоичные разряды двоично-десятичного числа и прибавить к младшему разряду 1).
5) Полученный в этом случае результат в ПК корректируется. Для этого к тем тетрадам, из которых возникал перенос при выполнении пункта 2 (при суммировании) необходимо добавить 10(10) или 1010(2). Возникшие при этом межтетрадные переносы не учитываются. Таким образом, корректировка происходит в тех тетрадах, которые в положительных числах не корректируются.
|
|
|
Пример 1:
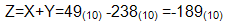 |  | ||
Представим |Y| в ДК с избытком 6:

Выполним сложение:

Отсутствие переноса из старшей тетрады является признаком того, что результат получился в ДК (т.е. отрицательный).
Перейдем к нескорректированному избыточному ПК.

Особенности вычитания двоично-десятичных чисел (прдлж).
Произведем коррекцию результата в соответствии с пунктом 5 алгоритма.

Поскольку ранее результат получался в ДК, т.е. отрицательный, необходимо добавить знак (-). Окончательный результат будет следующий: 
Особенности вычитания двоично-десятичных чисел (прдлж).
Пример 2:
Z=X-Y=143(10) -58(10) =85(10) 
Представим |Y| в ДК с избытком 6:

Выполним сложение:

Наличие переноса из старшей тетрады указывает на то, что результат получился в ПК (т.е. положительный).
Произведем коррекцию результата в соответствии с пунктом 3 алгоритма:

Умножение модулей двоично-десятичных чисел.
Операция умножения сводится к образованию и многократному сложению частичных двоично-десятичных произведений.
Алгоритм умножения:
1. Сумма частичных произведений полагается равной нулю.
2. Анализируется очередная тетрада множителя и множимое прибавляется к сумме частичных произведений столько раз, какова цифра, определяемая этой тетрадой.
3. Сумма частичных произведений сдвигается на одну тетраду и повторяются действия, указанные в пункте 2, пока все цифры (тетрады) множителя не будут обработаны. Направление сдвига зависит от того, какой вариант перемножения выбран - "старшие разряды вперед" или "младшие разряды вперед".
4. Каждая операция суммирования завершается десятичной коррекцией, соответствующей случаю суммирования двоично-десятичных чисел без избытка 6 (т.е. необходимо добавить 0110 к тем тетрадам, из которых был перенос или в которых f=1).
|
|
|
|
|
|


