Физические основы процесса диффузии

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное

учреждение высшего профессионального образования

«Юго-Западный государственный университет»

(ЮЗГУ)

 

Кафедра вычислительной техники

 

УТВЕРЖДАЮ Проректор по учебной работе ____________ О.Г. Локтионова «___» ___________ 2014 г.

 

 

МОДЕЛИРОВАНИЕ ДИФФУЗИОННОГО ПРОФИЛЯ ЛЕГИРУЮЩЕЙ ПРИМЕСЕЙ В КРЕМНИИ

 

Методические указания по выполнению лабораторной работы по дисциплине

«Технология производства электронных средств»

для студентов направления подготовки бакалавров 210200.62

 

Курск 2014

УДК 621.793

 

Составители: В.В.Умрихин

 

Рецензент

Кандидат физико-математических наук А. В. Кочура

 

Моделирование диффузионного профиля легирующей примеси в кремнии: методические указания по выполнению лабораторной работы по дисциплине «Технология производства электронных средств» / Юго-Зап. гос. ун-т; сост.: В.В.Умрихин. Курск, 2014. 15 с.: ил. 3, прилож. 1. Библиогр.: с. 14.

 

Содержат сведения по расчету профиля ле­гирующих примесей в кремнии при диффузии из постоянного источника и из слоя конеч­ной толщины в полуограниченное тело. Указывается порядок выполнения лабораторной работы.

Предназначены для студентов направления подготовки бакалавров 210200.62.

 

Текст печатается в авторской редакции

 

Подписано в печать. Формат 60 84 1/16.

Усл. печ. л.. Уч.-изд. л.. Тираж экз. Заказ. Бесплатно.

Юго-Западный государственный университет.

305040, г. Курск, ул. 50 лет Октября, 94

ЦЕЛЬ РАБОТЫ

 

Изучить физические основы процесса диффузии и методику рас­чета диф­фузионных профилей при диффузии из постоянного источника и слоя конечной толщины в полуограниченное тело.

 

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

 

Физические основы процесса диффузии

 

В реальной кристаллической решетке атомы при определенных условиях могут обладать большой свободой передвижения и переме­щаться из одних уз­лов решетки в другие. Перенос вещества, обус­ловленный хаотическим тепло­вым движением атомов, в направлении уменьшения их концентрации называ­ется диффузией. Диффузия в крис­талле, находящемся в состоянии химического равновесия (однород­ный химический состав, однородное распределение дефек­тов), назы­вается самодиффузией. Диффузия атомов в кристалле при наличии градиента химического потенциала (градиента концентрации вещест­ва) носит название гетеродиффузии, химической диффузии или просто диффузии.

Диффузия атомов в кристаллической решетке осуществляется от­дельными скачками из одного положения равновесия в другое. Длина таких элементарных перемещений имеет порядок постоянной решетки, т.е. несколько десятых долей нанометра. За счет таких элементарных скачков атомы могут перемещаться на большие расстояния. Возможны три механизма атомных скачков: взаимный обмен местами, движение по вакансиям и перемещение по междоузлиям.

Пер­вый механизм может осуществляться при одновременном обмене местами двух, трех (и бо­лее) соседних атомов. Обмен местами двух соседних атомов яв­ляется простейшим актом диффузии (рис.2.1, а). Однако при этом в плотно упа­кованной структуре атом должен преодолеть большой потенциаль­ный барьер, что обусловлено необходимостью смещения соседних ато­мов. При кольцевом обмене (рис.2.1, б) три, четыре или большее число атомов согласованно пере­мещаются на одно межатомное рассто­яние. При таком перемещении потенци­альный барьер, преодолеваемый каждым атомом, меньше, чем в первом случае. Однако вероятность осуществления такого диффузионного механизма умень­шается с увели­чением числа атомов в кольце за счет возрастания суммарной энер­гии, затрачиваемой на элементарный акт перемещения. Диффузионные процессы, обусловленные механизмом атомных скачков, могут проте­кать в со­вершенных кристаллических решетках с рыхлой упаковкой.

Диффузия по вакансиям происходит следующим образом: вначале в ре­шетке образуются вакансии, затем они последовательно переме­шаются по кри­сталлу (рис.2.2, а).

При диффузии атомов по междоузлиям происходят перескок атома из узла решетки в междоузлие и последующие перемещения его уже только по ним (рис.2.2, б).

Эти два механизма диффузии наиболее вероятны в реальных кристаллах с большой концентрацией дефектов. Модели механизмов диффузии атомов по вакансиям и междоузлиям были предложены Я. И. Френкелем в 1926 г. В рам­ках кинетической теории кристаллов, развитой Я. И. Френкелем, эти меха­низмы можно представить следующим образом. Атомы, находящиеся в узлах кристаллической решетки, на­ходятся в непрерывном тепловом движении около центра равновесия. Часть из них приобретает энергию, достаточную для пре­одоления по­тенциального барьера, удерживающего их в положении равнове­сия. Такие атомы переходят из положения равновесия в узле решетки в нерав­новесное положение в междоузлии. При этом образуется дефект по Френкелю (атом в междоузлии и пустой узел - вакансия).

Наряду с дефектами по Френкелю в кристаллической решетке мо­гут обра­зовываться только вакансии - дефекты по Шоттки. Они воз­никают при выбросе за счет тепловых колебаний одного из поверх­ностных атомов из положения равновесия так, что он сохраняет с кристаллом только частичную связь (адсор­бированное состояние).

Вакансии, образующиеся за счет дефектов по Френкелю и по Шоттки, в результате тепловых колебаний могут быть легко замещены соседними ато­мами, что приводит к их перемещению по узлам крис­таллической решетки. В кристалле при тепловом равновесии содер­жится определенное количество ва­кансий. Их концентрация увеличивается с температурой по экспоненциальному закону:

, (2.1)

где - энергия, затрачиваемая на образование вакансии; эВ/град - постоянная Больцмана; T – температура кристалла.

 

а)	б)
Рис.2.1. Механизм диффузии при обмене местами атомов

 

Концентрация равновесных вакансий в кристаллических решетках герма­ния и кремния при комнатной температуре составляет м^-3 и увели­чивается с повышением температуры, а также при возрастании концентрации примесей и дефектности решетки. Так, в условиях термодинамического равно­весия в кремнии при температурах 1273 - 1473 К м^-3.

 

а)	б)
Рис.2.2.Механизм диффузии атомов по вакансиям и междоузлиям

При достижении концентрацией значения м^-3 (т.е., ког­да коли­чество вакансий приближается к % от количества узлов) кристалл пла­вится.

Внедренные в междоузлия атомы могут относительно легко пере­мещаться по ним, так как они связаны с решеткой слабее, чем ато­мы, находящиеся в уз­лах. За счет этого атомы в решетке с дефекта­ми могут обладать достаточно вы­сокой подвижностью. Скорость пере­мещения атомов, выраженная как вероят­ность их перехода из одного равновесного положения в другое вследствие ста­тистического харак­тера процесса, возрастает с повышением температуры по экспоненци­альному закону:

(2.2)

где - потенциальный барьер (энергия активации), преодолеваемый атомом при переходе из одного положения равновесия в другое, вы­сота которого опре­деляется характером химической связи атомов в кристалле и механизмом диф­фузии.

Среднее время нахождения атома в одном из положений равнове­сия

. (2.3)

Здесь - постоянная, соизмеримая с периодом собственных колеба­ний атомов в узлах решетки (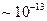 с).

Для определения коэффициента диффузии в твердом теле можно восполь­зоваться выражением для коэффициента диффузии, полученным из кинети­ческой теории газов. В отличие от газов элементарные перемещения атомов в кристаллах осуществляются на постоянное расстояние, равное или кратное пе­риоду решетки а, поэтому коэффициент диффузии в кристалле

, (2.4)

где - коэффициент, зависящий от структуры кристалла и механиз­ма диф­фузии.

Для объемно-центрированной кубической решетки при диффузии по ва­кансиям , а при диффузии по междоузлиям .

С учетом (2.4) выражение для коэффициента диффузии может быть пред­ставлено в виде

, (2.5)

где .

Выражение (2.5) справедливо для процессов самодиффузии и диффузии, примесных атомов, как по вакансиям, так и по междоузлиям кристаллической решетки.

Механизмы диффузии различных элементов определяются главным обра­зом типом твердого раствора, который они образуют в кристал­лической ре­шетке, т.е. тем, располагаются ли примесные атомы в узлах или междоузлиях кристаллической решетки (твердые растворы замещения или внедрения соот­ветственно) или образуют растворы смешанного типа (атомы размещаются по узлам и междоузлиям).

При диффузии примесных атомов по вакансиям одновременно про­текает процесс самодиффузии. Однако этот процесс идет значительно медленнее, так как химическая связь между атомами вещества силь­нее связи примесных ато­мов с решеткой.

Механизмы диффузии примесных атомов в кристаллической решет­ке при изменении температуры и концентрации примеси может изме­няться. В проме­жуточной переходной области возможна диффузия по обоим механизмам. При изменении механизма диффузии изменяются и параметры .

Существенное влияние на скорость диффузии оказывают атомы примеси и другие дефекты, присутствующие в кристалле. Локальная деформация решетки вблизи примесного атома приводит к уменьшении энергии связи между сосед­ними атомами, что увеличивает вероят­ность образования вакансий. При вакан­сионном механизме диффузии это приводит к увеличению скорости диффузии. Энергия активации процесса диффузии может изменяться также вследствие ку­лоновского взаимодействия между атомами диффузанта и присутствующей в решет­ке примеси. Так, в германии и кремнии наличие акцепторной примеси ускоряет, а наличие донорной примеси замедляет процесс диффузии атомов донора.

Скорость диффузии примесей в полупроводниках обратно пропор­цио­нальна их предельной растворимости. Высокая растворимость при­месей на­блюдается в случае образования твердых растворов замеще­ния. В случае, когда атомы примесей в силу их слабой связи с ре­шеткой не могут замещать узлы, образуются твердые растворы внед­рения, область растворимости сужается, так как в междоузельном пространстве может разместиться меньшее количество атомов. Ско­рость же диффузии примесей по междоузлиям значительно выше ско­рости диффузии по вакансиям решетки.

Основные диффузионные параметры ряда примесей в кремнии при­ведены в табл.П.1.

Диффузионный профиль

 

Законы Фика

 

При диффузии, обусловленной только градиентом концентрации, выраже­ние для потока диффундирующего вещества (примеси) имеет следующий вид:

, (2.6)

где J - вектор плотности потока диффундирующего вещества; D - ко­эффи­циент диффузии; N - концентрация атомов диффундирующего ве­щества.

Знак минус в выражении (2.6) указывает, что диффузионный пе­ренос ве­щества происходит в направлении уменьшения концентрации примеси.

Когда концентрация вещества изменяется лишь в направлении оси X, по­ток

. (2.7)

Здесь dN/dx - градиент концентрации диффундирующего вещества.

Выражение для скорости накопления диффундирующего вещества может быть получено из (2.6) и принципа сохранения, согласно ко­торому изме­нение концентрации вещества в определенном объеме должно быть равно со­ответствующему потоку его в данный объем:

. (2.8)

При подстановке (2.7) в (2.8) получаем для одномерного случая

. (2.9)

Когда коэффициент диффузии можно считать постоянным, выра­жение (2.9) может быть записано как

. (2.10)

Выражения (2.6) – (2.10) впервые были получены в 1885 г. швейцарским ученым Фиком для описания диффузионных процессов в идеальных газах и растворах. В дальнейшем была показана примени­мость установленных законов для описания процессов диффузии в твердых телах. Уравнения (2.6) и (2.10) носят названия первого и второго законов Фика соответственно.

На основании этих законов при заданных начальных и граничных усло­виях, а также при известном коэффициенте диффузии могут быть решены за­дачи нахождения: распределения примеси, потока вещества через заданную по­верхность, количества продиффундировавшего ве­щества и др.

 

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: