Решение уравнения диффузии для неограниченного тела

 

Решение уравнения диффузии для неограниченного тела при заданном в общем виде начальном распределении примесей

(2.11)

находят методом разделения переменных. Если концентрацию N(x,t) пред­ста­вить как произведение двух функций, каждая из которых за­висит только от од­ной переменной , то выражение (2.10) принимает вид

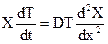(2.12)

или

(2.13)

Так как левая часть равенства (2.13) не зависит от х, а пра­вая - от t, то они должны быть тождественно равны некоторой пос­тоянной отрицательной вели­чине (будет показано далее), которую обозначим .

В результате получим дифференциальные уравнения

(2.14)

решения которых имеют вид

(2.15)

Из (2.15) очевидно, что показатель экспоненты должен быть отрицатель­ным, в противном случае концентрация вещества со временем будет неограни­ченно возрастать.

Таким образом, концентрация

(2.16)

или

(2.17)

Здесь

После преобразований с учетом граничных условий общее реше­ние урав­нения диффузии для неограниченного изотропного тела может быть записано в виде

. (2.18)

Наиболее часто при расчете распределения концентрации приме­си прихо­дится решать уравнения диффузии в тело, ограниченное плоскостью x = 0.

Диффузия из постоянного источника в

Полуограниченное тело

 

Гра­ничные условия для этого случая

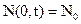, . (2.19)

Решение уравнения диффузии для этого случая имеет вид:

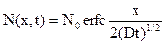, (2.20)

где символ erfc означает дополнение (до единицы) функции ошибок. Ве­ли­чину , имеющую размерность длины, называют диффузион­ной дли­ной. Значения для дополнения функции ошибок

(2.21)

вычисляются в программе Mathcad.

Из выражения (2.20) следует, что заданное распределение примеси можно получить при различных сочетаниях значений D (зависит от температуры Т) и времени t. Кроме того, величина температурно-времен­ного воздействия определяет при постоянной концентрации ко­личество примеси, введенное в кристалл, т.е. дозу легирования (рис. 2.1)

 

Рис.2.3. Распределение диффундирующей примеси по глубине из постоянного внешнего источника

 

Дозу легирования Q, т.е. число атомов примеси, введенное в кристалл во время диффузии через площадку в 1 см², можно получить на основе первого закона Фика (2.7). Подставляя вместо N его зна­чение из (2.20), получим

. (2.22)

Интегрируя полученное выражение по времени, найдем

, (2.23)

Диффузия из неограниченного источника является реальным случаем в производстве ИС и представляет собой первый этап диффузии, задачей кото­рого является введение в кристалл определенного коли­чества примеси. В ре­зультате образуется тонкий приповерхностный слой, насыщенный примесью. В производстве этот этап нередко назы­вают загонкой примеси.

При проведении последовательной диффузии донорной примеси в полу­проводник р -типа, однородно легированный акцепторной примесью N_a, сум­марное распределение электрически активных примесей

. (2.24)

Точка х_и, в которой концентрации донорной и акцепторной примесей равны, называется точкой инверсии типа проводимости (т.е. область, где N(x,t) > N_a, будет n -типа, а где N(x,t) < N_a - р -типа).

 

Диффузия из бесконечно тонкого слоя в

полуограниченное тело с от­ражающей границей

 

Решение уравнения диффузии для этого случая имеет вид (распределение Гаусса)

, (2.25)

где Q- доза легирования, см^-2.

В производстве этот этап после загонки примеси называют раз­гонкой. В совокупности эти два этапа называют двухстадийиой диф­фузией. При проведе­нии разгонки донорной примеси в полупроводнике р -типа, однородно легиро­ванным акцепторной примесью N_a, суммарное распределение электрически ак­тивных примесей описывается выраже­нием

. (2.26)

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

 

1.В соответствии с заданным вариантом (табл.П1) построить профили рас­пределения примесей при загонке (Т_з =1000°С) и разгонке.

2. Найти координаты точек инверсии х_и типа проводимости и на­нести их на графики.

3. Определить дозу легирования Q при загонке.

 

Примечание. 1. Исходная концентрация примеси в объеме кристалла см^-3.

2. Исходные данные вариантов для расчета приведены в табл.П1.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

 

1. Что называется диффузией?

2. Механизмы диффузии в твердом теле.

3. Дефекты по Френкелю и Шоттки в кристаллической решетке.

4. Температурная зависимость концентрации вакансий в объеме твердого тела.

5. Коэффициент диффузии и энергия активации.

6. Параметры, влияющие на скорость диффузии.

7. Законы Фика.

8. Решение уравнения диффузии для неограниченного тела.

9. Диффузия из постоянного источника.

10. Диффузия из бесконечно тонкого слоя.

11. Применение диффузии для создания р-n – переходов.

 

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

 

1. Пичугин И.Г., Таиров Ю.М. Технология полупроводниковых приборов. М.: Высшая школа, 1984. 288 с.

2. Парфенов О.Д. Технология микросхем. М.: Высшая школа, 1977. 256 с.

3. Черняев В. К. Физико-химические процессы в технологии РЭА. М.: Высшая школа. 376 с.

 

ПРИЛОЖЕНИЕ

Таблица П.1

Исходные данные для расчета

 

№ вар	Элемент	D0, м2/с	ΔЕ, эВ	N0, см–3 при Тз=1000оС	tзаг, мин	tр, мин	Тр, оС
	As	3,2·10–5	3,6	2,1·1021
	В	8,2·10–4	3,7	4,0·1020
	Р	1,1·10–3	3,7	1,0·1021
	Ga	3,6·10–4	4,1	3,0·1019
	Sb	5,6·10–4	3,9	4,0·1019
	Al	6,2·10–4	3,3	8,0·1019
	As	3,2·10–5	3,6	2,1·1021
	В	8,2·10–4	3,7	4,0·1020
	Р	1,1·10–3	3,7	1,0·1021
	Ga	3,6·10–4	4,1	3,0·1019
	Sb	5,6·10–4	3,9	4,0·1019
	Al	6,2·10–4	3,3	8,0·1019
	As	3,2·10–5	3,6	2,1·1021
	В	8,2·10–4	3,7	4,0·1020
	Р	1,1·10–3	3,7	1,0·1021
	Ga	3,6·10–4	4,1	3,0·1019
	Sb	5,6·10–4	3,9	4,0·1019
	Al	6,2·10–4	3,3	8,0·1019
	As	3,2·10–5	3,6	2,1·1021
	В	8,2·10–4	3,7	4,0·1020
	Р	1,1·10–3	3,7	1,0·1021
	Ga	3,6·10–4	4,1	3,0·1019
	Sb	5,6·10–4	3,9	4,0·1019
	Al	6,2·10–4	3,3	8,0·1019
	As	3,2·10–5	3,6	2,1·1021
	В	8,2·10–4	3,7	4,0·1020
	Р	1,1·10–3	3,7	1,0·1021
	Ga	3,6·10–4	4,1	3,0·1019
	Sb	5,6·10–4	3,9	4,0·1019
	Al	6,2·10–4	3,3	8,0·1019

 

Примечание. t_з - время загонки примеси; t_p - время разгонки примеси; T_p - температура разгонки примеси; ΔE - энергия активации; N₀ - предельная растворимость примеси в кремнии, см^–3.

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: