 |
Методы расчета случайных погрешностей
|
|
|
|
Методы расчета случайных погрешностей
1. Для прямых измерений.
Пусть при измерениях возникают только случайные погрешности, систематические погрешности настолько малы, что ими можно пренебречь, а грубые ошибки отсутствуют.
Тогда, измеряя несколько раз величину  , мы получаем серию значений
, мы получаем серию значений  . Каждое из измеренных значений содержит случайную погрешность
. Каждое из измеренных значений содержит случайную погрешность
 (
(  ) (8)
) (8)
Поскольку истинное значение  неизвестно, то остаются неизвестными по величине и знаку случайные погрешности, возникающие при каждом измерении, поэтому для учета максимально возможной погрешности разность
неизвестно, то остаются неизвестными по величине и знаку случайные погрешности, возникающие при каждом измерении, поэтому для учета максимально возможной погрешности разность  берется по модулю.
берется по модулю.
Теория показывает, что близким к истинному значению измеряемой величины является среднее арифметическое ряда отдельных измерений:
 (9)
(9)
где  – число повторных измерений.
– число повторных измерений.
Среднее значение в данном методе используется как действительное, поэтому данный метод расчета погрешностей получил название метода среднего арифметического или метода среднего значения.
Находя для каждого измерения 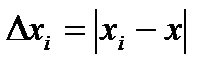 , аналогично (9) находим
, аналогично (9) находим 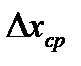 :
:

В теории погрешностей доказывается, что при увеличении числа  случайная погрешность среднего арифметического
случайная погрешность среднего арифметического  стремится к нулю и может быть использована в качестве оценочного значения абсолютной погрешности. Окончательный результат измерений записывается в виде:
стремится к нулю и может быть использована в качестве оценочного значения абсолютной погрешности. Окончательный результат измерений записывается в виде:
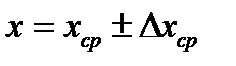 (10)
(10)
с указанием под результатом величины средней относительной погрешности. Средняя относительная погрешность определяется выражением:
 (11)
(11)
При измерениях встречаются такие ситуации, когда случайные погрешности настолько малы, что повторные измерения дают значения, попадающие в пределы интервала погрешности прибора. В этом случае погрешность измерений можно взять из паспорта прибора. Если паспорт отсутствует, расчет погрешности производится по классу точности прибора (формула 7), а если класс точности не указан, то значение абсолютной погрешности принимают равным половине цены наименьшего деления шкалы прибора.
|
|
|
Для электронных приборов при отсутствии паспорта и неизвестном классе точности приборная погрешность принимается равной дискретности прибора на данном пределе измерения. Дискретность можно определить даже при нулевых показаниях включенного прибора. Например, электронный прибор включен на так, что на табло светятся цифры 0. 000, следовательно, дискретность равна 0, 001. Если прибор показывает 0. 00, дискретность равна 0, 01. При показаниях 00. 0, дискретность 0, 1.
В случае однократных измерений в качестве абсолютной погрешности тоже используется приборная погрешность. В любом случае, результирующая погрешность не может быть равной нулю. Если она таковой оказывается, то это является либо следствием неправильно выбранного для данного измерения метода расчета погрешностей, либо ошибки в расчетах.
2. Для косвенных измерений.
При косвенных измерениях искомую физическую величину  определяют путем вычислений по результатам прямых измерений других величин. Для оценки погрешностей косвенных измерений величины
определяют путем вычислений по результатам прямых измерений других величин. Для оценки погрешностей косвенных измерений величины  необходимо вывести формулу для ее относительной погрешности
необходимо вывести формулу для ее относительной погрешности  . Пусть искомая величина является функцией нескольких переменных:
. Пусть искомая величина является функцией нескольких переменных:
 (12)
(12)
Тогда для расчета погрешности измерений можно использовать дифференциальный (другое название логарифмический) метод, в основе которого лежит свойство натурального логарифма:

Полный дифференциал логарифма исходной функции будет равен:
|
|
|
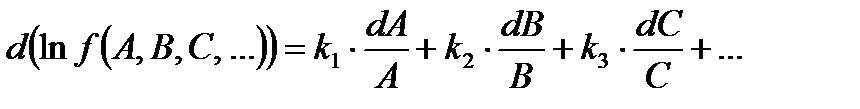
где 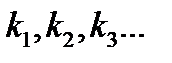 – показатели степени аргументов
– показатели степени аргументов 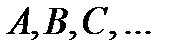
Таким образом, получаем:

Учитывая, что дифференциал независимой переменной равен ее приращению (  ), и если приращение аргумента мало для функции, то дифференциал функции приблизительно равен ее приращению, то есть
), и если приращение аргумента мало для функции, то дифференциал функции приблизительно равен ее приращению, то есть  , получаем:
, получаем:

Значения  измеряют один или несколько раз и обрабатывают по правилам оценки погрешностей прямых измерений. Если при логарифмировании и дифференцировании в выражении появились знаки «–», то для нахождения максимальной относительной погрешности их необходимо заменить на знаки «+».
измеряют один или несколько раз и обрабатывают по правилам оценки погрешностей прямых измерений. Если при логарифмировании и дифференцировании в выражении появились знаки «–», то для нахождения максимальной относительной погрешности их необходимо заменить на знаки «+».
Таким образом, для определения погрешностей косвенных измерений искомой величины  используют формулу, полученную по следующим правилам:
используют формулу, полученную по следующим правилам:
§ взять натуральный логарифм расчетной формулы;
§ продифференцировать полученное выражение;
§ произвести замену знаков дифференциала  на знаки конечного приращения
на знаки конечного приращения  ;
;
§ знаки “минус” заменить знаками “плюс”, так как суммарная погрешность всегда больше погрешности отдельных измерений;
§ в полученную формулу подставить средние арифметические значения измеренных величин и их абсолютные погрешности;
§ рассчитать относительную (Е), а затем абсолютную (Δ Y) погрешности измерений искомой величины;
§ результат измерений записать в виде: 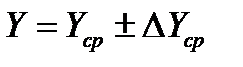 .
.
Пример: Пусть в лабораторной работе требовалось определить удельное сопротивление проволоки с использованием закона Ома. Прямыми измерениями определяются сила тока  , напряжение
, напряжение  , длина
, длина 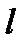 , площадь поперечного сечения проволоки через радиус
, площадь поперечного сечения проволоки через радиус  . Тогда расчетная формула будет иметь вид:
. Тогда расчетная формула будет иметь вид:
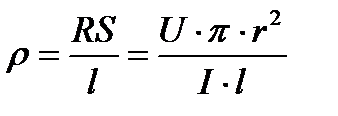
Выведем формулу для расчета погрешностей:
 ;
;

(в данном случае число  принято за постоянную);
принято за постоянную);
 ;
;
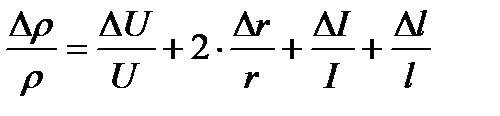 ;
;
 ;
;
 ;
;
результат запишем в виде:

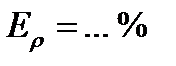 .
.
|
|
|


