 |
Математическая обработка результатов измерений
|
|
|
|
Математическая обработка результатов измерений
Ошибка результата определяется не только неточностями измерений, но и неточностями вычислений. Вычисления необходимо проводить так, чтобы их ошибка была на порядок меньше ошибки результата измерений. Для этого необходимо вспомнить правила математических действий с приближенными числами.
Значащими называются все цифры кроме нуля, стоящего слева от чисел. Нуль, стоящий между значащими цифрами или справа от них, также значащая цифра.
Примеры:
1) 0, 0105. Два нуля слева – не значащие цифры. Всего число имеет три значащих цифры, в том числе и нуль, стоящий между значащими цифрами 1 и 5;
2) 5000. Нули справа – значащие. Всего число имеет четыре значащих цифры (нули получились не в результате округления, а при измерении);
3) 5∙ 103. Число имеет одну значащую цифру, то есть при измерениях учитывались только тысячи. Точность числа 5∙ 103 в тысячу раз меньше 5000.
Правила округления чисел
Если не все числа заканчиваются на одном и том же разряде, то для упрощения действий до их выполнения следует произвести округления до разряда на единицу меньшего, чем разряд наименее точного числа по правилам 1, 2 и 3.
Пример. 
.
Правило 1. Округление достигается простым отбрасыванием цифр, если первая из отбрасываемых цифр меньше, чем 5.
Пример. 0, 234 ≈ 0, 23.
Правило 2. Если первая из отбрасываемых цифр больше, чем 5, то последняя цифра увеличивается на 1. Последняя цифра увеличивается также и в том случае, когда первая из отбрасываемых цифр 5, а за ней есть одна или несколько цифр, отличных от нуля.
Пример. 35, 856 ≈ 35, 9.
Правило 3. Если отбрасываемая цифра равна 5, а за ней нет значащих цифр, то округление производится на ближайшее четное число. Последняя сохраняемая цифра оставляется неизменной, если она четная, и увеличивается на единицу, если она нечетная.
|
|
|
Пример. 0, 0465 ≈ 0, 046; 0, 935 ≈ 0, 94.
При выполнении математических операций также возникает необходимость округления чисел, которое проводится в соответствии с правилами.
1. При сложении и вычитании приближенных чисел следует сохранить столько десятичных знаков, сколько их в приближенном данном с наименьшим числом десятичных знаков:
Пример. 23, 2 + 0, 442 + 7, 247 ≈ 23, 2 + 0, 44 + 7, 25 ≈ 30, 9.
2. При умножении и делении приближенных чисел произведение или частное будет иметь столько значащих цифр, сколько их имеет приближенное данное с наименьшим числом значащих цифр:
Пример. 
;
.
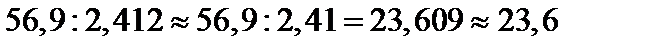3. При возведении в степень в результате сохраняется столько значащих цифр, сколько их имеет возводимое в степень приближенное число:
Пример. 
.
4. При извлечении корня сохраняется столько значащих цифр, сколько их имеет подкоренное выражение:
Пример. 
.
5. При нахождении логарифма из таблиц следует брать столько знаков, сколько значащих цифр содержит данное число:
Пример. 
.
Число значащих цифр окончательного результата определяется порядком величины абсолютной погрешности. Таким образом, результат округляют до того разряда, в котором находится значащая цифра абсолютной ошибки.
Пример. 
, 
, 
.
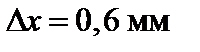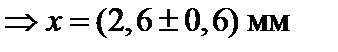Правила построения графиков
Во многих случаях оказывается удобным графически изображать зависимость между изучаемыми величинами. При этом необходимо руководствоваться следующими правилами.
1. При построении графика значения независимой переменной откладываются по горизонтальной оси (оси абсцисс), а значения функции – по вертикальной оси (оси ординат). В качестве независимой переменной или функции может выступать как сама функция, так и какая-либо ее степень или комбинация нескольких физических величин.
|
|
|
Величины, откладываемые по осям, должны указываться вместе со своими единицами измерений.
2. Исходя из пределов изменения независимой переменной и функции, необходимо выбрать независимые друг от друга масштабы по осям. График должен располагаться в центре координатной плоскости или четверти.
3. Для упрощения построения графика удобно на основании измерений составить таблицу, в которой каждому значению независимой переменной соответствует значение функции.
4. Экспериментальные точки наносятся на график с учетом погрешностей. Числовые значения экспериментальных точек и погрешностей на графике не наносятся. Вспомогательные линии для построения графика, например, штрихованные, проводить нельзя, так как они ухудшают наглядность графика.
5. При построении графика следует разумно выбирать масштабы по осям так, чтобы экспериментальные точки располагались по всей координатной плоскости. Для этого, при необходимости, допускается смещение нуля по одной или обеим осям.
6. После построения экспериментальных точек проводится плавная кривая так, чтобы, по возможности, она проходила внутри интервалов погрешности. Следует заранее задуматься о виде кривой (прямая, гипербола, парабола и т. д. ) исходя из известных теоретических представлений (формул).
Если какая-либо точка находится в стороне от проведенного графика, то на нее следует обратить особое внимание, возможно при данном измерении была допущена ошибка. Если это не так, то в районе этой точки искомая зависимость имеет резко выраженную особенность. Такие особенности представляют наибольший интерес. Поэтому необходимо внимательно промерить область вблизи этой точки.
|
| Рис. 1. График зависимости I = f (U) |
Пример. Построим график зависимости силы тока, текущего по проводнику, от напряжения на его концах (рис. 1).
В результате эксперимента получены следующие значения этих величин с соответствующими абсолютными погрешностями:
| № опыта | I, А | Δ I, А | U, В | Δ U, В |
| 0, 19 | 0, 07 | 0, 11 | 0, 02 | |
| 0, 39 | 0, 06 | 0, 21 | 0, 03 | |
| 0, 75 | 0, 08 | 0, 44 | 0, 03 | |
| 1, 28 | 0, 07 | 0, 64 | 0, 04 | |
| 1, 63 | 0, 08 | 0, 84 | 0, 02 |
1. Нарисуем координатную плоскость.
|
|
|
2. Выберем масштаб таким образом, чтобы максимальное значение силы тока было равно 1, 7 А, а максимальное значение напряжения 0, 9 В.
3. Обозначим координатные оси.
4. Нанесем экспериментальные точки с соответствующими погрешностями.
5. Проведем экспериментальную кривую так, чтобы она не выходила за пределы погрешностей.
По графику можно определить численное значение искомой величины и ее абсолютную погрешность.
|
| Рис. 2. Определение абсолютной погрешности графически |
Пример. Определение концентрации C раствора по его оптической плотности D. В этой работе сначала измеряется оптическая плотность нескольких растворов с известной концентрацией 
и на основании данных строится график зависимости D=f(C) (рис. 2). Затем измеряется величина оптической плотности Dx раствора неизвестной концентрации. Пусть она была измерена 3 раза и оказалась равной 0, 76, 0, 78, 0, 75. Среднее значение Dх ср=0, 76, а средняя абсолютная ошибка Δ Dх ср=0, 01. По графику находят значение концентрации Сх ср соответствующее среднему значению Dх ср. В рассмотренном случае Сх ср=1, 42 %. Около значения Dх ср на оси ординат откладывают Δ Dх ср, по графику находят, какой отрезок соответствует ему на другой оси Δ Сх ср. Он равен 0, 02 %. Окончательный результат запишется в виде 
.
|
|
|
