Обработка результатов измерений

Обработка результатов измерений

1. Рассчитайте абсолютные и относительные погрешности микроамперметра и вольтметра для каждого опыта по формулам:

, ,                    (5)

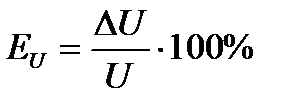, ,       (6)

где k_I и k_U − классы точности приборов (микроамперметра и вольтметра соответственно), I_н и U_н− пределы измерения приборов (номинальные значения).

Абсолютные погрешности для сопротивлений (Δ R) взять равными 5% от их номиналов.

Результаты вычислений занесите в соответствующие таблицы.

2. С учетом погрешностей постройте графики зависимостей  при , и  при .

3. Сделайте выводы о видах этих зависимостей и о выполнении закона Ома.

Контрольные вопросы

1. Дайте определения и запишите математические выражения следующих физических величин: сила тока, напряжение, электродвижущая сила, разность потенциалов.

2. Почему единица измерения силы тока имеет эталон и свое определение, а единицы измерения напряжения и сопротивления нет?

3. Поясните причину возникновения электрического сопротивления.

4. Сформулируйте и запишите закон Ома для однородного участка цепи.

5. Какой участок электрической цепи называется однородным?

6. Сформулируйте закон Ома для неоднородного и для замкнутого участков цепи.

7. Изложите идею метода опытной проверки закона Ома для однородного участка цепи. Почему возможны две схемы установки для опытной проверки закона Ома?

Лабораторная работа № 3

Измерение сопротивлений проводникоВмостовыми методами

Цель работы: освоить мостовой метод определения сопротивлений.

Оборудование: лабораторный стенд №3 «Измерение сопротивлений на основе мостовых методов».

Основные теоретические сведения

Электрический ток в металлах представляет собой упорядоченное движение свободных электронов. При этом происходит взаимодействие электронов с ионами кристаллической решетки металла, что является причиной появления сопротивления – противодействия проводника протеканию в нем электрического тока.

Сопротивление проводника зависит от его размеров и природы материала, из которого он изготовлен (строения кристаллической решетки):

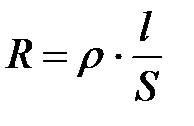                                         (1)

где l – длина проводника,

S – площадь его поперечного сечения,

ρ − удельное сопротивление.

Удельное сопротивление вещества – это сопротивление проводника, длиной 1 м и площадью поперечного сечения 1 м², изготовленного из данного вещества.

Единицей измерения сопротивления проводника в СИ является 1 Ом – сопротивление такого проводника, в котором при напряжении в 1 вольт, приложенном к нему, сила тока равна 1 амперу.

Кроме того, сопротивление проводника и его удельное сопротивление зависят от температуры:

                                      (2)

                                     (2а)

где t – температура проводника,

α – температурный коэффициент сопротивления,

ρ ₀ – удельное сопротивление при t = 0⁰С,

– сопротивление проводника при t = 0⁰С.

При низких температурах данной зависимостью можно пренебречь.

Расчет сопротивления проводников по формуле (1) не всегда возможен, поэтому зачастую для расчета сопротивлений простейших электрических цепей используется следствие из закона Ома в виде:

                                             (3)

где I – сила тока на участке цепи, U – напряжение на этом участке.

Однако на практике более широкое применение имеют сложные цепи, имеющие множественные ветви и узлы. Ветвью называют весь участок цепи между двумя соседними узлами, в котором все элементы соединены последовательно. Узлом электрической цепи называют место соединения трех или большего числа ветвей. Любой замкнутый путь, проходящий по нескольким ветвям, называют контуром электрической цепи. Расчет параметров таких сложных электрических цепей с использованием только закона Ома, не всегда представляется возможным и поэтому в большинстве случаев применяются правила Кирхгофа.

Первое правило Кирхгофа - правило узлов: алгебраическая сумма токов в узловой точке равна нулю, или математически:

                  (4)

противоположно положительной

Рис. 1 Правило узлов

При составлении уравнений, согласно первому правилу Кирхгофа, необходимо произвольно выбрать направления токов во всех ветвях и обозначить их на схеме стрелками. В каждом узле должны быть как входящие, которые принято брать положительными, так и выходящие, считающиеся отрицательными.

Например, для узловой точки, изображенной на рисунке 1: токи I₁, I₂, I₄, будут иметь знак « +», а токам I₃, I₅, - приписываем знак « -».

Тогда, записывая уравнение, получаем:

                                 (5)

Обобщением закона Ома для разветвленных цепей является второе правило Кирхгофа: в любом замкнутом контуре разветвлённой электрической цепи алгебраическая сумма падений напряжений на сопротивлениях в любом контуре равна алгебраической сумме ЭДС, действующих в этом контуре.

Математическая запись второго правила Кирхгофа:

Рис. 2. Применение правил Кирхгофа.

ℰ _i       (6)

Применяя правила Кирхгофа для расчета сложных цепей необходимо выполнить определенные операции:

1. Выбрать (выделить) в цепи независимые замкнутые контуры (содержащие хотя бы 1 элемент цепи, не встречавшийся в ранее выбранных, при этом первый контур всегда независим).

2. Указать на схеме (произвольно) направление токов на отдельных участках выбранных контуров (с учетом особенностей применения первого правила).

3. Выбрать произвольно направление обхода независимых замкнутых контуров (по направлению часовой стрелки или против него), одинаковое для всех.

4. Определить знаки Э. Д. С и токов в выбранных контурах. При этом положительными считаются те токи, направление которых совпадает с направлением обхода, а отрицательными - токи, направление которых противоположно направлению обхода. Знак Э. Д. С принимается положительным, если при обходе контура переход внутри источника осуществляется от минуса к плюсу.

В качестве примера рассмотрим схему, представленную на рисунке 2. Число уравнений, составленных по первому правилу Кирхгофа должно быть на 1 меньше, чем узлов, тогда имея два узла ( A и D ), запишем для узла D уравнение:

Для контура ABCD, второе правило Кирхгофа запишется в виде:

-ℰ ₁,

а для контура ADEF:           ℰ ₂

Решая полученную систему из трех уравнений, используя известные величины, можно рассчитать искомые параметры. Если указано внутреннее сопротивление источников, то его тоже необходимо учитывать при записи уравнений по второму правилу.

Правила Кирхгофа применяются в мостовых методах определения сопротивлений в цепях постоянного тока.

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: