 |
Начисление процентов m раз в году
|
|
|
|
ФИЛИАЛ
федерального государственного образовательного учреждения
высшего профессионального образования
«СЕВЕРО-ЗАПАДНАЯ АКАДЕМИЯ ГОСУДАРСТВЕННОЙ СЛУЖБЫ»
В г. Северодвинске (Архангельская область)
(Филиал СЗАГС в г. Северодвинске (Архангельская область))
Конспект лекций
По дисциплине: «Актуарная и финансовая математика»
Часть II
денежные платежи
для студентов специальности
080105 «Финансы и кредит»
080504 «Государственное и муниципальное управление»
Павлова А.Н.
Северодвинск
Потоки платежей.. 3
Классификация финансовых рент. 4
Годовой аннуитет. 4
Начисление процентов m раз в году. 6
Детерминированная p – срочная рента, m=1. 6
Детерминированная p – срочная рента, m ≠ p. 7
Детерминированная p – срочная рента, m = p. 7
Непрерывное начисление процентов. 7
Вечная рента (бессрочный аннуитет) 8
Отложенная рента. 8
Определение параметров финансовой ренты.. 8
Конверсия финансовых рент. 10
Консолидация платежей.. 10
Список литературы... 12
Потоки платежей
Очень часто в контрактах финансового характера предусматривают не отдельные разовые платежи, а серию платежей, распределённых во времени. Примерами могут быть регулярные выплаты с целью погашения долгосрочного кредита вместе с начисленными на него процентами, периодические взносы на расчетный счет, на котором формируется некоторый фонд различного назначения. (инвестиционный, пенсионный, страховой, резервный, накопительный) дивиденды, выплачиваемые по ценным бумагам, выплаты пенсий из пенсионного фонда и так далее.
Опр. Ряд последовательных поступлений и выплат называют потоками платежей[1](flow of payments).
Опр. Денежный поток или поток наличных денег [cash flow]- это численный ряд, состоящий из последовательности распределённых во времени платежей[2].
|
|
|
Опр. Погашение задолженности в рассрочку, периодическое поступление доходов от инвестиций, выплата пенсий и т.д. - называют потоки платежей.
Отдельный элемент такого ряда может иметь как положительное, так и отрицательное значение.
Численное значение денежного потока характеризует величину притока денег, если оно больше нуля, или оттока денег, если оно меньше нуля. Положительный денежный поток формируют денежные средства, поступившие в экономический субъект по итогам за соответствующий период, например, поступления от продажи товаров, выполнения работ, оказания услуг. Отрицательный денежный поток формируют денежные средства, затрачиваемые экономическим субъектом в соответствующий период, например, инвестиции, возврат кредита, затраты на сырьё, энергию, материалы и др.
Потоки платежей могут быть регулярными и нерегулярными. В нерегулярном потоке платежей членами являются как положительные (поступления), так и отрицательные величины (выплаты), а соответствующие платежи могут производится через разные интервалы времени.
Анализ потока платежей предполагает расчет одной из двух обобщающих характеристик: наращенной суммы или современной стоимости.
Опр. Наращенная сумма – это сумма всех членов потока платежей с начисленными на них к концу срока процентами.
Опр. Современная стоимость потока платежей – это сумма всех его членов, дисконтированных на некоторый момент времени совпадающий с началом потока платежей предшествующий ему.
Опр. Поток платежей, все члены которого - положительные величины, а временные интервалы между последовательными платежами постоянны, называется финансовой рентой или просто рентой (аннуитетом).
Классификация финансовых рент
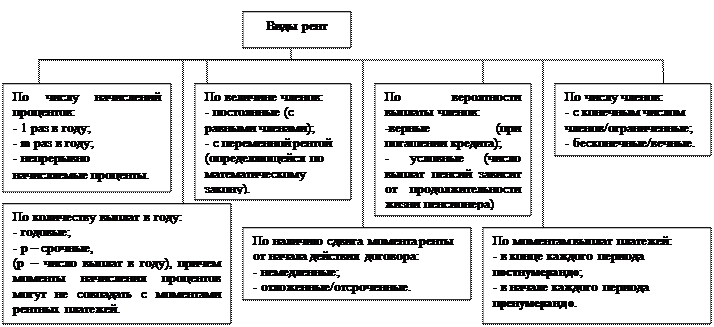
Годовой аннуитет
|
|
|
Рента (аннуитет) характеризуется следующими параметрами:
Член ренты - размер отдельного платежа;
Период ренты - временной интервал между двумя последовательными платежами;
Срок ренты - время от начала первого периода ренты до конца последнего периода;
Процентная ставка – ставка, используемая при наращении или дисконтировании плетежей, образующих ренту.
R - величина годового платежа в аннуитете;
i - процентная ставка сложных процентов, используемая для расчета наращения или дисконтирования платежей;
PVk - современная стоимость k - ого платежа;
PV - современная стоимость всего аннуитета;
FVk - будущая стоимость к - ого платежа;
FV - будущая стоимость всего аннуитета.
Обобщающими показателями аннуитета являются: современная стоимость всего аннуитета (PV) и будущая стоимость всего аннуитета (PV).
Наращенная сумма, то есть сумма всех членов потока платежей с начисленными на них процентами на конец срока определяется по формуле
.
Современная стоимость, то есть сумма современных стоимостей членов потока платежей, определяется по формуле:
.
Рассмотрим аннуитет постнумерандо.
В течении n лет в банк в конце каждого года вносится по R руб.На взносы начисляются сложные проценты по ставке i. Все члены ренты, кроме последнего, приносят проценты. На вносимые платежи один раз в год начисляются проценты по ставке i., тогда первый взнос к концу первого срока ренты возрастет до величины 
, так как на сумму R проценты начислялись за (n-1) год. Если переписать этот ряд в обратном порядке, то получим геометрическую[3]:
,
в которой первый член равен R;
знаменатель (1+i);
число членов n.
Будущая наращенная стоимость аннуитета:
.
Величину 
называют коэффициентом наращения ренты/аннуитета, его обозначение FVIFAi,n [Future Value of Interest Factor of Annuity]. Значения коэффициента наращения табулированы (см. Приложение IV).
Итак, формула наращенной суммы аннуитета постнумерандо:
.
Формула наращенной суммы аннуитета пренумерандо:
Таким образом,
Если платежи вносятся в середине периода, то формула наращенной суммы
.
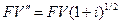Найдем современную стоимость аннуитета постнумерандо:
.
Величина 
называется коэффициентом приведения аннуитета/ренты, его обозначение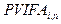 
[Present Value of Interest Factor of Annuity]. Коэффициенты приведения аннуитета табулированы (см. Приложение V). Итак, формула современной стоимости аннуитета постнумерандо:
|
|
|
.
Формула современной стоимости аннуитета пренумерандо
.
Зависимость между наращенной и современной стоимостью аннуитета постнумерандо
.
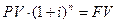Это означает, что если мы внесем в банк разовый платеж величиной PV, то через n лет мы будем иметь наращенную сумму FV, то есть аннуитет можно заменить разовым платежом.
Если платежи вносятся в середине периода, то формула современной стоимости
Задача
Определить современную стоимость и наращенную сумму аннуитета постнумерандо. Срок ренты 5 лет, разовый платеж 4 000 руб. вносится ежегодно. На поступившие взносы начисляются проценты по сложной ставке 8 % годовых.
Решение
Современная стоимость аннуитета равна
PV = 4 000 Ч PVIFA8 %; 5 = 4 000 Ч 3,99271=15 970,84 руб.
Будущая (наращенная) стоимость ренты составит
FV= 4 000 Ч FVIFA 8 %; 5 = 4 000 Ч 5,866601 = 23 466,40 руб.
Ответ: A=15 970,84 руб/, S = 23 466,40 руб.
Начисление процентов m раз в году
Рассмотрим годовую ренту постнумерандо. Проценты начисляются m раз в году. Члены ренты с начисленными к концу срока процентами образуют ряд (перепишем его в обратном порядке):
где j - номинальная ставка процентов.
Мы имеем дело в геометрической последовательностью.
в которой первый член равен R;
знаменатель (1+j/m)m;
число членов n.
Наращенная сумма аннуитета постнумерандо равна:
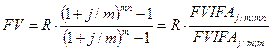[4].
Формула наращенной суммы аннуитета пренумерандо:
.
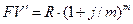Современной стоимости аннуитета постнумерандо:
.
Современной стоимости аннуитета пренумерандо:
Зависимость между наращенной и современной стоимостью аннуитета постнумерандо
.
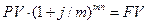Детерминированная p – срочная рента, m=1
Найдём наращенную сумму при условии, что рента выплачивается p раз в году равными платежами.
Если R – годовая сумма, то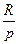 
- размер отдельного платежа.
Мы имеем дело в геометрической последовательностью.
в которой первый член равен ;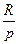
знаменатель (1+i)1/p;
число членов np.
Наращенная сумма рассматриваемой ренты постнумерандо:
.
Наращенной суммы аннуитета пренумерандо:
|
|
|
.
Детерминированная p – срочная рента, m ≠ p
При начислении рентных платежей p раз в году с начислением процентов m раз в году, при условии, что m ≠ p:
Наращенная сумма рассматриваемой ренты постнумерандо:
.
Наращенной суммы аннуитета пренумерандо:
.
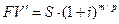Современной стоимости аннуитета постнумерандо:
Детерминированная p – срочная рента, m = p
В контрактах часто начисление процентов и поступление платежа совпадают по времени. Таким образом, число платежей в году p раз ч число начислений процентов m раз в году совпадает.
Наращенная сумма рассматриваемой ренты в конце периода:
.
Наращенная сумма аннуитета в начале периода:
.
Современная стоимость аннуитета постнумерандо:
Современная стоимость аннуитета пренумерандо:
.
|
|
|
