 |
Их связь с бесконечно малыми.
|
|
|
|
Лекция8
Понятие функции одной и нескольких переменных
Если каждой точке 
по некоторому правилу 
ставится в соответствие единственное действительное число 
Ø, то называют функцией, причем называют D – область определения функции; E– область изменения функции.
Точка 
является аргументом функции. Правило , однако, применимо не к самой точке, а к ее координатам.
Таким образом, функция 
устанавливает связь между точками и точками некоторого множества одномерного пространства 
.
Область определения 
четной и нечетной функции симметрична относительно начала координат. Если это условие не выполнено, то функция не является четной и не является нечетной.
1) Функция 
называется периодической, если существует такое положительное число Т, что при любом значении 
выполняется равенство
,
число Т называют периодом функции.
2) Функция называется возрастающей на множестве 
, если большему значению аргумента соответствует большее значение функции, то есть для любых 
, таких, что 
, выполняется неравенство 
.
3) Функция называется убывающей на множестве 
, если большему значению аргумента соответствует меньшее значение функции: если
, то 
для любых .
Основные элементарные функции, их графики
Особую роль в математическом анализе играют элементарные функции.
Основными элементарными функциями называют:
1) степенную функцию 
;
2) логарифмическую функцию 
;
3) показательную функцию 
;
4) тригонометрические функции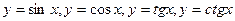 
;
5) обратные тригонометрические функции 
.
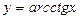Функцию называют элементарной, если ее аналитическое выражение составлено из основных элементарных функций с помощью четырех арифметических действий и операции суперпозиции (функции от функции), примененных конечное число раз.
|
|
|
Предел функции в точке
Говорят, что 
есть предельная точка множества , если в любой окрестности этой точки содержится бесконечное множество точек 
.
Обозначают 
.
Используя логические символы данное определение можно записать таким образом:
, что для 
, как только 
, выполняется 
.
В частности,
1) для функции одной переменной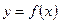 
;
- предельная точка.
Определение предела 
можно записать таким образом:
, что для 
: как только 
выполняется 
;
Односторонние пределы функции одной переменной.
Теорема существования предела
Предел функции 
при 
называется левосторонним и обозначается 
,если точка 
остается все время слева от 
, что означает выполнение неравенства 
.
Аналогично определяется и обозначается правосторонний предел: 
Теорема о существовании предела.
Функция 
имеет в точке предел, равный 
, тогда и только тогда, когда существуют односторонние пределы в точке , и они равны между собой и равны числу .
Бесконечно малые функции, их классификация
Важное значение в дальнейшем имеют функции, пределы которых в точках равны нулю.
· Функция 
называется бесконечно малой в точке , если 
.
· Классификация бесконечно малых функций
Если 
, причем 
и 
то 
и 
называются бесконечно малыми одного порядка малости (скорости приближения и к нулю являются почти равными).
Если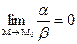 
, то - бесконечно малая более высокого порядка малости, чем ( приближается к нулю быстрее, чем ). Обозначают 
.
Если 
, то и называются эквивалентными бесконечно малыми в окрестности точки М0 ( и приближаются к 0 с одной скоростью). Обозначают: ~ .
Бесконечно большие функции одной переменной,
их связь с бесконечно малыми.
Рассмотрим функцию , определенную на множество , - предельная точка множества .
Функция 
называется бесконечно большой при , если для любого, даже сколь угодно большого положительного числа 
, найдется такое положительное число 
(зависящее от 
, что для всех , не равных и удовлетворяющих условию , будет верно неравенство 
.
|
|
|
Запись того, что функция бесконечно большая при , следующая:
или 
при .
Краткая запись этого определения:
функция бесконечно большая при , если для
, что 
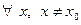; выполняется
Для бесконечно больших функций имеют место следующие свойства.
Если 
и 
, (, ), тогда
1) 
2) 
3) если 
, то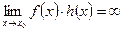 
4) Связь между бесконечно малой 
и бесконечно большой функциями отметим в следующем свойстве:
если функция есть бесконечно малая величина при 
, то функция 
является бесконечно большой при .
И обратно, если функция бесконечно большая при , то функция 
есть величина бесконечно малая при .
То есть, если 
, то 
и наоборот, если 
, то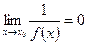 
.
Например, 
является бесконечно малой при 
, тогда 
, то есть является бесконечно большой при .
Теоремы о пределах.
Пусть и 
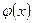- функции, для которых существуют пределы при (или при 
): , 
.
Сформулируем основные теоремы о пределах.
1. Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, то есть
.
2. Предел произведения конечного числа функций равен произведению пределов этих функций, то есть
.
В частности, постоянный множитель можно выносить за знак предела, то есть 
.
3. Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю), то есть
.
4. Если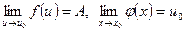 
, то предел сложной функции f[ 
(x)] равен
.
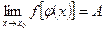5. Теорема о переходе к пределу в неравенстве.
Если в некоторой окрестности точки
, то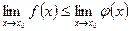 
.
6. Теорема о пределе промежуточной функции.
Если в некоторой окрестности точки функция заключена между двумя функциям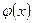и и 
, имеющими одинаковый предел - число ,
то функция имеет тот же предел ,
то есть, если
и 
,
то
Первым замечательным пределом называют 
,
Вторым замечательным пределом называют
или
,
где число e = 2.71828… - иррациональное число, называемое неперовым числом, так как найдено Непером в XVII веке. Число e находит применение в математическом анализе, является основанием натуральных логарифмов.
|
|
|
