 |
Непрерывность функции
|
|
|
|
В точке, на отрезке, в области.
Функция u = f(M) называется непрерывной в точке М0, если она определена в этой точке и ее окрестности и
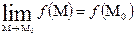 .
.
Функция u = f(M) называется непрерывной в области D, если она непрерывна в каждой точке этой области.
Функция одной переменной y = f(x) называется непрерывной на интервале (a, b) или на отрезке [a, b], если она непрерывна в каждой точке этого интервала или этого отрезка.
Для функция одной переменной y = f(x) определение непрерывности в точке, используя теорему о существовании предела, можно сформулировать таким образом:
функция y = f(x) является непрерывной в точке х = х0 , если:
1) функция определена в этой точке х = х0 и ее окрестности;
2) существуют односторонние пределы:
 ;
;
3) односторонние пределы равны и равны значению функции в точке х0:
 ;
;
Данное определение часто используют на практике при исследовании функции на непрерывность.
Приведем краткую запись определения непрерывности функции в точке х0
 f – непрерывна в т. х0,если
f – непрерывна в т. х0,если 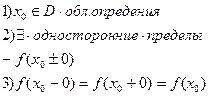
Имеют место следующая
Теорема (об арифметических операциях над непрерывными функциями в точке):
Если функции f1(M), f2(M) непрерывна в точке М0, то будут непрерывными в этой точке также функции:

Из определения непрерывности функции в точке  , следует, что символы предела и функции можно переставить, если функция непрерывна в точке
, следует, что символы предела и функции можно переставить, если функция непрерывна в точке  , то есть
, то есть
 .
.
Точки разрыва функции одной переменной, их классификация
В предыдущем разделе введено понятие функции непрерывной в точке:
Функция y = f(x) является непрерывной в точке х = х0 , если:
1) она определена в этой точке х = х0 и ее окрестности;
2) существуют односторонние пределы:
 ;
;
3) односторонние пределы равны и равны значению функции в точке х0:
|
|
|
 ;
;
Таким образом, для непрерывной функции в точке х  необходимо и достаточно, чтобы
необходимо и достаточно, чтобы

Функция имеет точкуразрыва, если хотя бы одно из условий 1)-3)
не выполнено в точке х 
Введем следующую классификацию точек разрыва:
§ Точка  называется точкой разрыва 1го рода, если существует
называется точкой разрыва 1го рода, если существует
-односторонние пределы, они конечны, но не равны друг другу
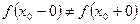 (разрыв конечного скачка);
(разрыв конечного скачка);
-односторонние пределы равны, но не равны значения функции в точке 
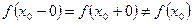 (устранимый разрыв).
(устранимый разрыв).
Лекция 9
Свойства функций, непрерывных на отрезке
Теорема 1 (об ограниченности непрерывной функции)
Если функция  непрерывна на отрезке
непрерывна на отрезке 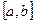 , то она ограничена на этом отрезке: k≤ f(x)≤K
, то она ограничена на этом отрезке: k≤ f(x)≤K
Теорема 2 (теорема Вейерштрасса).
Если функция  непрерывна на отрезке
непрерывна на отрезке 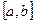 , то она достигает на этом отрезке наименьшего значения
, то она достигает на этом отрезке наименьшего значения  и наибольшего значения
и наибольшего значения 
Теорема 3 (теорема Больцано-Коши).
Если функция непрерывна на отрезке 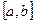 и значения ее на концах отрезка
и значения ее на концах отрезка  и
и  имеют противоположные знаки, то есть f(a) f(b) < 0,
имеют противоположные знаки, то есть f(a) f(b) < 0,
то внутри отрезка найдется точка 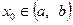 такая, что
такая, что  .
.
Теорема 4 (о непрерывности основных элементарных функций).
Основные элементарные функции непрерывны в области определения.
Аналогичная теорема имеет место для элементарных функций, то есть функций, полученных из основных элементарных с помощью операций сложения, вычитания, умножения, деления и суперпозиции (функция от функции).
Теорема 5 (о непрерывности элементарных функций).
Элементарные функции непрерывны в области определения
Теорема 6 (о промежуточных значениях непрерывной функции).
Пусть функция непрерывна на некотором отрезке (в том числе бесконечном). Если в двух каких- либо точках этого отрезка а и в функция принимает различные значения: f(a)=A; f(b)=B, то каково бы ни было С, лежащее между А и В, найдется x 
 , лежащее между а и b, что f(x
, лежащее между а и b, что f(x  )= C.
)= C.
Непрерывная функция, переходя от одного значения к другому, принимает хотя бы раз и всякое промежуточное значение.
|
|
|
|
|
|


