 |
Обработка сигналов измерительной информации. Вычисление результатов косвенных, совокупных и совместных измерений.
|
|
|
|
Преобразование сигналов измерительной информации. Линеаризация характеристик преобразования разбиением на участки.
В общем случае кривая X= f(UX) может быть разбита на конечное число i участков (рисунок 2.10), каждый из которых может быть аппроксимирован двучленом первой степени
X = a i + b iUX. (2.37)
При разбиении кривой на четыре участка, как показано на рисунке 2.11, справедливы соотношения
X = а 3 + b 3UX для UX3 < UX,
X = а 2 + b 2UX для UX2 < UX < UX3,
X = a 1 + b 1UX для UX1 < UX < UX2,
X = а 0 + b 0UX для UX < UX1.
Каждый раз, когда текущее значение UXпереходит границу того или иного участка, значение напряжения Uвых = AХизменяется соответственно наклону данного участка кривой. Это осуществляется с помощью сумматоров, пороги которых соответствуют различным границам UXi, и каждый из которых выдает напряжение Ui, равное нулю или пропорциональное UXi – UX в зависимости от того, превосходит или нет значение UXпорог сумматора.
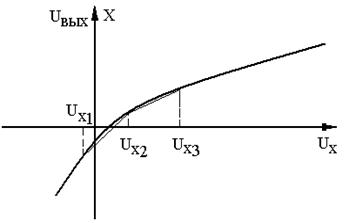
Рисунок 2.10 – Кусочно-линейная аппроксимация нелинейной функции.
Диаграмма аппроксимации кривой
На рисунке 2.11представлено аппроксимирующее устройство, позволяющее осуществить линеаризацию функции, разбитой на четыре участка (см. рисунок 2.10). Выходное напряжение устройства имеет форму
Uвых = Ai + BiUX. для UXi < UX < UXi+1, (2.38)
где Ai - A a i и Bi = A b i.
Если границы участков задать в соответствии со значениями
 ,
,  ,
,  , (2.39)
, (2.39)
то напряжение UВЫХ на выходе устройства будет равно
 . (2.40)
. (2.40)
Значения U в различных случаях составят:
при UX > UX3 U3 = U2 = U1 = 0;
при UX2 < UX < UX3 U3 = UX3 - UX, U2 = U1 = 0;
при UX1 < UX < UX2 U3 = UX3 - UX, U2 = UX2 – UX, U1 = 0;
при UX < UX1 U3 = UX2 - UX, U2 = UX2 - UX, U1 = UX1 - UX.

Рисунок 2.11 - Кусочно-линейная аппроксимация нелинейной функции. Принципиальная схема аппроксиматора сигнала
|
|
|
Требуемые номиналы элементов схемы определяются из следующих соотношении:
 .
.
Преобразование сигналов измерительной информации. Цифровые методы линеаризации.
Их использование, очевидно, требует, чтобы измеряемое напряжение UХ было предварительно преобразовано в цифровую форму.
Цифровая система обработки данных (например, ЭВМ) позволяет осуществить линеаризацию функции преобразования по программе с приемлемой скоростью. Характеристику Ul = f(UХ) разбивают на определенное число участков (рисунок 2.12), и абсциссы их границ записывают в память ЭВМ.
Измеряемое напряжение UXсравнивается с этим набором абсцисс: UХi, UХ, UХi+1. Когда таким образом определяется номер i участка, запускается программа для расчета Uвых по алгоритму линейно-кусочной аппроксимации:

Рисунок 2.12 - Кусочно-линейная аппроксимация функции
при использованию цифрового метода обработки данных
 . (2.41)
. (2.41)
Постоянные коэффициенты, определяющие наклон прямых каждого из участков, должны также храниться в памяти. При такой последовательной обработке данных необходимо учитывать время проведения операций, позволяющее получать результаты с требуемой скоростью.
Обработка сигналов измерительной информации. Вычисление результатов косвенных, совокупных и совместных измерений.
Эта задача возникает в тех случаях, когда некоторые физические величины не удается измерить прямым методом с помощью измерительных Преобразователей или приборов, непосредственно реагирующих на эти величины, но можно измерить прямым методом некоторые другие физические величины, связанные с ними известными однозначными функциональными зависимостями. Если искомая величина выражена в явном виде в функции величин у1, у2,..., yn измеряемых прямым методом, то измерение их в сочетании с вычислением функции
Х = F(Y1,Y2,...,Yn) (2.43)
называется косвенным измерением.
|
|
|
Если требуется найти значения нескольких величин X1, Х2,..., Хm, которые входят в систему уравнений вида
 (2.44)
(2.44)
то измерение величин Y1, Y2,..., Yn в сочетании с решением системы уравнений называют совокупным или совместным измерением.
Первый термин относится к случаю, когда Х1, Х2,..., Хm - одноименные величины, второй - когда эти величины разноименны.
Примером косвенного измерения может служить определение сопротивления резистора с помощью амперметра и вольтметра по формуле
 . (2.45)
. (2.45)
Примером совместных измерений является определение электрического сопротивления при 20 °С (R20) и температурного коэффициента терморезистора по данным прямых измерений его сопротивления при температурах q1и q2, отличных от 20 °С. Для этого необходимо решить систему уравнений
 (2.46)
(2.46)
Решение подобных задач может потребовать выполнения громоздких вычислений, которые под силу лишь сложному устройству обработки информации или универсальной ЭВМ.
|
|
|


