Обработка сигналов измерительной информации. Сглаживание данных.

На выходной сигнал преобразователя u(t), соответствующий функции Х(t), может быть наложена помеха в виде случайной функции времени S(t). Действие ее можно исключить или ослабить сглаживанием суммарного сигнала, поступающего на вход измерительной системы. Сглаживание следует выполнять так, чтобы результат достаточно точно повторял функцию X(t). Если частотные спектры перекрываются частично, то такой фильтр ослабляет часть помехи. Физическая реализация схемы фильтра с применением реактивных элементов - конденсаторов, дросселей, трансформаторов - может оказаться затруднительной, особенно когда требуется получить сравнительно малое значение верхней граничной частоты, например сотые доли герца.

Действие фильтра может быть заменено определенной математической обработкой функции времени, выражаемой входным суммарным сигналом:

u_S(t) = u(t) + s(t). (2.47)

Один из видов такой обработки - это вычисление текущего среднего значения по формуле

. (2.48)

При этом обязательно выполнение следующего условия: период верхней частотной составляющей спектра сигнала u(t) должен в несколько раз превышать период исследуемого сигнала. Если одновременно оказывается, что период нижней частотной составляющей спектра помехи S(t) в несколько раз меньше периода полезного сигнала, то результат интегрирования достаточно точно повторяет форму сигнала u(t). Если соблюдается первое условие, а второе не соблюдается, то помеха подавляется частично.

Интегрирование по (2.48) означает, что в момент t вместо ординаты u_S(t) выдается среднее значение u_S, найденное по интервалу шириной T, от t - Т до t, г.е. площадь заштрихованного участка на рисунке 2.14, а, деленная на T. С течением времени t интервал усреднения непрерывно скользит вправо, сохраняя ту же ширину Т (см. пунктирные границы на той же диаграмме для нового момента времени t₁).

При вычислении интеграла (2.48) на ЭВМ непрерывная функция u_S(t) заменяется последовательностью дискретных ординат, взятых через интервал q (рисунок 2.14, б). Обозначим u_i ординату, соответствующую текущему значению времени t. Тогда ближайшая предшествующая ордината обозначается U_i-1, ей предшествует и_i-2 и т.д. Предположим, в интервал Т умещается n интервалов q. Тогда интеграл (2.48) заменяется суммой

. (2.49)

Со сдвигом на очередной шаг q в сумму вовлекается следующая ордината функции u_S(t), но исключается ордината, которая в (5.54) обозначена u_i-n.

Для выполнения этих действий ЭВМ должна содержать в своей оперативной памяти наряду с очередным результатом усреднения U_i^* еще и значения n+1 ординат. При большом числе обрабатываемых величин становится важной задача экономного использования памяти ЭВМ.

Рисунок 2.14 – Сглаживание данных

Известен и широко применяется другой вариант сглаживания, требующий меньшего объема памяти. Сущность его заключается в том, что при получении очередной ординаты сглаживаемой функции u_i выполняется операция

, (2.50)

где u_i^* - результат сглаживания на очередном шаге;

u^*_i-1 - результат сглаживания на предыдущем шаге;

q - коэффициент, меньший 1.

Это означает усреднение, при котором вес каждой ординаты функции U_S(t) уменьшается по мере ее удаления в прошлое от текущего момента t. При этом быстрота уменьшения веса прошлых ординат задается значением q. Рекуррентное соотношение (2.50) преобразуется в выражение

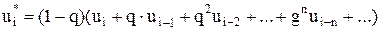. (2.51)

Легко убедиться, что если u_S в течение длительного времени равно постоянной величине U₀, то

(2.52)

Выражение в скобках справа представляет собой сумму членов убывающей геометрической прогрессии, стремящуюся при возрастании числа членов к значению 1/(1-q). Следовательно, результат сглаживания в этом случае будет стремиться к u(t). Если максимальная скорость изменения u(t) такова, что изменение и за несколько шагов q не превышает допустимой погрешности измерения, то рассматриваемое сглаживание не исказит существенно функцию u(t), В то же время более быстрые помехи S(t), входящие в состав суммарного сигнала u_S(t), будут в значительной мере сглажены, поскольку от каждого приращения и_S за один шаг q в выходной сигнал и_i^* входит относительно малая часть, определяемая коэффициентом 1 - q.

Для закона убывания коэффициентов q, q², q³... при членах ряда (2.52) всегда можно подобрать экспоненциальную функцию e^-at из условия, что за время, равное шагу дискретизации q, она должна уменьшиться до значения q:

е^{- а q} = q.

Отсюда

Благодаря убыванию значений коэффициентов ряда по экспоненциальному закону рассматриваемому методу обработки информации присвоено название экспоненциального сглаживания. Он экономичен в отношении требуемого объема оперативной памяти ЭВМ: в ней нужно хранить только последнее значение результата сглаживания.