 |
Определение числа проверочных разрядов
|
|
|
|
Содержание
1. Задание…………………………………………………………………….…3
2. Введение………………………………………………………………….…..3
3. Расчетная часть……………………………………………………………....8
3.1 Определение числа проверочных разрядов……………...............8
3.2 Нахождение проверочного многочлена……………….................8
4. Принцип действия кодирующего устройства……………………….........10
5.. Разработка принципиальной схемы………………………………...…….12
5.1 Используемые микросхемы………………………………...……..12
Список литературы…………………………………………………………....16
ПРИЛОЖЕНИЕ А. Кодирующее устройство
Схема электрическая принципиальная.
ПРИЛОЖЕНИЕ Б. Кодирующее устройство
Перечень элементов.
 1. Задание
1. Задание
Разработка десятиразрядного кодирующего устройства циклического кода по методу проверочного многочлена.
Введение
Помехоустойчивое кодирование нужно для того, чтобы имелась возможность обнаруживать или исправлять ошибки, возникающие при передаче сигнала по каналу связи.
Помехоустойчивое кодирование состоит в целенаправленном введении избыточности для того, чтобы появилась возможность обнаруживать и/или исправлять ошибки, возникающие при передаче по каналу связи. Введение избыточности означает, что, кроме информационной последовательности (которая отвечает за передачу полезного сигнала), в передаваемое сообщение вводят проверочные символы, которые вместе с информационными участвуют
в процессе обнаружения и исправления ошибок.
Избыточные коды делятся на блоковые и непрерывные. В блоковых кодах информационная последовательность разбивается на отдельные блоки– информационные и проверочные. Общее число элементов кодовой комбинации в этом случае n=k+r, где k – число информационных элементов, r - число проверочных элементов. При этом кодовая комбинация передаётся целиком, а её обработка производится по отдельности для информационных и проверочных частей. В непрерывных кодах передаваемая информационная последовательность не разделяется на блоки, а проверочные элементы размещаются в определённом порядке между информационными. Процессы кодирования и декодирования здесь также имеют непрерывный характер.
|
|
|
По своим декодирующим свойствам избыточные коды делятся на обнаруживающие и исправляющие ошибки. Корректирующие свойства определяются величиной избыточности кода, т.е. чем выше избыточность кода, тем лучше его корректирующие свойства.
Степень отличия любых двух кодовых комбинаций характеризуется расстоянием между ними в смысле Хэмминга – кодовым расстоянием. Оно выражается числом символов, в которых комбинации отличаются одна от другой, и обозначается d.
Корректирующие свойства кода определяются минимальным кодовым расстоянием d0 – расстоянием Хемминга между двумя разрешёнными кодовыми комбинациями. Для исправления одиночных ошибок расстояние Хэмминга должно быть не меньше 3.
Линейными или систематическими (n, k)-кодами называются коды, у которых проверочные элементы являются линейными комбинациями информационных. При двоичном кодировании такой линейной операцией является операция сложения «по модулю 2».
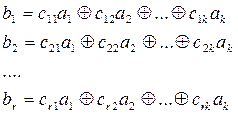 (1)
(1)
где а1,…., ак – информационные разряды; b1,…br – проверочные разряды; коэффициенты cij принимают значения 0 или 1 в зависимости от выбранных групп информационных элементов, участвующих в формировании проверочных.
Количество r проверочных элементов определяется исходя из обеспечения заданного расстояния Хемминга d0. В общем случае эта задача не имеет однозначного решения. Для случая одиночной  исправляемой ошибки (или однократной) формула оценки r имеет вид:
исправляемой ошибки (или однократной) формула оценки r имеет вид:
|
|
|
 (2)
(2)
Циклические коды характеризуются более формализованным выбором проверочных элементов. Широкое распространение циклических кодов обусловлено также их высокой способностью обнаруживать и исправлять ошибки различной конфигурации, простой технической реализацией, удобством математического аппарата, их анализа и синтеза.
В основе построения циклических кодов лежит представление кодовых комбинаций в виде многочленов, а также алгебры данных многочленов, определяющей умножение, деление и сложение этих многочленов. Кодовые слова двоичного линейного кода можно представить в виде многочлена:

 (3)
(3)
где коэффициенты аi равны 0 или 1 и соответствуют разрядам двоичного числа.
Циклические коды относятся к блоковым кодам, т.е. первые k элементов комбинации циклического кода являются информационными, а последующие r – проверочными. Следовательно, можно ввести в рассмотрение многочлен f(x) степени k-1, отображающий k-элементную комбинацию первичного кода, и многочлен r(x) степени r-1, отображающий комбинацию проверочных элементов. Тогда многочлен комбинации циклического кода:
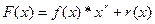 (4)
(4)
Умножение на xr необходимо, чтобы сдвинуть информационные элементы на r разрядов влево и тем самым высвободить справа r разрядов для записи проверочных элементов.
Основная идея циклического кодирования (построение циклических кодов) заключается в том, что многочлен разрешенной  комбинации должен делиться на так называемый образующий многочлен степени r − G(x), т.е.
комбинации должен делиться на так называемый образующий многочлен степени r − G(x), т.е.
 (5)
(5)
где Q(x) – некоторый многочлен, получившийся в результате деления.
Если в результате деления образуется остаток S(x), то этот остаток называется синдромным полиномом (многочленом). Если синдромный полином равен нулю (т.е. деление произошло без остатка), то принятая комбинация является кодовым словом.
Для исправления ошибок необходимо, чтобы остатки от деления (или
синдромные полиномы) служили опознавателями ошибок. При этом каждому варианту ошибок должен соответствовать свой остаток, не совпадающий ни с каким другим, чтобы было возможно однозначно определить места в кодовых комбинациях, где произошли ошибки. Для этого необходимо выбрать образующий многочлен. При выборе должны руководствоваться следующими свойствами образующих многочлены:
|
|
|
1. Образующий полином должен быть неприводимым многочленом, т.е. его нельзя представить в виде произведения многочленов низших степеней.
2. Второе свойство образующего многочлена основано на свойстве
циклических кодов, заключающаяся в том, что циклическая перестановка кодовой комбинации дает разрешенную комбинацию циклического кода. Пусть комбинация  является разрешенной, которой соответствует многочлен
является разрешенной, которой соответствует многочлен

После циклического сдвига имеем следующую разрешенную комбинацию  , которой соответствует многочлен
, которой соответствует многочлен

 (6)
(6)
Так как F1(x) делится на G(x) без остатка, то и для деления F2(x) без остатка на G(x) необходимо, чтобы двучлен (xn+1) делился без остатка на G(x), т.е.
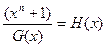 (7)
(7)
где H(x)-проверочный многочлен (используется в декодере). Таким образом, согласно (5), образующий многочлен необходимо выбрать из числа неприводимых, входящих в разложение многочлена xn+1.
Способ формирования комбинаций циклического кода, основанный на свойстве проверочного многочлена H(x). Из формулы (7)
где двучлен xn+1 делится без остатка на G(x) следует, что проверочный многочлен H(x) также может быть использован для задания циклического кода, если проверочный многочлен H(x) представить в виде.

Структурная схема кодера на проверочном многочлене имеет вид: 
 |
Рисунок 1- Структурная схема кодера
Число ячеек (разрядов) регистра для данного случая равно числу информационных элементов.
Рассмотрим принцип работы полученной системы. В исходном состоянии обратная связь разомкнута, ключ в положении 1 и в регистр вводится информационная последовательность f(x), начиная со старшего разряда. Через k-тактов после ввода информационных  символов ключ переводится в положение 2, после чего в течении последующих k-тактов на выход подается информационная последовательность, а в регистре формируются проверочные элементы (символы). После этого ключ переводится в положение 1 и проверочные элементы выдаются на выход кодирующего устройства в течение последующих r тактов.
символов ключ переводится в положение 2, после чего в течении последующих k-тактов на выход подается информационная последовательность, а в регистре формируются проверочные элементы (символы). После этого ключ переводится в положение 1 и проверочные элементы выдаются на выход кодирующего устройства в течение последующих r тактов.
|
|
|
 3. Расчетная часть
3. Расчетная часть
Определение числа проверочных разрядов
Для задания кода по методу проверочного многочлена необходимо выполнение условия (2). Для k=10 получим:
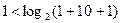 условие не выполняется
условие не выполняется
 условие не выполняется
условие не выполняется
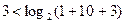 условие не выполняется
условие не выполняется
 условие выполняется
условие выполняется
Таким образом, требуется построить код (14,10).
|
|
|


