|
8.2. Асинхронный ход возбужденного генератора
|
|
|
|
В доаварийном режиме генератор работает синхронно на энергосистему. (рис. 8. 2. )
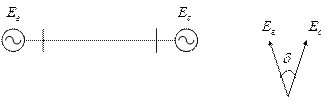
Рис. 8. 2. Схема работы генератора на энергосистему.
При синусоидальных э. д. с. генератора
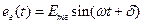 (8. 1)
(8. 1)
и энергосистемы
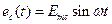 (8. 2)
(8. 2)
и одинаковой частоте вращения  э. д. с. изображаются векторами
э. д. с. изображаются векторами  и
и  , сдвинутыми между собой на угол
, сдвинутыми между собой на угол  . Расчет токов и напряжений в этой схеме выполняется с использованием комплексных величин.
. Расчет токов и напряжений в этой схеме выполняется с использованием комплексных величин.
При асинхронном ходе э. д. с. генератора равна  и э. д. с. энергосистемы
и э. д. с. энергосистемы  , т. е. э. д. с. этих источников имеют разные частоты
, т. е. э. д. с. этих источников имеют разные частоты 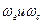 . Положим
. Положим 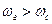 . В таком случае угол будет расти
. В таком случае угол будет расти 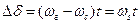 . Здесь время отсчитывается с момента возникновения асинхронного хода;
. Здесь время отсчитывается с момента возникновения асинхронного хода;  - скольжение. Скольжение выражают также в относительных единицах
- скольжение. Скольжение выражают также в относительных единицах  .
.
При возникновении скольжения создается асинхронный момент Мас и генератор генерирует асинхронную мощность. С некоторыми упрощениями можно представить полный электромагнитный момент синхронной машины двумя составляющими: синхронной Мсн и асинхронной Мас, причем М=Мсн+Мас, Соответственно мощность Р=Рсн+Рас. При этом приближенно можно считать, что наличие возбуждения не оказывает влияние на асинхронную составляющую Рас, т. е. при расчетах можно использовать наложение синхронных и асинхронных моментов и мощностей [7].
Синхронная составляющая момента Мсн зависит от параметров машины, тока возбуждения, приложенного напряжения и угла  , а асинхронная составляющая момента Мас - от параметров машины, приложенного напряжения, угла
, а асинхронная составляющая момента Мас - от параметров машины, приложенного напряжения, угла  и скорости его изменения, т. е. скольжения
и скорости его изменения, т. е. скольжения 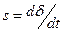 . В упрощенных расчетах оперируют усредненным асинхронным моментом Мас. ср, который не зависит от угла
. В упрощенных расчетах оперируют усредненным асинхронным моментом Мас. ср, который не зависит от угла  .
.
Рассмотрим режим с бесконечно малым скольжением 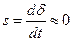 . В таком случае асинхронный момент мал, и его можно не учитывать. Выдаваемая мощность генератора будет определяться только его синхронной мощностью.
. В таком случае асинхронный момент мал, и его можно не учитывать. Выдаваемая мощность генератора будет определяться только его синхронной мощностью.
|
|
|
С учетом сказанного, можно построить векторную диаграмму по рис. 8. 2 для любых значений 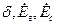 и найти
и найти 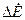 , ток и напряжение в любой точке схемы.
, ток и напряжение в любой точке схемы.
Бесконечно малое скольжение предполагает близость частот  и
и 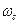 , т. е. наличие в схеме как бы одночастотной э. д. с. Это упрощение помогает раскрыть картину асинхронного режима, выяснить основные закономерности и получить приближенную количественную оценку параметров. Такой подход будет использован нами в начале рассмотрения проблемы. В дальнейшем изложении при построении векторных диаграмм сопротивление Zр в комплексной плоскости будет учтено действие асинхронного момента (мощности), используя при этом принцип суперпозиции, о чем сказано выше.
, т. е. наличие в схеме как бы одночастотной э. д. с. Это упрощение помогает раскрыть картину асинхронного режима, выяснить основные закономерности и получить приближенную количественную оценку параметров. Такой подход будет использован нами в начале рассмотрения проблемы. В дальнейшем изложении при построении векторных диаграмм сопротивление Zр в комплексной плоскости будет учтено действие асинхронного момента (мощности), используя при этом принцип суперпозиции, о чем сказано выше.
Допустимость сделанных упрощений поясним еще раз следующими соображениями. Пусть  и
и  . Уравнительный ток в линии определится разностью э. д. с. источников
. Уравнительный ток в линии определится разностью э. д. с. источников
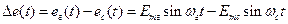 (8. 3)
(8. 3)
Ради упрощения, рассмотрим случай, когда 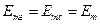 . При этом
. При этом 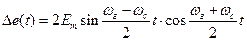 (8. 4)
(8. 4)
или
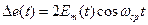 .
.
Из этих формул следует, что 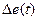 представляет собой гармоническое колебание со средней частотой
представляет собой гармоническое колебание со средней частотой 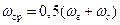 , амплитуда которого изменяется во времени по закону
, амплитуда которого изменяется во времени по закону  . Строго говоря, этот сигнал не является чисто гармоническим, что затрудняет математические операции с ним.
. Строго говоря, этот сигнал не является чисто гармоническим, что затрудняет математические операции с ним.
В инженерных задачах идут на некоторые упрощения, допустимые с точки зрения точности расчетов. Так, при исследовании поведения релейной защиты в асинхронном режиме, следует помнить, что подавляющее большинство реле реагирует на действующее значение тока (напряжения), при этом время наблюдения за сигналом составляет один или почти один период промышленной частоты [17]. В таком случае при частоте скольжения 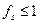 Гц на отрезке времени
Гц на отрезке времени 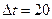 мс можно считать Em(t) = const и рассматривать
мс можно считать Em(t) = const и рассматривать 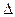 e(t) как гармонический сигнал со средней частотой
e(t) как гармонический сигнал со средней частотой  и постоянной амплитудой.
и постоянной амплитудой.
|
|
|
Для одночастотного сигнала можно оперировать комплексными сопротивлениями
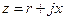 , где
, где  , а также комплексными токами
, а также комплексными токами 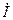 и напряжениями
и напряжениями  .
.
С учетом сказанного, для действующего значения уравнительного тока в линии запишем
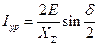 (8. 6)
(8. 6)
График изменения тока в функции угла  показан на рис. 8. 3. На этом же рисунке показано изменение активной мощности генератора, рассчитанной по формуле:
показан на рис. 8. 3. На этом же рисунке показано изменение активной мощности генератора, рассчитанной по формуле:
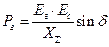 . (8. 7)
. (8. 7)

Рис. 8. 3. График изменения тока  и активной мощности Р(
и активной мощности Р(  ) генератора
) генератора
Из графика следует, что асинхронный режим генератора является очень тяжелым режимом - через генератор протекает очень большой уравнительный ток, а активная мощность принимает весьма большие значения при углах 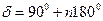 , где п = 0, 1, 2... и меняет свой знак в течение одного проворота ротора.
, где п = 0, 1, 2... и меняет свой знак в течение одного проворота ротора.
Принимая во внимание высказанную выше оговорку об одночастотности сигнала, можно рассчитывать напряжение в n-ой точке сети по формуле:
 .
.
Характерным режимом является случай 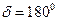 , для которого построена векторная диаграмма на рис. 8. 4. Здесь схема представлена сопротивлениями генератора Zг, линии Zл, и энергосистемы Zc. Э. д. с. генератора Ег и системы Ес приложены по концам схемы и сдвинуты на 180°, что соответствует рассматриваемому случаю.
, для которого построена векторная диаграмма на рис. 8. 4. Здесь схема представлена сопротивлениями генератора Zг, линии Zл, и энергосистемы Zc. Э. д. с. генератора Ег и системы Ес приложены по концам схемы и сдвинуты на 180°, что соответствует рассматриваемому случаю.

Рис. 8. 4. Векторная диаграмма э. д. с. для угла 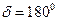
Полагая 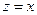 , получим уравнительный ток чисто реактивным, сдвинутым относительно э. д. с. на угол 90°, тогда падение напряжения
, получим уравнительный ток чисто реактивным, сдвинутым относительно э. д. с. на угол 90°, тогда падение напряжения 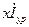 будет совпадать по фазе с направлением э. д. с. В таком случае величина напряжения в точке «n» будет равна
будет совпадать по фазе с направлением э. д. с. В таком случае величина напряжения в точке «n» будет равна  и эпюра напряжений вдоль линии электропередач изобразится прямой, соединяющей концы векторов
и эпюра напряжений вдоль линии электропередач изобразится прямой, соединяющей концы векторов  и
и 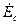 .
.
В некоторой точке Ц, называемой электрическим центром, напряжение равно нулю. Во всех точках сети от э. д. с. Ег до электрического центра напряжение совпадает по направлению с вектором  . После точки Ц напряжение (в точке «т») будет ориентировано согласно с вектором
. После точки Ц напряжение (в точке «т») будет ориентировано согласно с вектором 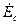 .
.
Для энергосистемы большой мощности можно положить сопротивление энергосистемы  . Тогда вектор Ёс переместится в точку «m» и будет изображаться вектором
. Тогда вектор Ёс переместится в точку «m» и будет изображаться вектором  , а эпюра напряжений вдоль схемы будет определяться линией, соединяющей концы векторов
, а эпюра напряжений вдоль схемы будет определяться линией, соединяющей концы векторов  и
и  . Отсюда следует, что электрический центр также сместится и займет положение Ц*. При работе блока генератор-трансформатор на шины бесконечной мощности электрический центр будет располагаться «внутри» блока генератор-трансформатор.
. Отсюда следует, что электрический центр также сместится и займет положение Ц*. При работе блока генератор-трансформатор на шины бесконечной мощности электрический центр будет располагаться «внутри» блока генератор-трансформатор.
|
|
|
Если э. д. с. генератора уменьшить до значения 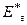 , то эпюра напряжений также изменится. Если генератор невозбужден, т. е.
, то эпюра напряжений также изменится. Если генератор невозбужден, т. е. 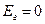 , то центр проворота переместится в нейтраль генератора.
, то центр проворота переместится в нейтраль генератора.
Релейная защита, реагирующая на напряжение (реле напряжения, дистанционное реле) и расположенная вблизи от электрического центра отреагирует на факт снижения напряжения как на короткое замыкание в точке Ц. Это обстоятельство должно учитываться при выборе уставок таких защит.
На рис. 8. 5 показана схема сети и векторная диаграмма напряжения в месте установки реле при асинхронном ходе. Пусть 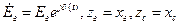 , а также
, а также 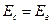 . С изменением угла
. С изменением угла  в схеме действует э. д. с.
в схеме действует э. д. с.
 .
.

Рис. 8. 5. Схема сети (а) и векторная диаграмма (б).
Напряжение  определяется так
определяется так
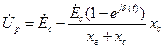 . (8. 9)
. (8. 9)
Обозначим 
 , тогда
, тогда
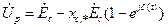 . (8. 10)
. (8. 10)
Это уравнение определяет собой окружность, которая проходит через точки: при  ,
, 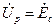 , если
, если 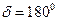 , то
, то 
Для случая  окружность
окружность 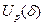 отмечена цифрой 1. При этом конец вектора
отмечена цифрой 1. При этом конец вектора  скользит по окружности 1.
скользит по окружности 1.
Если  , то окружность Up(
, то окружность Up(  ) охватывает начало координат (отмечено цифрой 2). Теперь вектор
) охватывает начало координат (отмечено цифрой 2). Теперь вектор  вращается с частотой
вращается с частотой  и дополнительно колеблется относительно вектора Ег.
и дополнительно колеблется относительно вектора Ег.
Еще раз обратимся к выражению
 . (8. 11)
. (8. 11)
Такая запись формулы справедлива в пределах изменения угла  . При дальнейшем увеличении угла функция
. При дальнейшем увеличении угла функция 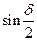 меняет знак, вследствие чего может создаваться неправильное представление, что после
меняет знак, вследствие чего может создаваться неправильное представление, что после  сигнал
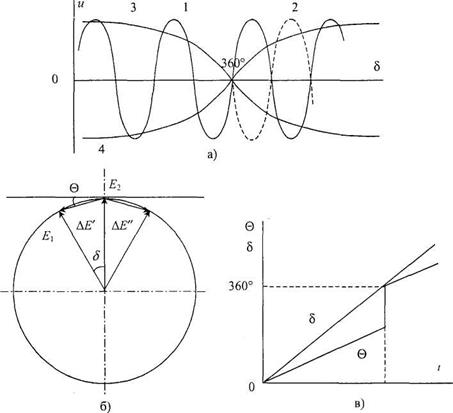
сигнал  следует изображать в виде пунктирной линии 2 (рис. 8. 6), промодулированный по закону
следует изображать в виде пунктирной линии 2 (рис. 8. 6), промодулированный по закону 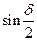 .
.
Для сигнала 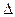 e(t) корректнее оперировать углом
e(t) корректнее оперировать углом 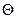 (рис. 8. 6, б). График изменения углов
(рис. 8. 6, б). График изменения углов  и
и 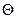 показаны на рис. 8. 6, в. В пределах углов 0-360° формула
показаны на рис. 8. 6, в. В пределах углов 0-360° формула  справедлива, но при дальнейшем скольжении вектора
справедлива, но при дальнейшем скольжении вектора 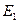 относительно вектора Е2 вектор
относительно вектора Е2 вектор 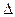 Е" уменьшается до нуля и после угла 360° возрождается в виде
Е" уменьшается до нуля и после угла 360° возрождается в виде 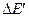 , т. е. как бы поворачивается на 180°. На рис. 8. 6, в это отмечено скачкообразным изменением угла
, т. е. как бы поворачивается на 180°. На рис. 8. 6, в это отмечено скачкообразным изменением угла 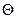 от 180° до 360°. После угла 360° функция
от 180° до 360°. После угла 360° функция 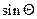 положительна.
положительна.
|
|
|
|
|
Рис. 8. 6. Изменение тока (а) и диаграммы напряжений и э. д. с. (б, в) при асинхронном ходе
|
|
|