 |
8.6. Изменение сопротивления на выводах генератора при асинхронном ходе
|
|
|
|
Рассмотрим схему на рис. 8. 14. Генератор Г работает на энергосистему С. На выводах генератора установлено реле сопротивления, включенное на фазный ток и напряжение.
Примем также, что скольжение 
, т. е изменение угла 
происходит очень медленно. В таком случае асинхронный момент мал, им можно пренебречь и учитывать только синхронный момент (мощность). При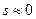 
генератор следует представлять синхронным сопротивлением 
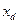. В аналитических выкладках примем пока сопротивление генератора 
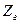и энергосистемы Zc.
При асинхронном ходе частоты 
и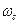 
неодинаковы. Однако с учетом, 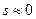можно считать = 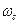и оперировать с одночастотным сигналом со средневзвешенной частотой 
Такое упрощение вполне допустимо и будет использовано для получения зависимости Zp (Ег, Ес, ).
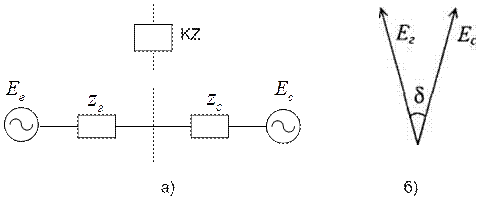
Рис. 8. 14. Схема энергосистемы (а) и диаграмма (б) для определения zp.
Когда скольжение 
, то появится значительный асинхронный момент генератора. В таком случае генератор должен быть представлен сопротивлением, зависящим от скольжения 
(s). Это обстоятельство будет учтено в дальнейшем при анализе этого случая.
Для одночастотного сигнала ток в линии
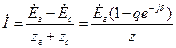, (8. 12)
где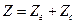 
и q = Ес/Ег.
Напряжение в месте установки реле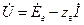 
. Полное сопротивление, измеряемое реле, составляет
. (8. 13)
Учитывая формулу для тока (8. 12), выражение для измеряемого сопротивления приведем к виду
(8. 14)
Если генератор не возбужден, то, как следует из формулы (8. 14), реле сопротивления измерит 
. При Ес = 0 имеем Zp = Zc. Таким образом, в данных режимах реле измерит либо сопротивление генератора, либо сопротивление системы. В других режимах это будет фиктивное сопротивление, обусловленное значениями токов и напряжений
|
|
|
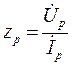
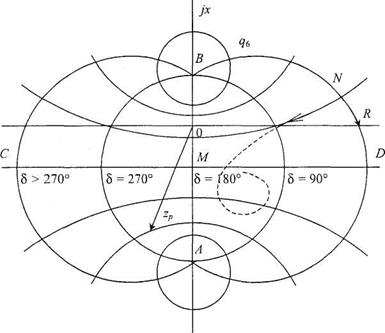
В соответствии с формулой (8. 14) можно построить диаграмму, на которой будет отмечено геометрическое место концов вектора Zp в зависимости от угла и от отношения q = Ес / Ег (рис. 8. 15). При построении диаграммы примем 
и Zc=Хс.
|
|
Рис. 8. 15. Диаграмма zp(q, )
При изменении угла от 0° до 360° выражение 
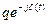соответствует вращающемуся вектору, конец которого вычерчивает окружность с центром в начале координат. Выражение 
соответствует окружности, центр которой смещен на 1, 0. В результате обращений этой окружности 1/(1-q 
) конец вектора Zp также будет перемещаться по окружности [18]. Не рассматривая здесь метод определения местоположения центра и радиуса обращения окружности, укажем лишь на порядок построения интересующей нас диаграммы.
На комплексной плоскости сопротивлений концы векторов Zг и Zc обозначим соответственно А и В. Отрезок АВ изображает вектор Z. Центры окружностей, по которым скользит конец вектора Zp при изменении угла , находятся на продолжении отрезка АВ вниз от точки А при q > 1 и вверх от точки В при q < 1. Положение центра и радиус окружностей определяется величиной q. На рис. 8. 15 показано несколько таких окружностей, причем 
. При q=1 радиус окружности равен бесконечности и окружность вырождается в прямую CD. Эта прямая проходит через середину
отрезка АВ (точка М) и перпендикулярна ему.
При постоянном значении угла , но переменном q конец вектора Zp также располагается на дугах окружностей, которые строятся следующим образом. Центры этих окружностей располагаются на прямой CD. Дополнительным условием для построения окружностей является условие их прохождения через точки А и В. Отрезок АВ может рассматриваться как дуга окружности бесконечно большого радиуса. Конец вектора Zp располагается на этом отрезке при угле = 180°. Геометрическим местом концов вектора Zp при < 180° являются дуги окружностей справа от отрезков АВ. При угле
|
|
|
> 180° конец вектора Zp располагается на дугах окружностей слева от отрезка АВ. Пользуясь диаграммой, можно определить сопротивление Zp при любых значениях угла и коэффициента q.
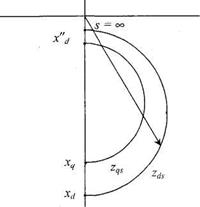
В предыдущих рассуждениях принято, что сопротивление генератора неизменно. В асинхронном режиме это сопротивление меняется и зависит от скольжения s. Это обстоятельство необходимо учитывать при построении диаграммы Zp (Ег, Ес, , s). На рис. 8. 16 показана зависимость сопротивления невозбужденного генератора от скольжения ротора s [14]. В силу несимметрии ротора сопротивление различно по продольной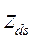 
, и поперечной 
осям. Рассмотрим сопротивление zds. При отсутствии скольжения турбогенератор замещается синхронным сопротивление xd. При скольжении 
машина представляется ее сверхпереходным сопротивление x" d. В области 0< s < 
геометрическим местом концов вектора сопротивления турбогенератора является характеристика, показанная на рис. 8. 15. В первом приближении она близка к полуокружности, построенной на отрезке xd - x" d, как на диаметре. В некоторых точках этой характеристики указаны значения скольжения, при котором определены сопротивления. Характеристика построена в области отрицательных значений х. Это обусловлено тем, что в данном случае измерение осуществляется с помощью реле сопротивления, для которого за положительное направление сопротивления принято направление от места установки реле к сети.
jx
| s = 0. 005 |
R
|
|
|
