 |
Каноническая форма задач линейного программирования (ЗЛП).
|
|
|
|
Лекция 1.
Математическая модель задачи линейного программирования.
Определение: Математической моделью (ММ) экономической задачи называется совокупность математических соотношений, описывающих рассматриваемый экономический процесс.
Задача линейного программирования (ЗЛП) заключается в изучении способов отыскания наибольшего или наименьшего значений линейной функции при наличии линейных ограничений.
Определение: Переменными ЗЛП называют величины х1, х2,.……,хn, которые полностью характеризуют экономический процесс. Их обычно записывают в виде вектора х= (х1, х2,.…..,хn)
Определение: Системой ограничений ЗЛП называется совокупность уравнений и неравенств, которым удовлетворяют нерешенные задачи и которые исследуют ограничение ресурсов или других экономических условий, например, условия положительности переменных.
Пусть ограничена задача совместной системой линейных неравенств с их переменными
,
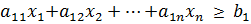Определение: Целевой функцией называют линейную функцию:
L=c1x1 + c2x2 +…+cmxn + 
,
которая характеризует качество выполнения задачи и экстремум, который требуется найти.
Определение: Допустимым решением (планом) ЗЛП называется любой n-мерный вектор x=(x 1, x 2, …, xn), удовлетворяющий системе ограничений и условиям неотрицательности. Множество допустимых решений ЗЛП образует область допустимых решений.
Определение: Оптимальным решением (планом) ЗЛП называется такое допустимое решение (план) задачи, при котором целевая функция достигает экстремума.
Для составления ММ необходимо:
1. Выбрать переменные задачи.
2. Составить систему ограничений.
3. Задать целевую функцию.
4. Указать экстремум который нужно найти.
|
|
|
Итак, задача линейного программирования имеет вид:
найти максимум (минимум) целевой функции
L=c 1 x 1 +c 2 x 2 +…+c m xn+c 0 →max(min)
в области допустимых решений,
,
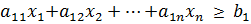Пример составления математических моделей экономических задач.
Задача использования ресурсов.
При производстве n видов продукции используется m видов ресурсов.
Известно:
1. b 1, b 2, …, b m –запасы ресурсов
2. 
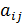, (i =1,2 …, m; j=1,2, …, n)- расход каждого i-того вида ресурса на изготовление единицы j-ой продукции
3. 
(j =1,2,…,n) - прибыль, полученная от реализации единицы j-ой продукции требуется составить план выпуска продукции, обеспечивающий максимальную прибыль
Обозначим вектор переменных задачи
x=(x1, x2, …,xn), где x j (j=1,2…,n) - объем выпуска j-ой продукции.
Учитывая, что 
- прибыль от реализации всего объема;
-затраты i-ого вида ресурса на весь объем выпуска j-ой продукции;
запишем математическую модель задачи. Также необходимо учитывать неотрицательность переменных задачи, так как объем выпуска не сможет быть отрицательным.
Таким образом, математическая модель имеет вид
L=c 1 x 1 +c 2 x 2 +…+c m xn+c 0 →max,
,
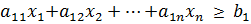Лекция 2.
Каноническая форма задач линейного программирования (ЗЛП).
Каноническая задача линейного программирования имеет вид:
L=c 1 x 1 +c 2 x 2 +…+c m xn+c 0 →max(min),
,
Она отличается от других задач тем, что её система ограничений является системой уравнений и все переменные неотрицательны.
Если имеются неравенства, то нужно перейти к равенствам, введя допустимые переменные.
Неравенство вида:
заменяется равенством
и неравенством
xn+1 ≥ 0,
а неравенство
заменяем равенством
и равенством
x n +1 ≥ 0.
Замечание. Дополнительные переменные вводят в целевую функцию с коэффициентами равными нулю.
Любая переменная x j, на которую не наложено условие неотрицательности, заменяется разностью двух других неотрицательных переменных
|
|
|
- 
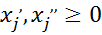
В канонической задаче целевая функция может как минимизироваться, так и максимизироваться. Для того, чтобы перейти от нахождения максимума к минимуму и наоборот, достаточно изменить знаки целевой функции.
Замечание. Полученная в результате этого задача имеет одно и то же оптимальное решение, а значения целевых функций отличается знаком.
Пример. Требуется привести к каноническому виду ЗЛП
L=3x 1 +x 2 +x 3 →min
На переменную х 1 условие неотрицательности не наложено.
Перейдем к задаче на отыскание максимума целевой функции. Для этого изменим знаки коэффициентов целевой функции, получим
L= - 3х 1 - х 2 - х 3 → max.
В целях превращения в уравнения второго и третьего неравенств системы ограничений, введем неотрицательные переменные х 4, х 5.
Заметим, что переменная х 4 вводится со знаком «+», т.к. неравенство 2 имеет вид «≤», переменная х 5 со знаком «-», т.к. неравенство 3 имеет вид «≥». В целевую функцию их введем с нулевыми коэффициентами.
Переменную х 1 заменим равенством
Х 1 = 
- 
, ≥ 0; ≥ 0.
Получаем ЗЛП в канонической форме
L = -3 
+ 3 
– х 2 – х 3 + ох 4 + ох 5 → max
- + 2х 2 + х 3 = 7
- - 
+ 2 
+ 
= 1
- 
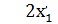+ х 2 – 2х 3 – х 5 = 5
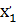≥ 0; ≥ 0; 
≥ 0; j = 1,2,3,4,5
|
|
|
