 |
Переход от канонической ЗЛП к симметричной.
|
|
|
|
Рассмотрим ЗЛП в канонической форме. Введем следующие обозначения
= (с 1, с 2, с 3, …, 
),
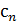а 11, а 12, …, а 1n
a 21, a 22, …, a 2n
………………..
… 
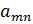
X= 
, 
= 
Определение: будем говорить, что ЗЛП имеет симметричный вид, если
L = С х →max
A * X ≤ 
x ≥ ⱷ
Или L = С х →min
A * X ≥ 
x ≥ ⱷ
При решении некоторых задач возникает необходимость перехода от канонической ЗЛП к симметричной.
Рассмотрим на примере переход.
Дана ЗЛП в канонической форме
L = 4x 1 – 5x 2 +x 3 + 2x 4 →max
3x 1 - 2x 2 + x 3 + 4x 4 = 6
-7x 1 +10x 2 + 3x 3 - 4x 4 = 2
≥ 0; j = 1,2,3,4
Методом Жордана – Гаусса приведем систему уравнений – ограничений к равносильной разрешенной. Одновременно разрешенные переменные исключим из целевой функции. Для этого в таблице решения задачи, наряду с коэффициентами уравнений системы ограничений, в дополнительной строке запишем коэффициенты целевой функции. В последнем столбце запишем свободный член целевой функции равный нулю.
При вычислениях учитываем, что разрешающий элемент в последней строке (в целевой функции) выбирать нельзя.
| Х1 | Х2 | Х3 | Х4 | В | |
| -7 | -2 -5 | -4 | |||
| -16 | -2 -3 | -16 -2 | -16 -6 | ||
| -1 |
-3 | -1 -2 | -1 -6 | ||
| -1 -2 | -1 -5 | -1 -9 |
Число -9, полученное в последнем столбце последней строки необходимо записать в целевую функцию с противоположным знаком. В результате данных преобразований задача принимает вид:
L= -2x 1 + 0x 2 + 0x 3 - 5x 4 + 9→max
x 1 + x 3 +2x 4 =4
-x 1 +x 2 x 4 =-1
, j =1,2,3,4.
Так как переменные х 2,х 3 – неотрицательные, то отбросив их, можно записать задачу в симметричном виде.
L = -2x, -5x 4 + 9 
max
х 1 + 2х 4 ≤ 4
-х 1 - х 4 ≤ -1
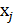≤ 0, j = 1,4
Теория двойственности
Любой задаче линейного программирования, называемой исходной или прямой. Можно поставить в соответствие другую задачу, которая называется двойственной или сопряженной. Обе эти задачи образуют пару двойственных (или сопряженных) задач. Каждая из этих задач является двойственной к другой задаче рассматриваемой пары.
В теории двойственности используются четыре пары двойственных задач (приведем их в матричной форме записи): Симметричные задачи
|
|
|
Исходная задача Двойственная задача
Правила составления двойственных задач.
· Во всех ограничениях исходной задачи свободные члены должны находится в правой части, а члены с неизвестными – в левой.
· Ограничения-неравенства исходной задачи должны быть записаны так, чтобы знаки неравенств у них были направлены в одну сторону.
· Если знаки неравенств в ограничениях исходной задачи «
», то целевая функция 
должна максимизироваться, а если «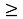
», то минимизироваться.
· Каждому ограничению исходной задачи соответствует неизвестное в двойственной задаче; при этом неизвестное, отвечающее ограничению-неравенству, должно удовлетворять условию неотрицательности, а неизвестное, отвечающее ограничению-равенству, может быть любого знака.
· Целевая функция двойственной задачи имеет вид 
, где 
– свободный член целевой функции F(X) исходной задачи, 
– свободные члены в ограничениях исходной задачи, при этом 
– свободный член именно того ограничения исходной задачи, которому соответствует неизвестная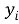 
, а 
– неизвестные в двойственной задаче.
· Целевая функция Z(Y) двойственной задачи должна оптимизироваться противоположным по сравнению с F(X) образом, т.е. если 
, то 
и наоборот.
· Каждому неизвестному 
, 
исходной задачи соответствует ограничение в двойственной задаче. Совокупность этих n ограничений образует систему ограничений двойственной задачи. Все ограничения двойственной задачи имеют вид неравенств, свободные члены которых находятся в правых частях, а члены с неизвестными 
. Все знаки неравенств имеют вид «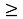», если 
«» если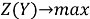 
.
|
|
|
Коэффициенты, с которыми неизвестные входят в ограничение, соответствующее неизвестному , совпадают с коэффициентами при этом неизвестном в ограничениях исходной задачи, а именно: коэффициент при уi совпадает с тем коэффициентом при хj, с которым хj входит в ограничение исходной задачи, соответствующее неизвестному yi.
Первая теорема двойственности
Теоремы двойственности позволяют установить взаимосвязь между оптимальными решениями пары двойственных задач, можно или найти оптимальное решение другой задачи, не решая ее, или установить его отсутствие. Возможны следующие случаи:
· обе задачи из пары двойственных задач имеют оптимальные решения;
· одна из задач не имеет решения ввиду неограниченности целевой функции, а другая не имеет решения ввиду несовместности системы ограничений
Теорема 3. Если одна из пары двойственных задач имеет оптимальное решение, то и двойственная к ней имеет оптимальное решение, причем значения целевых функций задач на своих оптимальных решениях совпадают.
Если одна из пары двойственных задач не имеет решения ввиду неограниченности целевой функции, то другая не имеет решения ввиду несовместности системы ограничений.
Вторая теорема двойственности
Пусть имеется симметричная пара двойственных задач
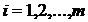
Теорема. Для того чтобы допустимые решения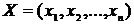 
являлись оптимальными решениями пары двойственных задач, необходимо и достаточно, чтобы выполнялись следующие равенства:
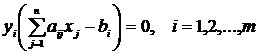
Иначе, если при подстановке оптимального решения в систему ограничений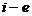 
ограничение исходной задачи выполняется как строгое неравенство, то 
координата оптимального решения двойственной задачи равна нулю, и, наоборот, если координата оптимального решения двойственной задачи отлична от нуля, то 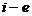ограничение исходной задачи удовлетворяется оптимальным решением как равенство.
Двойственные задачи.
Составить задачу, двойственную к данной:
L(x)=5x 1 +2x 2 +3x 3 →min
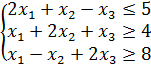
x j ≥ 0; j=1,2,3
Решение:
Умножим первое ограничение неравенства на -1. Задача примет вид исходной задачи симметричной пары двойственных задач:
|
|
|
| Y1 Y2 Y3 |
x j ≥ 0; j=1,2,3
Умножим правые части ограничений на соответствующие переменные двойственной задачи и сложим их, получим целевую функцию:
F(y) = -5y 1 +4y 2 +8y 3 →max
Функция F(y) максимизируется, так как целевая функция исходной задачи минимизируется.
Умножим коэффициенты приx1 в системе ограничений на соответствующие переменные двойственной задачи и сложим их, получим -2у 1 +1∙у 2 +1∙у 3. Данная сумма меньше или равна коэффициенту при х1в целевой функции -2у 1 + у 2 + у 3 ≤ 5. Неравенство имеет вид «≤», потому что целевая функция двойственной задачи максимизируется. Аналогично составляются еще два ограничения двойственной задачи (соответствуют переменным х 2, х 3):
-1∙у 1 +2у 2 -1∙у 3 ≤ 2
1∙у 1 -1∙у 2 +2у 3 ≤ 3
Все переменные двойственной задачи удовлетворяют условию неотрицательности, потому что все ограничения исходной задачи- неравенства.
Окончательно двойственная задача имеет вид:
F(y)=-5y 1 +4y 2 +8y 3 →max
x j ≥ 0; j =1,2,3
|
|
|
