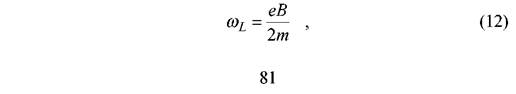Магнитные моменты электронов и атомов

 

Магнетиками называются вещества, способные приобретать во внешнем магнитном поле собственное магнитное поле, т.е., намагничиваться. Магнитные свойства вещества определяются магнитными свойствами электронов и атомами (молекулами) ве­щества. По магнитным свойствам магнетики подразделяются на три основные группы: диамагнетики, парамагнетики и ферромаг­нетики.

Рассмотрим движение электрона по орбите в атоме. Его можно считать эквивалентным некоторому замкнутому контуру с током (орбитальный ток). Такой контур будет обладать магнитным моментом, значение которого будет определяться профилем кон­тура и величиной силы тока. Если поверхность контура площа­дью S плоская (орбита электрона), все нормали к поверхности имеют одинаковое направление. Магнитный момент такого “вит­ка” с током называется орбитальным магнитным моментом электрона. Он равен:

где I = en - сила тока, e – абсолютная величина заряда элек­трона, n - число оборотов электрона по орбите в единицу времени

ни, S - площадь орбиты электрона, n –

единичный вектор нормали к площади

S.

Электрон, движущийся по орбите,

имеет орбитальный момент импульса

L_e. Орбитальный магнитный момент

Здесь m – масса электрона. Величина g называется гиромаг­нитным отношением орбитальных моментов.

пропорционален орбитальному момен­ту

 

Векторы p_m и L_e направлены в противоположные стороны и перпендикулярны к плоскости орбиты электрона (рисунок 1.).

Кроме названных выше величин электрон обладает собственным                                                                                  

 моментом импульса L_es, который называется спином элек­трона. Абсолютная величина спина электрона равна:

 

 

Важнейшей особенностью спина электрона является наличие

только двух его проекций на направление вектора B индукции

Спину электрона L_es соответствует спиновой магнитный момент p_ms пропорциональный спину и направленный в противо­положную сторону:

Величина g_s называется гиромагнитным отношением спино­вых моментов:

Проекция спинового магнитного момента электрона p_msB на направление магнитного поля

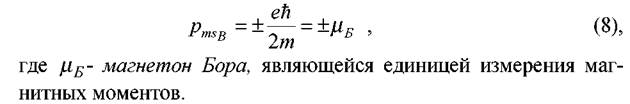
Соотношения (1) – (8) справедливы для каждого из Z электро­нов в атоме. Число Z совпадает с порядковым номером химиче­ского элемента в периодической системе Менделеева.

В атоме, содержащем Z электронов, их орбитальные магнит-r r

ные моменты p_m и орбитальные моменты импульса L_es склады­ваются векторно. В результате каждый атом может быть охарактеризован орбитальным магнитным моментом P_m и орбитальным

 

Орбитальным магнитным моментом Pm атома называется векторная сумма орбитальныхr магнитных моментов pm всех его электронов:

Орбитальным моментом импульса L атома называется век

моментом импульса L.

торная сумма орбитальных моментов импульса L_e всех Z электронов 

Атомные моменты Pm и L связаны соотношением:

 

 

где g – гиромагнитное отношение (3).

Все вещества, с которыми нам приходится иметь дело, состоят из атомов. Поведение вещества в целом под воздействием каких-либо физических факторов будет определяться взаимодействием составляющих его частиц, то есть, атомов с этим физическим фактором. Рассмотрим поведение атома, имеющего Z электро­нов, в магнитном поле.

3.2 Атом в магнитном поле

 

Если вещество находится во внешнем магнитном поле, то в пределах атома можно считать магнитное поле однородным. Это следует из малости линейных размеров атома. Предположим, что электрон в атоме движется по круговой орбите, плоскость которой перпендикулярна к вектору индукции B магнитного поля. Действие на электрон силы Лоренца F_Л приведет к уменьшению силы притяжения электрона к ядру. Центростремительная сила окажется равной разности F_e - F _Л, где F_e - кулоновская сила притяжения электрона к ядру (рис. 2.). В результате изменится угловая скорость w движение электрона по круговой орбите. Она станет отличной от той, которую электрон имел в отсутствии внешнего магнитного поля.

Если внешнее магнитное поле переменное, то изменение угло­вой скорости движения электрона происходит в процессе нарас­тания магнитного поля, в которое вносится атом. Нарастание магнитного поля, действующего на атом, происходит за конечное время.

При этом возникает индукционное вихревое электрическое поле

действующее на электрон в атоме. Напряженность E этого                                                    

поля направлена по касательной к орбите электрона, а сила действующая на электрон, равна F = eE.

При произвольном расположении орбиты электрона относительно вектора B, орбитальный магнитный момент p_m электро­на (1) составляет угол a с направлением магнитного поля (рису­нок 3.). В этом случае орбита прецессирует вокруг направления вектора B. Это означает, что вектор p_m, перпендикулярный к плоскости орбиты, сохраняя неизменный угол a наклона к полю,

 

вращается вокруг направления B с угловой скоростью w_L:

 

        Это вращение вектора p_m вокруг направления B при неизмен­ном угле     a называется ларморовской прецессией. Величина w_L называется угловой скоростью ларморовской прецессии.

Влияние магнитного поля на орбиту электрона отражено в тео­реме Лармора: единственным результатом влияния магнитного поля на орбиту электрона в атоме является прецессия орбиты и r вектора p_m с угловой скоростью w_L вокруг оси, проходящей через ядро атома и параллельной вектору B индукции магнитного поля.

Прецессионное движение орбиты приводит к появлению до­полнительного орбитального тока D I _орб (рисунок 3) и соответст­вующего ему наведенного орбитального магнитного момента

D p_m, модуль которого равен:

 

 

где S _^ - площадь проекции орбиты электрона на плоскость,

 

перпендикулярную к направлению B. Вектор p_m направлен

r

противоположно вектору магнитной индукции B:

 

Общий, наведенный внешним магнитным полем, орбитальный

магнитный момент D P_m атома

 

 

где Z – число электронов в   атоме, средняя площадь проекции орбит электронов в атоме на плоскость, перпендикулярную к направлению вектора B.

Таким образом, электронные орбиты атома под действием внешнего магнитного поля совершают прецессионное движение, которое эквивалентно круговому току. Так как этот микроток ин­дуцирован внешним магнитным полем, то, согласно правилу Ленца, у атома появляется составляющая магнитного поля, на­правленная противоположно внешнему полю, наведенные со­ставляющие магнитных полей атомов (молекул) складываются и образуют собственное магнитное поле вещества, ослабляющее внешнее магнитное поле. Этот эффект получил название диамаг­нитного эффекта. Вещества, у которых магнитные моменты ато­мов (или молекул) в отсутствие внешнего магнитного поля равны нулю и намагничивающиеся во внешнем магнитном поле про­тив направления поля называются диамагнетиками.

В отсутствие внешнего магнитного поля диамагнетик не­магнитен, поскольку в данном случае магнитные моменты элек­тронов взаимно компенсируются, и суммарный магнитный мо­мент атома равен нулю. Диамагнетиками являются многие ме­таллы (Bi, Ag, Au, Cu), большинство органических соединений, смолы, углерод и т.д.

Наряду с диамагнитными веществами существуют и такие вещества, у которых в отсутствие внешнего магнитного поля магнитные моменты электронов не компенсируют друг друга, и атомы (или молекулы) в отсутствии внешнего магнитного поля всегда обладают некоторым постоянным магнитным моментом P_m. Однако вследствие теплового движения молекул их магнит­ные моменты ориентированы беспорядочно. Поэтому такие ве­щества магнитными свойствами не обладают. Их называют па­рамагнетиками.

При внесении парамагнетика во внешнее магнитное поле

магнитные моменты атомов (молекул) прецессируют вокруг век-r

тора B с ларморовской угловой скоростью w_L, устанавливается

преимущественная ориентация собственных магнитных моментов атомов P_mi по направлению внешнего поля (полной ориен­тации препятствует тепловое движение атомов). Таким образом, парамагнетик намагничивается, создавая собственное магнитное поле, совпадающее по направлению с внешним полем и усили­вающее его. Этот эффект называется парамагнитным. При ослаб­лении внешнего магнитного поля до нуля ориентация магнитных моментов вследствие теплового движения нарушается и парамаг­нетик размагничивается. Парамагнетиками являются редкозе­мельные элементы, Pt, Al и т.д. Диамагнитный эффект наблюдается и в парамагнетиках, но он значительно слабее парамагнитно­го и поэтому остается незаметным.

 

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: