 |
Статистическая обработка результатов имитационного эксперимента
|
|
|
|
№ 4(при влиянии напряжения питания)
Расчеты
Математическое ожидание-величина, относительно которой рассеиваются результаты отдельных наблюдений.
а) Расчет математического ожидания
= 
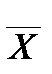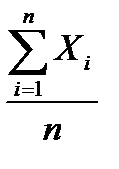= 278,6038 0С
Дисперсия- характеризует степень рассеивания результатов отдельных наблюдений вокруг математического ожидания.
б) Расчет дисперсии
D = S2 = 
= 47,038860С2
в) Расчет среднеквадратического отклонения результата наблюдений
= S = 
= 
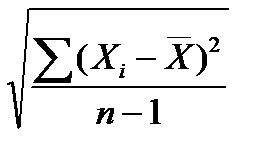= 6,858488 0С
г) Расчет среднеквадратического отклонения результата измерений
= 0,370364 0С
2.3.2 Диаграмма распределения температуры
а) R = Xmax – Xmin
R = 29,036 0С
б) r = 1+3.32*lg(n) (n=50-количество измерений)
r = 1+3.32*lg50
r = 7
= 4,1480С
Для построения гистограммы составим таблицу:
j – номер интервала
nj – число значений, попавших в интервал
Таблица 4-Зависимость между частотой попадания в интервал случайной величины и номером интервала
| j | Xj 0С | Nj | ||
| ||||
| 267,259 | ||||
| 271,407 | ||||
| 275,555 | ||||
| 279,703 | ||||
| 283,851 | ||||
| 287,999 |
Далее строим график зависимости Xj(nj)
По гистограмме определено, что закон распределения результатов наблюдений измеряемой величины- равномерный.
Результат
А) Результат наблюдений: 
Где k -квантильный множитель, т.к. закон распределения равномерный (определено по гистограмме), k= 1,73.
= 
Б) Результат измерений: 
=0,95
= 
Затем на закладке «Условия эксплуатации» выбрали пункт «Влияние всех факторов».
Затем произвели имитационный эксперимент № 5- при влиянии всех факторо
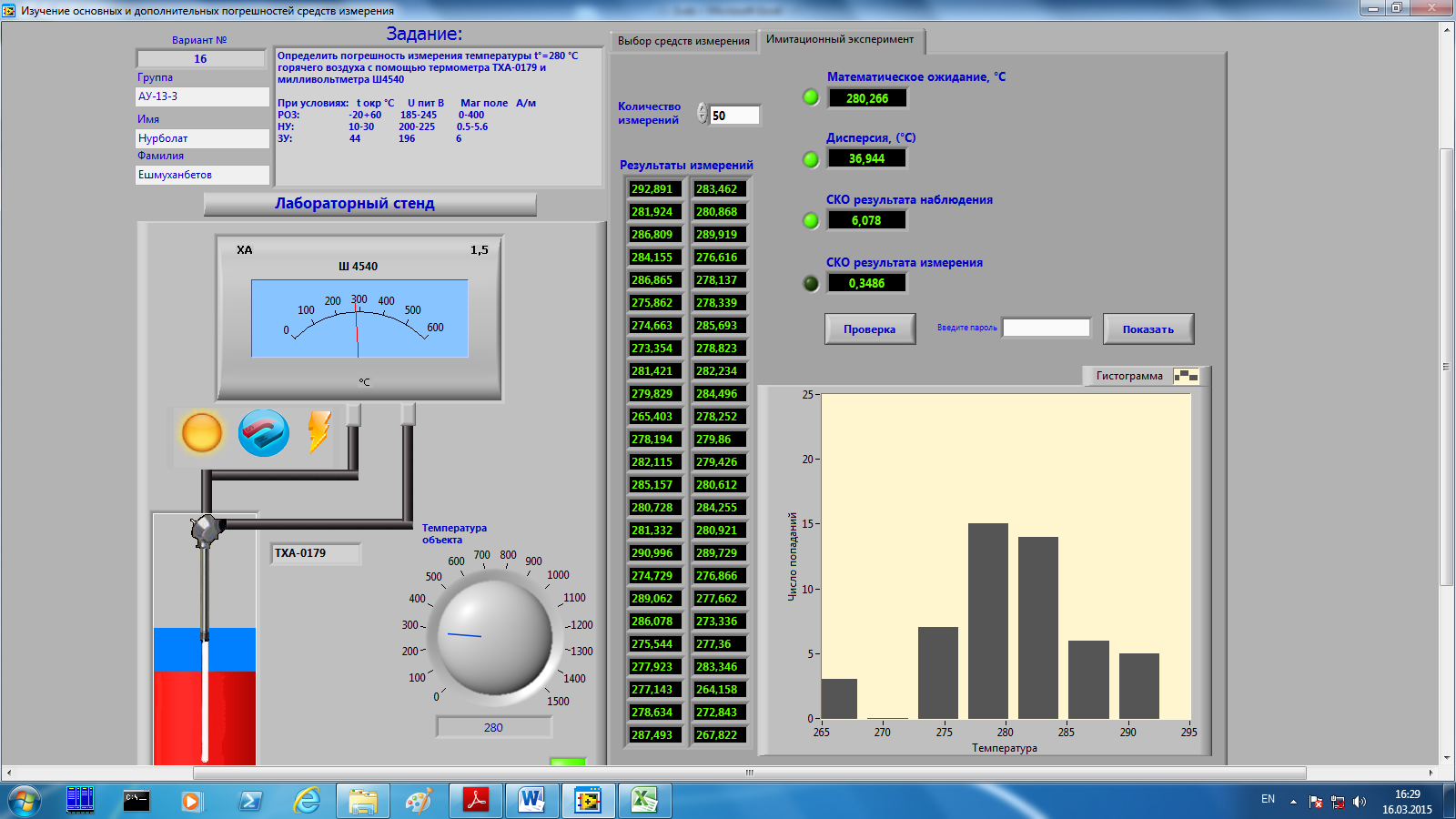
Статистическая обработка результатов имитационного эксперимента
№ 5(при влиянии всех факторов)
Расчеты
Математическое ожидание-величина, относительно которой рассеиваются результаты отдельных наблюдений.
|
|
|
а) Расчет математического ожидания
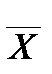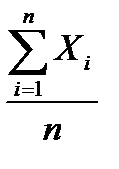= = 280,2668 0С
Дисперсия- характеризует степень рассеивания результатов отдельных наблюдений вокруг математического ожидания.
б) Расчет дисперсии
D = S2 = = 36,94403 0С2
в) Расчет среднеквадратического отклонения результата наблюдений
= S = = = 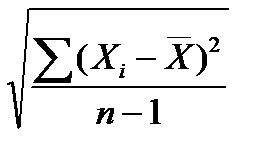6,07816 0С
г) Расчет среднеквадратического отклонения результата измерений
= 0,348659 0С
2.3.2 Диаграмма распределения температуры
а) R = Xmax – Xmin
R = 28,7330С
б) r = 1+3.32*lg(n) (n=50-количество измерений)
r = 1+3.32*lg50
r = 7
= 4,104714
0С
Для построения гистограммы составим таблицу:
j – номер интервала
nj – число значений, попавших в интервал
Таблица 5-Зависимость между частотой попадания в интервал случайной величины и номером интервала
| j | Xj 0С | Nj | |||
| |||||
| 268,2627 | |||||
| 272,3674 | |||||
| 276,4721 | |||||
| 280,5769 | |||||
| 284,6816 | |||||
| 288,7863 |
Далее строим график зависимости Xj(nj)
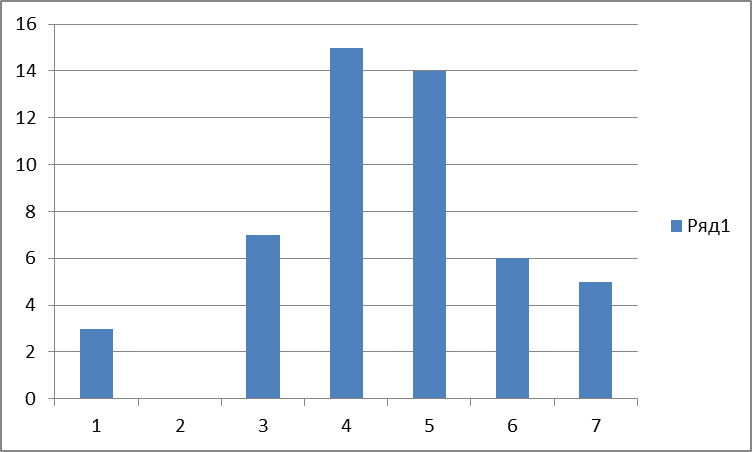
По гистограмме определено, что закон распределения результатов наблюдений измеряемой величины-нормальный.
Результат
А) Результат наблюдений:
Где k -квантильный множитель, т.к. закон распределения нормальный(определено по гистограмме), k= 2,01.
= 
Б) Результат измерений: 
= 
Расчет основной и дополнительных погрешностей средств измерений
Расчет погрешности средства измерений в нормальных условиях эксплуатации
Допускаемое отклонение (погрешность) градуировки первичного преобразователя (
) согласно зависит от его типа и заданы в технических характеристиках первичного преобразователя.
Предел допускаемой основной абсолютной погрешности показаний вторичного прибора определяется по формуле
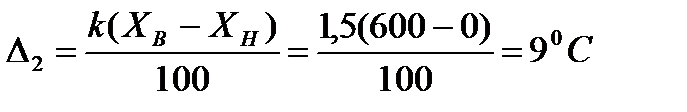
где 
- класс точности вторичного прибора;
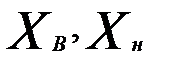-верхняя и нижняя границы диапазона измерения вторичного прибора, мВ(для милливольтметра или потенциометра) или Ом(для моста или логометра).
|
|
|
Предельная абсолютная основная погрешность показаний измерительного канала в нормальных условиях определяется по формуле
.
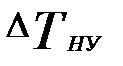=9,84885 0С
|
|
|
