 |
§3.4.Статистический оператор (матрица плотности) и корреляционные функции.
|
|
|
|
Известно, что в квантовой механике каждой физической величине A соответствует оператор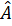 
. Наблюдаемыми на опыте значениями этой величины являются квантово - механические средние
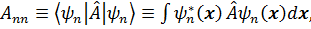(3. 33)
где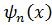 
– ортонормированные собственные функции гамильтониана системы:
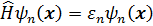. (3. 34)
В (3. 34) индекс n нумерует состояния,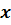 
- совокупность независимых координат, 
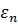- соответствующие собственные значения. Если оператор 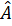коммутирует с гамильтонианом 
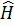, то система 
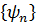является системой его собственных функций, а наблюдаемые значения (3. 33) будут собственными значениями оператора .
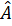В квантовой статистической механике под наблюдаемой величиной понимается её среднее статистическое значение, которое определяется выражением
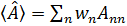. (3. 35)
В этом выражении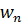 
- вероятность обнаружить систему в состоянии n, или статистический вес этого состояния. Очевидно, что должно выполняться условие
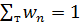, (3. 36)
которое означает, что полная вероятность всех вантовых состояний равна единице.
Введем квантово-статистический оператор (матрицу плотности), который в матричном представлении (x - представлении) имеет вид
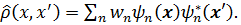(3. 37)
Из ортонормированности волновых функций и (3. 37) следует, что
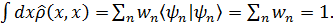(3. 38)
Запишем теперь выражение для среднего значения оператора 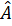при помощи
матрицы плотности (3. 37):
= 
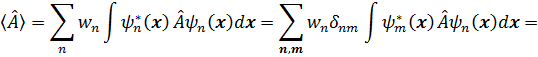
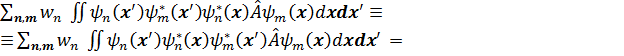
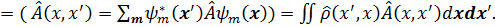(3. 39)
Здесь мы ввели матричное x - представление для оператора 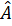. Выражение (3. 39) обычно записывают в виде
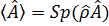, (3. 40)
|
|
|
где шпур берется по координатам x. Последняя запись удобна тем, что она не зависит от представления операторов 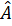и 
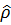. В частности, под шпуром можно понимать сумму по собственным состояниям
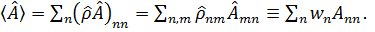(3. 41)
В квантовой статистике это представление (n-представление) наиболее удобно. Распределение вероятностей 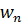для случая статистического равновесия выбирают в виде канонического распределения Гиббса:
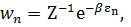(3. 42)
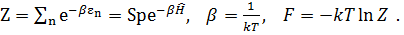(3. 43)
Поэтому, в x – представлении статистический оператор в случае статистического равновесия даётся выражением
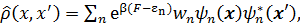(3. 44)
а сам оператор
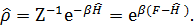(3. 45)
Независимыми переменными в каноническом ансамбле Гиббса являются температура T, объём V и число частиц N. Поэтому, при суммировании по квантовым состояниям необходимо учитывать только состояния с заданным числом N, что существенно затрудняет процедуру взятия шпура. Чтобы не связывать себя условием постоянства числа частиц, удобно перейти к большому каноническому ансамблю, где независимыми переменными являются T, V и химический потенциал 
. Для этого в гамильтониан вводится дополнительный член
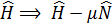, (3. 46)
и накладывается дополнительное условие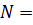 
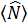, из которого определятся химический потенциал . В этом случае статистический оператор имеет вид
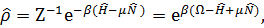(3. 47)
где
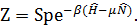(3. 48)
В (3. 47) величина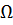 
называется термодинамическим потенциалом системы в переменных T, V и . Теперь в формулах для статистических средних значений можно суммировать по всем состояниям без ограничения на число частиц в системе.
Рассмотрим ансамбль систем с гамильтонианом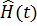 
, зависящим от времени. Матрица плотности в этом случае определяется выражением
|
|
|
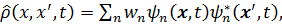(3. 49)
где 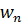не зависят от t. Функции 
являются решениями нестационарного уравнения Шредингера, удовлетворяющими начальному условию
(3. 50)
Таким образом,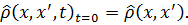 
Используя уравнение Шредингера в матричном виде
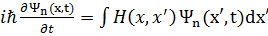, (3. 51)
где
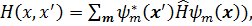(3. 52)
и свойство эрмитовости гамильтониана 
, можно получить уравнение движения статистического оператора в матричной форме
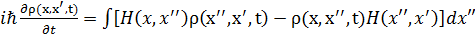. (3. 53)
Это уравнение называется квантовым уравнением Лиувилля. В операторной форме оно имеет вид
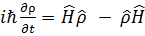. (3. 53)
При помощи оператора 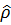можно вычислить среднее от произведения нескольких операторов
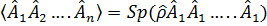. (3. 54)
Эти средние значения определяют корреляцию одной или нескольких физических характеристик системы частиц и называются корреляционными функциями.
В квантовой теории особое значение имеет корреляционная функция двух операторов
.
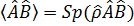В случае равновесия
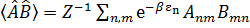. (3. 55)
Использование статистического оператора 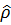обеспечивает максимально полное статистическое описание квантовой системы.
Литература
1. А. Н. Матвеев, Молекулярная физика, М., Высшая школа, 1981.
2. Д. В. Сивухин, Курс общей физики, том 2 “Термодинамика и молекулярная физика”, М., Наука, 1979.
3. Ландау Л. Д., Лифшиц Е. М., Теоретическая физика, том 5 “ Статистическая физика”, Часть 1, М., Физматлит, 2001.
4. Р. Фейнман, Статистическая механика, М., “Мир”, 1975.
|
|
|
