 |
Отверждение (вулканизация).
|
|
|
|
5.3.1. Общие сведения.
— Этот процесс тесно связан с термообработкой материала, и, поскольку изделия могут иметь достаточно солидные габариты, а теплопроводность полимера низкая, могут иметь место значительные градиенты температур по толщине изделия. Это ведет к тому, что процесс формирования окончательной структуры в различных участках изделия происходит с различной скоростью.
— Для ориентировочных расчетов в таких случаях используется правило Вант-Гоффа, согласно которому при повышении температуры на 10 град. Скорость реакции увеличивается в 2¸4 раза.
— Отношение констант скоростей k реакций, проведенных при двух температурах, отличающихся на 10К, называется температурным коэффициентом скорости реакции:
 . .
| (1) |
— При проведении ориентировочных расчетов используется допущение, позволяющее считать температурный коэффициент равным двум и не зависящим от времени. Как же обстоит дело на самом деле?
— Зависимость скорости реакции от температуры, как известно, определяется уравнением Аррениуса:
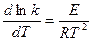 , ,
| (2) |
где E – энергия активации, рассчитанная на NA (число Авогадро) актов реакции; R – универсальная газовая постоянная. Энергия активации равна средней избыточной энергии молекул, вступающих в элементарный акт реакции. Приближенно ее можно отождествлять с величиной энергетического барьера для данной реакции, т.е. минимальной энергией (по отношению к энергии молекул при 0К), при которой акт реакции становится возможным. Энергия активации в первом приближении не зависит от температуры, поэтому интегрирование дает:
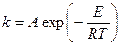 , ,
| (3) |
где A –величина, в том же приближении, не зависящая от температуры, называемая предэкспоненциальным или частотным фактором (A=k при T®¥).
|
|
|
— Воспользовавшись уравнением (3), получим:
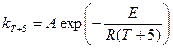 и и 
| (4) |
— Подставив соотношения (4) в формулу (1), получим:
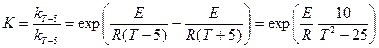 . .
| (5) |
Или
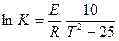 . .
| (6) |
— Выражение (6) показывает, что температурный коэффициент скорости реакции уменьшается с увеличением температуры. При увеличении температуры на 150К температурный коэффициент уменьшается приблизительно в 1.6 раза.
— Выясним теперь, как сказывается применение правила Вант-Гоффа на результатах вычисления степени превращения.
— Для этого воспользуемся распространенным в технологии методом приращения эквивалентных времен.
— В соответствии с этим методом для оценки скорости процесса используется показатель интенсивности процесса J:
 , ,
| (7) |
где T – температура в какой-либо точке изделия, в общем случае зависящая от времени; T0 – температура, ниже которой процесс идет с пренебрежимо малой скоростью; 10=(T+5)–(T–5). Интенсивность процесса – величина безразмерная.
— Для оценки степени завершенности процесса используется показатель эффективности (эффект процесса):
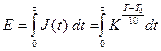 , ,
| (8) |
Нетрудно видеть, что величина E имеет размерность времени.
— В рассматриваемую процедуру расчета некоторую неопределенность вносит наличие температуры T0. Для исключения этого фактора вводится показатель степени завершенности процесса – эквивалентное время. Это продолжительность термообработки изделия в неизотермических условиях, по своему эффекту (степени завершенности) эквивалентное продолжительности термообработки в изотермических условиях при стандартной эквивалентной температуре, традиционно равной температуре кипения воды при давлении 2, 3, 4 и т.д. атмосферы (такое ограничение не должно неукоснительно выполняться, поскольку никак не отражается на результатах расчета).
— В соответствии с вышеизложенным, эквивалентное время определяется следующим соотношением:
|
|
|
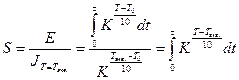 , ,
| (9) |
где Tэкв. = 120, 133, 143 и т.д. (в оС) – эквивалентная температура.
— Или через энергию активации:
 . .
| (10) |
— При постоянной температуре интенсивность процесса также равна постоянной величине, а эквивалентное время линейно растет во времени
5.3.2. Оптимизация процесса вулканизации (отверждения).
— При термообработке изделий внутри них возникают неизотермические условия T(t), определяемые экспериментально или расчетным путем. В зависимости от температурных условий по толщине изделия достигается различная степень завершенности процесса.
— Количественное аналитическое описание всей совокупности элементарных процессов, происходящих при образовании сетки в многокомпонентной системе, не представляется возможным. Характер реакции (структурирование, деструкция), тип образуемых связей и зависимость от них разных свойств композиционного материала сильно изменяется при варьировании состава и температурных условий протекания реакции. Суммарные кинетические кривые, описывающие зависимость "свойство F – продолжительность процесса", могут монотонно и нелинейно возрастать и иметь максимумы и минимумы. Поэтому, если реакции приписывать какой-то порядок, например, первый, то константы скорости реакции оказываются функциями, как температуры, так и степени завершенности процесса (времени), т.е. являются кажущимися или так называемыми эффективными характеристиками. Направление изменения константы указывает на преобладание процессов структурирования или деструкции, а величина (переменная во времени) – на интенсивность процессов.
— Для достаточно большой группы термореактивных материалов применима следующая закономерность изменения эффективной константы скорости реакции k от продолжительности процесса t и температуры T:
 , ,
| (11) |
где k0, b, w, E – константы, определяемые экспериментально, R – универсальная газовая постоянная.
— Если учесть, что интенсивность процесса I – это отношение констант скоростей при исследуемом T(t) и каком-либо стандартном процессе (T0=const), то для неизотермического режима T(t) по достижении заданного уровня свойств F при k=k(T(t)) имеется эквивалентное (в смысле получения того же уровня F) времяt=Sэкв термообработки в изотермическом режиме T=Tэкв=const, и тогда для малых w и bw (w«b) находим из (11):
|
|
|
 . .
| |
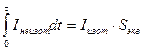 . .
| |
 . .
| |
 . .
| |
 . .
| |
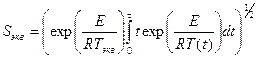 . .
| (12) |
— Для получения аналитического выражения T(t) используем приближение – "эквивалентную" многослойной системе однородную неограниченную пластину толщиной l, температуропроводностью a при переменных по времени температурах границы j1(t) и j2(t) соответственно координатам x по толщине при x=0 и x=l. Функции j1(t) и j2(t) характеризуют заданный режим термообработки.
— Оптимизация режима заключается в выборе таких значений j1(t) или j2(t), при которых достигается максимально возможная равномерность степени завершенности процесса, выражаемая уровнем F свойства материала изделия по толщине. Это удовлетворяет минимуму разностей |Fx=0–Fmin| и |Fx=l–Fmin|. Индексы x=0 и x=l указывают поверхность, индекс min – наименее прогреваемый участок.
— Поскольку тепловой поток в изделии подбирается симметричным (с учетом толщины и теплофизических характеристик элементов изделия), то Fmin наблюдается при минимальной температуре, определяемой на стадии регулярного режима.
— Сформулированная выше задача решается численными методами
— При проведении расчетов необходимо учесть, что энергия активации E, определяемая по кинетическим изотермическим кривым "свойство F – время t " фактически зависит от выбранного свойства. Если определять степень завершенности процесса по комплексу свойств в зависимости от назначения изделия при его эксплуатации, то, очевидно, следует каким-то путем установить эффективное значение энергии активации Eэфф, получаемое по Ej (j=1, 2,…, m), где m – число значащих показателей свойств, j – одно из комплекса свойств. Усреднение может производиться с учетом значимости каждого свойства. В первом приближении можно считать Eэфф как среднее арифметическое.
— Эффективный коэффициент температуропроводности aэкв находится для однородной эквивалентной, приведенной к многослойной пластине, толщиной dэкв и составленной из слоев толщинами dj с температуропроводностью: aj:
|
|
|
 . .
| (13) |
— Вместо среднего арифметического значения Eэфф можно взять полусумму крайних (минимального и максимального), т.е. лимитирующих процесс значений Ej.
— В последующем с учетом возможностей технологического оборудования, конфигурации изделия, более сложной, чем в пластине, распределения температур, режимы ji(t) уточняются путем решения близких вариантов распределения температур T(t).
— Для этих целей широко используется метод конечных элементов (МКЭ). МКЭ представляет собой разновидность способов приближенного численного интегрирования дифференциальных уравнений движения сплошной среды, позволяющих определить вид непрерывных функций, описывающих поле некоторых скалярных или векторных величин (давлений, скоростей, температур). При использовании этого метода непрерывная область или тело подразделяется на конечное число подобластей. Каждый элемент может иметь свой собственный размер и свою форму, которые выбирают так, чтобы они наилучшим образом соответствовали форме и размерам тела, Этот метод МКЭ отличается от метода конечных разностей, при котором используется сетка с ячейками одинакового размера, описываемыми теми же координатами, что и тело. Точки пересечения кривых, ограничивающих соседние элементы, называются узлами. Значения переменных, вычисленные в узлах, дают искомое решение. Обычно конечные элементы в двухмерных задачах имеют треугольную, прямоугольную или четырехугольную форму; при решении трехмерных задач используют элементы, имеющие форму прямоугольных призм и тетраэдров. Внутри каждого элемента подбирается интерполяционная функция, описывающая изменение определяемого параметра. Выбранные аппроксимирующие функции называются пробными функциями или пространственными изменяемыми моделями.
— Критерием оптимизации может служить не только максимальная равномерность степени завершенности процесса по толщине изделия при условии ограничения достижения необходимой степени завершенности процесса на лимитирующем участке, но и другие значимые факторы, уровень которых при данном критерии задается (например, уровень исходных температур, уровень температур на границе, их распределение, продолжительность процесса). Если оптимальный характер изменения температур на границе установлен, можно попытаться оптимизировать другие теплотехнические параметры при заданном составе и конструкции изделия. Естественно, состав композиции и конструкция изделия выбираются, прежде всего, исходя из соображений оптимальности свойств изделия в условиях его эксплуатации, хотя толщина и конфигурация изделия, его теплофизические свойства и кинетические параметры процесса вулканизации (отверждения) определяют режимы термообработки, и их не в ущерб технологичности композиций и свойствам материала в эксплуатации можно варьировать, сообразуясь с режимами термообработки. Особенно это касается кинетических характеристики допустимых температур термообработки.
|
|
|
— Температуры, их распределение, продолжительность процесса – это прямые параметры режима. По ним можно определить такой критерий оптимизации, как, например, тепловой поток, обеспечивающий выбранные режимы (в том числе и оптимизированные).
— Поиск тепловых потоков представляет интерес в том случае, если их можно распределить по контуру обогреваемого изделия соответственно переменным толщинам изделия. Так, при зонном обогреве пресс-форм представляется целесообразным по-разному обогревать различные поверхности изделия.
— Предварительную оценку соотношения тепловых потоков и соответствующих мощностей внешних источников тепла (электронагревателей, индукторов, энтальпии греющего пара, подаваемого по зонам), можно получить при использовании модели "эквивалентной" однородной пластины для температурного поля T(x, t) в пластине.
— Может быть реализовано оптимальное управление процессом на основе минимизации продолжительности процесса. При этом изыскивается оптимизирующее температурное воздействие U (режим), на которое наложено ограничение Umin£U£Umax.
— Для конечно-разностного описания кинетического неизотермического процесса можно провести оптимизацию режима путем динамического программирования. Критерием оптимальности является минимум различия в F на поверхности изделия Fпов и на лимитирующем участке Fлим при ограничении Fпов£Fв, £Fлим (Fн, Fн – верхний и нижний пределы норм показателей) за заданную продолжительность процесса t=tв. При динамическом программировании непрерывные переменные представляются в дискретном виде.
— Для моделей построенных с применением графов, можно воспользоваться многоступенчатым процессом решения, выбранным критерием оптимизации, и составить программы динамической оптимизации процесса при управлении им по определенной стратегии.
Заключение
— Подводе итог, следует отметить, что рассмотрение проблем моделирования химико-технологических процессов, вообще, в отрыве от конкретных особенностей объекта моделирования, было бы полезным для общего развития, но вряд ли позволило бы перекинуть эвристический "мостик" между общим и специфическим подходом "полимерного" характера. Данный курс следует рассматривать именно как такой "мостик".
|
|
|


