 |
Исследование релейной следящей системы с гистерезисом.
|
|
|
|
Рассмотрим теперь случай, когда нелинейная характеристика обладает гистерезисом. Формально она выражается так: 
(21.1)
Нелинейная характеристика принимает всего два значения c и –c. Нетрудно видеть, что фазовая плоскость разбивается на два подмножества точек (x, y), соответствующих этим двум значениям. При этом начало координат не может быть точкой равновесия, поскольку величина y не обращается в нуль. Решение уравнений следящей системы было нами получено на предыдущей лекции в виде (20.4) и мы можем использовать его для построения фазовых траекторий. Положим 
Подставив эти значения в (20.4), получим выражение, из которого можно определить значение постоянной интегрирования 
. (21.2)
Мы, однако, воспользуемся полученным соотношением для другой цели. Попробуем выяснить, не обладает ли фазовая траектория при некоторых начальных условиях свойством центральной симметрии относительно начала координат. Заменив знаки при начальных условиях на противоположные, находим 
(21.3)
Исключая постоянную интегрирования, имеем 
(21.4)
В полученном соотношении все величины кроме ym заданы и если существует ym, удовлетворяющая (21.4), то симметрия фазовой траектории будет доказана и мы получим так называемый предельный цикл или автоколебательный процесс релейной системы с гистерезисом.
Положим для определенности: 
Тогда вместо (21.4) запишем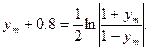 
. (21.5)
На рис.21.1 изображено графическое решение этого уравнения относительно величины ym. Видно, что уравнение имеет по крайней мере два решения, из которых, как мы увидим, только одно может быть реализовано физически.
Рис.21.1. Графическое решение уравнения (21.5).
Решение можно получить с любой точностью, воспользовавшись методом последовательных приближений. В частности, можно использовать легко реализуемый метод - простых итераций. Следует лишь отметить, что условия сходимости этого метода не всегда выполняются, поэтому есть смысл рассмотреть общие условия его сходимости.
|
|
|
Пусть требуется решить уравнение вида 
,(21.6)
где 
- некоторая функция, допускающая существование первой производной. Метод простых итераций строится по формуле 
(21.7)
Теорема
Если в интервале, содержащем корень 
уравнения (21.6),а также все последовательные приближения, получаемые по формуле (21.7), выполняется условие
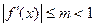, (21.8)
то 
.
Доказательство
По определению 
. Согласно процедуре итераций 
. Следовательно,
Или, согласно известной теореме Лагранжа,
,
где 
Аналогичным путем получаем последовательность оценок
Перемножив оценки, после сокращений находим
.
При выполнении условия (21.8) теоремы получаем
. (21.9)
Переходя в (21.9) к пределу при 
, получаем утверждение теоремы.
Возвращаясь к решению уравнения (21.5), видим из рис.21.1, что метод простых итераций в данном случае не приведет к решению, т.к. не выполняется условие (21.8). В подобных случаях всегда следует «обратить» уравнение, т.е. записать его в виде
. (21.10)
Ограничиваясь, например, пятью значащими цифрами, с помощью (21.10) без труда вычисляем последовательные приближения величины ym: 0.00000
0.66404,
0.89843,
0.93521,
0.93969,
0.94019,
0.94025,
0.94026.
Для построения фазового портрета постоянную интегрирования в выражении (20.4) (см. лекцию 20) можно и не вычислять, т.к. мы располагаем начальными условиями предельного цикла.
Фазовый портрет приведен на рис.21.2. При построении нетрудно подобрать время счета для полного замыкания цикла. В нашем случае это время (период автоколебаний) равно 0.697 с. На рисунке видно и максимальное значение 
, которое при желании можно уточнить.
Рис.21.2. Фазовый портрет релейной
|
|
|
следящей системы с гистерезисом
Получим аналитическое выражение для вычисления периода автоколебаний. Обратимся непосредственно к дифференциальному уравнению (20.2) из предыдущей лекции, которое запишем в виде
.
Общее решение этого уравнения
.
Постоянную интегрирования определяем из начальных условий, полагая при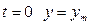 
. Таким образом,
. (21.11)
Обозначив буквой длительность периода автоколебаний, запишем
,
откуда следует
.
Воспользовавшись найденным значением 
, получаем более точное значение периода 
.
Интегрируя (21.11), запишем аналитическое выражение для компоненты x (t) вектора состояния
.
Полагая здесь t = 0, найдем постоянную интегрирования B,после чего запишем искомое выражение
. (21.12)
С помощью формулы (21.12) можно уточнить значение амплитуды автоколебаний. Т.к. максимальное значение x достигается при y =0,то имеет смысл вычислить вначале соответствующий момент времени 
. Согласно (21.11) имеем
.
Следовательно, 
с. Подставив это значение в (21.12), получаем 
- уточненное значение по сравнению с найденным ранее из фазового портрета.
Наконец, при небольшом изменении команды вывода можно получить графики x (t)и y (t) (рис.21.3):
Рис.21.3.График изменения компонент вектора состояния.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 7
|
|
|
