 |
Теоремы А.М. Ляпунова об асимптотической устойчивости и о неустойчивости.
|
|
|
|
Теорема об асимптотической устойчивости
предполагает некоторое усиление требований к производной в силу системы: если для системы уравнений 
(30.9)
существует знакоопределенная функция V (X), производная которойв силу системы (30.9) является также знакоопределенной, но противоположного знака, то решение 
будет асимптотически устойчивым.
Доказательством, не претендующим на математическую строгость, может служить рассуждение ->
Доказательство.
Без ограничения общности будем считать функцию V (X) положительно определенной. Выберем 
и положим 
. Обозначим 
на множестве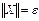 
. Поскольку 
, то из непрерывности функции V (X) следует существование такого числа >0, что 
при 
.
Положим теперь, что начальные условия таковы, что 
. Из условия теоремы производная функции V отрицательна вдоль решения 
. Поэтому функция V не может возрастать вдоль этого решения. Следовательно,
. (28.8)
При этом 
. Если предположить, что это не так, то есть найдется 
, тогда
,
что противоречит (28.8). Остается утверждение 
, что и требовалось. Именно, фазовые траектории будут пересекать линии уровня по направлению к началу координат в любой сколь угодно малой окрестности. Т.к. производная dV /dt обращается в нуль одновременно с функцией Ляпунова, то фазовая траектория пройдет через начало координат, т.е. 
.
Примером асимптотической устойчивости может служить процесс в релейной следящей системе.
Теорема Ляпунова о неустойчивости.
Если для системы уравнений (30.9) существует функция V (X), производная которой в силу системы является знакоопределенной и совпадает по знаку с V (X) в сколь угодно малой окрестности начала координат, то тривиальное решение системы (30.9) неустойчиво.
|
|
|
Для доказательства (на том же уровне, что и в предыдущей теореме) используем тот же геометрический образ из лекции 28. При совпадении знаков функции Ляпунова и ее производной в силу системы угол между вектором градиента и вектором фазовой скорости становится острым. В силу этого существует окрестность начала координат, в которой фазовая траектория с течением времени удаляется от начала. Поэтому не существует сколь угодно малого числа , такого что 
,
в соответствии с определением устойчивого решения.
3.Понятие о системах с перестраиваемыми параметрами. Скользящие режимы в нелинейных системах произвольного порядка.
Начнем с анализа движения консервативной динамической системы второго порядка, описываемой дифференциальным уравнением вида 
.(31.1)
При изучении метода фазового пространства (лекция 19) мы видели, что такому уравнению соответствует особая точка типа центр с эллиптическими фазовыми траекториями вокруг нее. Обратим внимание на ориентацию этих траекторий. Записывая (31.1), как обычно, в форме 
и исключая время, получаем уравнение фазовой траектории в виде 
,
откуда после интегрирования получаем 
или в канонической форме
. (31.2)
Очевидно, при k > 1 эллиптические траектории будут вытянуты вдоль оси y, а при k < 1 – наоборот, т.е. вдоль оси x. Изменяя значения коэффициента k в нужные моменты времени, можно добиться последовательного уменьшения осей эллипсов и в итоге устойчивого положения равновесия (рис.31.1).
Рис.31.1.Преобразование фазового портрета консервативной
системы в портрет, сходящийся к началу.
Переключения в структурной схеме (точнее – скачкообразные изменения величины коэффициента k) выгоднее производить не по времени, а по признаку знака произведения компонент вектора состояния, что и обозначено на рис.31.1. Таким образом, без введения демпфирующих элементов консервативная система превратилась в систему с устойчивым состоянием равновесия.
|
|
|
Следуя этим путем, можно достичь и других эффектов сравнительно простыми средствами. Например, поставим цель осуществить в консервативной системе скользящий режим, рассмотренный нами ранее (см. лекцию 22). Для этого обратимся к результату интегрирования уравнений системы (31.2) и представим, что коэффициент k будет менять не только величину, но и знак. Тогда фазовая плоскость будет заполнена семействами эллиптических и гиперболических траекторий. На рис.31.2 показаны некоторые из этих траекторий, которые последовательно переходят друг в друга на прямой переключения 
.
Рис.31.2. Скользящий режим в консервативной системе.
На этот раз переключение с эллиптической траектории на гиперболическую и обратно должно выполняться по признаку изменения знака величины 
, где m – коэффициент наклона прямой переключения. Скользящий режим наступает, если наклон асимптоты гиперболических траекторий по абсолютной величине превышает наклон прямой переключения. Ниже приведен пакет для рисования фазового портрета 31.2.
Полезно представить себе структурную схему, которая реализует скользящий режим. Поскольку логика переключения строится на изменении знака величины z = y–mx,необходимо выделить в схеме все участвующие здесь координаты, что и выполнено на рис.31.3. Заметим, что указанное выделение составляющих вектора состояния в системах второго порядка астатизма осуществляется естественным путем. Например, в электрогидравлическом приводе эти составляющие реализуются в виде выхода устройства, управляющего производительностью насоса и выхода гидромотора соответственно.
Рис.31.3.Структурная схема с перестройкой под
Скользящий режим.
Рассмотрим, наконец, условия существования скользящего режима в системе, описываемой дифференциальным уравнением произвольного порядка, которое запишем в виде
,
где u – сигнал управления и p - символ дифференцирования.
Введем обозначения для компонент вектора состояния
Подобно предыдущему примеру, для организации скользящего режима образуем линейную комбинацию
,
где без ограничения общности положим cn =1. Кроме того, функция управления 
, принимает два значения
|
|
|
Скользящий режим должен протекать в плоскости y =0 или в соответствии с введенными обозначениями
.
Последнее соотношение можно рассматривать как дифференциальное уравнение скользящего режима.
Можно показать (Емельянов С.В., Уткин В.И. Теория систем с переменной структурой, М.,Наука,1970), что скользящий режим реализуется при выполнении условий
В многомерной системе возникает также вопрос об устойчивости скользящего режима. Достаточным условием устойчивости служит отрицательность вещественных частей корней уравнения
,
кроме одного корня с положительной вещественной частью.
|
|
|
