 |
Дифференцирование обратной функции.
|
|
|
|
Теорема. Пусть y = f (x) непрерывна и монотонна в V (х 0) и дифференцируема в точке х 0, её производная  . Тогда в V (y 0), где
. Тогда в V (y 0), где  определена обратная функция
определена обратная функция  , дифференцируемая в точке y 0 и для её производной в этой точке справедливо:
, дифференцируемая в точке y 0 и для её производной в этой точке справедливо:
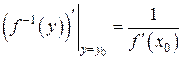 (1)
(1)
или  .
.
Доказательство.
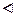 Т.к. f строго монотонна и непрерывна в V (х 0), то в V (y 0) определена обратная функция, также непрерывная и монотонная. Докажем, что обратная функция
Т.к. f строго монотонна и непрерывна в V (х 0), то в V (y 0) определена обратная функция, также непрерывная и монотонная. Докажем, что обратная функция  дифференцируема в точке y 0 и справедливо (1).
дифференцируема в точке y 0 и справедливо (1).
Возьмём  . Значению y 0 аргумента обратной функции придадим приращение
. Значению y 0 аргумента обратной функции придадим приращение  . Тогда обратная функция получит приращение
. Тогда обратная функция получит приращение  .
.
Т.к.  , то
, то  . Действительно, допустим противное:
. Действительно, допустим противное: 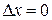 . Тогда
. Тогда  . Т.к.
. Т.к.  - монотонная функция, то отсюда следует, что
- монотонная функция, то отсюда следует, что  . Следовательно,
. Следовательно,  - противоречит условию
- противоречит условию  .
.
Можно записать:
 (2)
(2)
Пусть 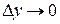 . Тогда в силу непрерывности обратной функции её приращение
. Тогда в силу непрерывности обратной функции её приращение  . По условию
. По условию 
 . Следовательно,
. Следовательно,
существует 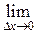 правой части (2):
правой части (2):  . Тогда существует и
. Тогда существует и 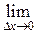 левой части при
левой части при 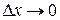 (а, значит, и
(а, значит, и 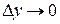 ):
):
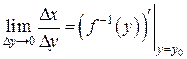
Переходя в равенстве (2) к  , получим (1).
, получим (1). 
Замечание. Если  и
и  в V (х 0)
в V (х 0)  , то
, то  . Если
. Если  , то
, то  .
.
Производные основных элементарных функций.
I. Производная степенной функции y = f (x)= xa,  .
.
 Придадим произвольному значению
Придадим произвольному значению  приращение
приращение  .
.
Тогда  . Разделим на
. Разделим на  :
:
 ,
,
 .
.
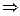
 - существует
- существует  .
. 

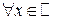 .
.
Частный случай:  ,
, 
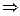
 ,
,
 .
.
II. Производная показательной функции: y = f (x)= ax  ,
, 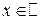 .
.
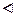 Выберем
Выберем 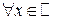 , придадим приращение
, придадим приращение  , тогда
, тогда
 ,
,  ,
,  ,
,
 .
. 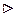

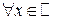 .
.
Частный случай: a = e 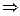
 .
.
III. Производная логарифмической функции 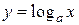
 .
.
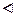
 . Выберем
. Выберем  , придадим приращение
, придадим приращение  , тогда
, тогда
 ,
,
 ,
,
 ,
,
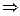
 .
. 
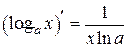
 .
.
Частный случай: a = e 
 .
.
IV. Производные тригонометрических функций.
1)  ,
, 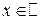 .
.
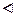 Выберем
Выберем 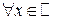 , придадим приращение
, придадим приращение  , тогда
, тогда
 ,
,
 ,
,
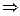
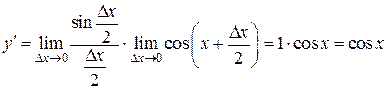 .
. 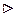
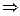

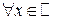 .
.
2)  ,
, 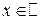 .
.

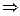
 .
.

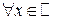 .
.
3) 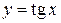 ,
, 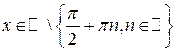 .
.
 .
.

 .
.
4)  ,
,  .
.
 .
.

 .
.
V. Производные обратных тригонометрических функций.
1)  ,
,  .
.
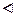
 на
на  непрерывна, строго монотонна (возрастает), дифференцируема:
непрерывна, строго монотонна (возрастает), дифференцируема:  на
на  . Следовательно,
. Следовательно,  по правилу дифференцирования обратной функции
по правилу дифференцирования обратной функции
|
|
|
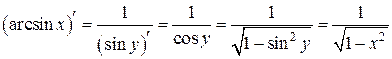
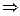
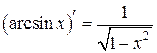
 .
.
Если  , то
, то 
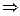
 . Тогда
. Тогда 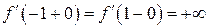

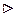
2)  ,
,  .
.
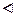

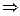

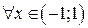

 .
.

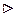
3)  ,
, 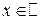 .
.
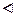
 - обратная функция к
- обратная функция к  на
на  .
.  непрерывна, строго монотонна, дифференцируема и
непрерывна, строго монотонна, дифференцируема и 
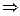

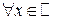
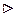

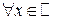 .
.
4) 
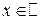 .
.
 .
.

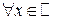 .
.
VI. Производные гиперболических функций.
1)  ,
, 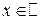 .
.
 ,
, 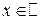
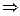

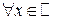 .
.
2)  ,
, 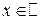 .
.
 Þ
Þ 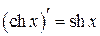
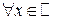 .
.
3)  ,
, 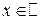 .
.
 , Þ
, Þ 
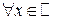 .
.
4)  ,
, 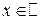 \
\  .
.
 , Þ
, Þ 
 .
.
Производная показательно – степенной функции.
Логарифмическое дифференцирование
Рассмотрим показательно-степенную функцию
 , где
, где  .
.
 .
.
Пример 1. 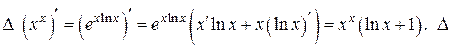
Пусть y = f (x), f (x)>0.

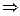
 .
.
Эту формулу используют, когда найти  проще, чем
проще, чем  .
.
Пример 2.  .
.
D  .
.
 Û
Û 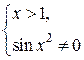
Следовательно,  : x >1 и
: x >1 и 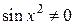


 ,
,
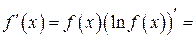
 . D
. D
Производные высших порядков
Пусть функция y = f (x) определена на множестве D и существует  . Тогда на D определена функция
. Тогда на D определена функция  . Если эта функция имеет производную в точке x Î D, то её называют производной второго порядка (или второй производной) функции f (x) в точке x.
. Если эта функция имеет производную в точке x Î D, то её называют производной второго порядка (или второй производной) функции f (x) в точке x.
Обозначается  ,
,  ,
,  ,
, 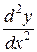 .
.
Таким образом  .
.
Если  существует на D, то она является функцией от х.
существует на D, то она является функцией от х.
Производная от этой функции в некоторой точке x Î D называется производной третьего порядка функции f (x) в точке x.
 .
.
И так далее. Если 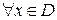
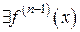 , то на D определена функция
, то на D определена функция  . Производная от этой функции (если она существует) в точке x Î D называется производной n–го порядка функции f (x) в точке x.
. Производная от этой функции (если она существует) в точке x Î D называется производной n–го порядка функции f (x) в точке x.
 .
.
Обозначается:  ,
,  ,
,  ,
,  .
.
Таким образом,  определяется индуктивно. Будем считать
определяется индуктивно. Будем считать 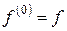 .
.
Заметим, что если существует  в точке х, то в некоторой окрестности
в точке х, то в некоторой окрестности  существует
существует  и все производные более низкого порядка k, k < n.
и все производные более низкого порядка k, k < n.
Если для функции y = f (x) в точке х существует  , то говорят, что функция n раз дифференцируема в этой точке.
, то говорят, что функция n раз дифференцируема в этой точке.
Функция y = f (x) называется n раз непрерывно дифференцируемой, если все её производные до n –го порядка включительно непрерывны в точке х.
Для производных высших порядков справедливы следующие теоремы.
Теорема 1. Если функция y = u (x) имеет производную  , а
, а  , то
, то  имеет производную и справедлива формула
имеет производную и справедлива формула
|
|
|
 .
.
Доказательство.
 1) n =1:
1) n =1:  ;
;
2) n = k:  - верно;
- верно;
n = k +1:  - доказать
- доказать
 .
.
Из 1), 2)  справедливость формулы для любого
справедливость формулы для любого  .
. 
Теорема 2. Пусть  и существуют
и существуют  ,
,  . Тогда существует
. Тогда существует 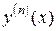 и
и  .
.
Производные высших порядков для некоторых элементарных функций
1) y = f (x)= xa,  .
.
 ,
,  , …
, …
 .
.
Частный случай: 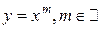
 ,
, 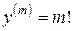

 .
.
2) y = f (x)= ex
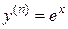
 .
.
3) y = f (x)= ax
 ,
, 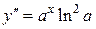 , …
, …
 .
.
4) y =sin x
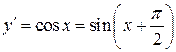 ,
,
 ,
,
 ,
,
 , …
, …
 .
.
5) y =cos x  .
.
6) 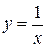
 ,
,  ,
,  ,
,  , …
, …
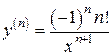
7) y =ln x
 ,
,  , …
, …
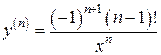
|
|
|


