 |
Основные теоремы дифференциального исчисления
|
|
|
|
Теорема 1 (Ферма, фр., 1601-1665). Пусть функция y = f (x) определена на некотором промежутке < a; b > и в некоторой точке x 0Î< a; b > имеет наименьшее или наибольшее значение. Тогда если функция дифференцируема в точке x 0, то f¢ (x 0)=0.
Доказательство.
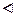Пусть f (x 0) – наибольшее значение функции f (x) на < a; b >. Тогда по определению " x Î< a; b > выполнено f (x)≤ f (x 0).
Если x < x 0, то 
; если x > x 0, то 
.
По условию $ f¢ (x 0), то есть $ f¢ (x 0+0), $ f¢ (x 0 - 0) и f¢ (x 0+0)= f¢ (x 0 - 0)= f¢ (x 0).
Тогда по теореме о предельном переходе в неравенствах 
,
.
Из того, что 
следует, что f¢ (x 0)=0.
Аналогично рассматривается случай, когда f (x 0) – наименьшее значение функции. 
Геометрический смысл. Если функция f, дифференцируемая в точке x 0, имеет в ней наименьшее или наибольшее значение, то в точке (x 0; f (x 0)) касательная к графику функции f (x) параллельна оси О х.
Замечание. Теорема не верна, если x 0 – один из концов отрезка [ a; b ].
Рассмотрим, например, f (x)= x. В точке а – наименьшее значение, в точке b – наибольшее, но 
.
Важно также условие дифференцируемости функции.
Рассмотрим, например, y =| x |. В точке x 0=0- наименьшее значение, но f¢ (x 0)¹0 (f¢ (x 0) не существует).
Теорема 2 (Ролля, фр., 1672-1719). Пусть функция f (x) определена на [ a; b ], причем
1) f (x)ÎC[ a; b ],
2) f (x) дифференцируема на (a; b),
3) f (a)= f (b).
Тогда существует точка с Î(a; b), такая что f¢ (c)=0.
Геометрический смысл. У графика непрерывной на [ a; b ] и дифференцируемой на (a; b) функции f (x), принимающей на концах отрезка [ a; b ] равные значения, существует точка, в которой касательная параллельна оси Ох (таких точек может быть несколько, могут быть и все точки интервала, если m = M (f (x)= с)).
Замечание. Если f (a)= f (b)=0 и выполнены условия теоремы Ролля, то $ с Î(a; b): f¢ (c)=0. То есть между двумя нулями дифференцируемой функции лежит, по крайней мере, один нуль ее производной.
|
|
|
Теорема 3 (Лагранжа, фр., 1736-1813, теорема о конечных приращениях). Пусть функция f (x) определена на [ a; b ], причем
1) f (x)ÎC[ a; b ],
2) f (x) дифференцируема на (a; b).
Тогда существует точка с Î(a; b), такая что 
. (1)
Формула (1) называется формулой Лагранжа. Ее другая форма записи:
f (b) -f (a)= f¢ (c)(b-a). (2)
Геометрический смысл.
, k кас.= f¢ (c),
Þ k кас.= k сек.
На графике существует точка (с; f (c)), касательная в которой параллельна секущей, проходящей через точки (a; f (a)), (b; f (b)).
Пример. На кривой f (x)=4 -x 2 найти точки, в которых касательная параллельна хорде, соединяющей точки (-1;3) и (2;0).
D f (x)=4 -x 2, [ a; b ]=[-1;2], выполнены условия теоремы Лагранжа. Следовательно, существует точка с Î(-1;2), такая что 
.
f¢ (х)= - 2 х Þ 
, - 2 с = - 1, с =0,5. D
Замечание 1. Теорема Ролля является частным случаем теоремы Лагранжа, когда f (a)= f (b).
Замечание 2. Пусть a < b. " с Î(a; b) выполнено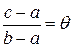 
, 0< q <1 Þ c = a + q (b-a), 0< q <1.
Если a > b, " с Î(a; b) выполнено 
, 0< q <1 Þ 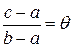Þ c = a + q (b-a), 0< q <1.
Тогда формула (2) примет вид
f (b) -f (a)= f¢ (a + q (b-a))(b-a), 0< q <1. (2¢)
Замечание 3. Пусть функция f удовлетворяет условиям теоремы Лагранжа на [ a; b ]. Произвольному значению x Î[ a; b ] придадим приращение D x, так, что x +D x Î[ a; b ]. Рассмотрим [ x; x +D x ], если D x >0 и [ x +D x; x ], если D x <0. На этом отрезке функция удовлетворяет условиям теоремы Лагранжа. Следовательно,
f (x +D x) -f (x)= f¢ (c) D x = f¢ (x +qD x)D x, 0< q <1,
D f (x)= f¢ (x +qD x)D x. (3)
Формула (3) называется формулой конечных приращений (это тоже формула Лагранжа). Из (3) следует, что если D x конечно, то и D f (x) конечно.
Если сравнить (3) с приближенной формулой D f (x)» f¢ (x)D x, D x ®0, то видно, что при отбрасывании слагаемого a(D x) D x в D f (x) все-таки можно сохранить знак равенства, но для этого надо брать значение производной не в точке х, а в некоторой точке x +qD x, заключенной между х и x +D x. Правда, это значение неизвестно, а установлен только факт его существования. Но это часто используется.
|
|
|
Теорема 4 (Коши, обобщенная теорема о конечных приращениях). Пусть на [ a; b ] определены функции f (x) и g (x), причем
1) f (x), g (x)ÎC[ a; b ],
2) f (x), g (x) дифференцируемы на (a; b),
3) g¢ (x)¹0 " х Î(a; b).
Тогда существует точка с Î(a; b), такая что 
. (4)
Замечание. Теорема Лагранжа является частным случаем теоремы Коши при g (x)= x.
Теоремы Роля, Лагранжа, Коши часто называют теоремами о средних значениях, т. к. в них речь идет о производных при каких-то средних значениях независимой переменной. В теоремах установлен лишь факт существования этих значений. Иногда их можно вычислить.
|
|
|
