Билет. Свойства функций, имеющих предел.

1) Если lim(x стремится к x₀)f(x), то он единственный,

2) Предел константы равен самой константе.

 

Действительно, если f(x)=k, х®х0, то f(x)-k=0=о(1), х®х0 откуда по критерию Þ lim(x стремится к x₀) k=k.

3) Если lim(x стремится к x₀)f(x)=А (конечный), lim(x стремится к x₀) g(x)=B (конечный), то:

- предел суммы (разности) этих функций х®х0 существует и равен сумме (разности) пределов

- предел произведения существует и равен произведению пределов

- предел частного функций существует и равен частному пределов

Билет. Односторонние пределы функции в точке.

Односторонний предел – предел функции в точке слева или справа.

 

Пределом функции f(x) в точке x=a слева называется предел,

вычисляемый в предположении, что x → a, оставаясь все время меньше

значения a. Аналогично, пределом справа называется предел функции f(x)

при x → a, при том, что x > a. Односторонние пределы обозначаются так:

lim f(x) (x стремится к а-0) и lim f(x) (x стремится к а + 0)

Билет. Предел функции на бесконечности.

Предел функции на бесконечности в математическом анализе описывает поведение значения данной функции, когда её аргумент становится бесконечно большим по модулю.

Пусть задана функция у = f(x) с неограниченной сверху областью определения. Число b называется пределом данной функции при х, стремящемся к плюс бесконечности, если для любого числа существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x > M, выполняется неравенство |f(x) – b| < e. Запись этого факта:

Если область определения данной функции неограниченна снизу, то число b называется пределом данной функции при х, стремящемся к минус бесконечности, если для любого числа e < 0 существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x < –M, выполняется неравенство |f(x) – b| < e. Записывается это так (x стр к минус бесконечности вместо плюса):

т

Билет. Теоремы об арифметических свойствах пределов.

 

Теорема 1. (о единственности предела функции). Функция не может иметь более одного предела.

Следствие. Если две функции f (x) и g (x) равны в некоторой окрестности точки , за исключением, может быть, самой точки , то либо они имеют один и тот же предел при , либо обе не имеют предела в этой точке.

Теорема 2. Если функцииf(x) и g(x) имеют пределы в точке , то:

1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.

(2)

2) предел произведения функций равен произведению пределов сомножителей, т.е.

(3)

3) предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.е.

(4)

Замечание. Формулы (2) и (3) справедливы для любого конечного числа функций.

Следствие 1. Предел постоянной равен самой постоянной, т.е.

Следствие 2. Постоянный множитель можно выносить за знак предела, т.е.

 

Теорема 3 (о пределе сложной функции). Если существует конечный предел

а функцияf(u) непрерывна в точке , то

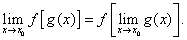
Другими словами, для непрерывных функций символы предела и функции можно поменять местами.

32.Сравнение бесконечно малых функций

Пусть при x → a функции f(x) и g(x) являются бесконечно малыми. Тогда будем пользоваться следующими определениями.

Если 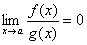, то f(x) называется бесконечно малой высшего порядка, чем g(x) (относительно g(x)).

Если , то функции f(x) и g(x) называются бесконечно малыми одного порядка.

Если , то f(x) называется бесконечно малой k-го порядка относительно g(x).

.Если , то функции f(x) и g(x) называются эквивалентными бесконечно малыми. В этом случае обе функции стремятся к нулю примерно с одинаковой скоростью. Эквивалентные бесконечно малые будем обозначать f ≈ g.

 

 

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: