Глава 2. основы оценки сложных систем

2.1. ОСНОВЫНЫЕ ТИПЫ ШКАЛ ИЗМЕРЕНИЯ

Разработка и эксплуатация информационных, телекоммуникационных, энергетических, транспортных и других сложных систем выявили проблемы, решить которые можно лишь на основе комплексной оценки различных по своей природе факторов, разнородных связей, внешних условий и т. д. В связи с этим в системном анализе выделяют раздел «теория эффективности», связанный с определением качества систем и процессов, их реализующих.

Теория эффективности — научное направление, предметом изучения которого являются вопросы количественной оценки качества характеристик и эффективности функционирования сложных систем.

В общем случае оценка сложных систем может проводиться для разных целей. Во-первых, для оптимизации — выбора наилучшего алгоритма из нескольких, реализующих один закон функционирования системы. Во-вторых, для идентификации — определения системы, качество которой наиболее соответствует реальному объекту в заданных условиях. В-третьих, для принятия решений по управлению системой. Перечень частных целей и задач, требующих оценки систем, можно продолжить. Общим во всех подобных задачах является подход, основанный на том, что понятия «оценка» и «оценивание» рассматриваются раздельно и оценивание проводится в несколько этапов. Под оценкой понимают результат, получаемый в ходе процесса, который определен как оценивание. Принято считать, что с термином «оценка» сопоставляется понятие «истинность», а с термином «оценивание» — «правильность». Другими словами, истинная оценка может быть получена только при правильном процессе оценивания. Это положение определяет место теории эффективности в задачах системного анализа.

Выделяют четыре этапа оценивания сложных систем.

Этап 1. Определение цели оценивания. В системном анализе выделяют два типа целей. Качественной называют цель, достижение которой выражается в номинальной шкале или в шкале порядка. Количественной называют цель, достижение которой выражается в количественных шкалах. Определение цели должно осуществляться относительно системы, в которой рассматриваемая система является элементом (подсистемой).

Этап 2. Измерение свойств систем, признанных существенными для целей оценивания. Для этого выбираются соответствующие шкалы измерений свойств и всем исследуемым свойствам систем присваивается определенное значение на этих шкалах.

Этап 3. Обоснование предпочтений критериев качества и критериев эффективности функционирования систем на основе измеренных на выбранных шкалах свойств.

Этап 4. Собственно оценивание. Все исследуемые системы, рассматриваемые как альтернативы, сравниваются по сформулированным критериям и в зависимости от целей оценивания ранжируются, выбираются, оптимизируются и т.д.

2.1.1. ПОНЯТИЕ ШКАЛЫ

В основе оценки лежит процесс сопоставления значений качественных или количественных характеристик исследуемой системы значениям соответствующих шкал. Исследование характеристик привело к выводу о том, что все возможные шкалы принадлежат к одному из нескольких типов, определяемых перечнем допустимых операций на этих шкалах.

Формально шкалой называется кортеж из трех элементов < Х, j, Y>, где Х реальный объект, Y шкала, j гомоморфное отображение Х на Y.

В современной теории измерений определено:

Х = { x ₁, x ₂, …, x _i, …, x _n, R _x } эмпирическая система с отношением, включающая множество свойств x _j, на которых в соответствии с целями измерения задано некоторое отношение R _x. В процессе измерения необходимо каждому свойству x _i Î Х поставить в соответствие признак или число, его характеризующее. Если, например, целью измерения является выбор, то элементы x _i, рассматриваются как альтернативы, а отношение й„должно позволять сравнивать эти альтернативы;

Y = {j(x₁), …,j(x_n), R _x} знаковая система с отношением, являющаяся отображением эмпирической системы в виде некоторой образной или числовой системы, соответствующей измеряемой эмпирической системе;

j Î Ф - гомоморфное отображение Х на Y, устанавливающее соответствие между Х и Y так, что {j(x₁), …,j(x_n)} Î R _y только тогда, когда {x₁, …,x_n} Î R _x.

Тип шкалы определяется по Ф = {j₁, …, j_m}, множеству допустимых преобразований x_i ® y_i.

В соответствии с приведенными определениями, охватывающими как количественные, так и качественные шкалы, измерение эмпирической системы Х с отношением R _x состоит в определении знаковой системы Y с отношением R _y, соответствующей измеряемой системе. Предпочтения R _x на множестве Х ´ Х в результате измерения переводятся в знаковые (в том числе и количественные) соотношения R _y на множестве Y ´ Y.

2.1.2. шкалы номинального Типа

Самой слабой качественной шкалой является номинальная (шкала наименований, классификационная шкала), по которой объектам х. или их неразличимым группам дается некоторый!признак. Основным свойством этих шкал является сохранение неизменными отношений равенства между элементами эмпирической системы в эквивалентных шкалах.

Шкалы номинального типа задаются множеством взаимно однозначных допустимых преобразований шкальных значений.

Название «номинальный» объясняется тем, что такой признак дает лишь ничем не связанные имена объектам. Эти значения для разных объектов либо совпадают, либо различаются; никакие более тонкие соотношения между значениями не зафиксированы. Шкалы номинального типа допускают только различение объектов на основе проверки выполнения отношения равенства на множестве этих элементов.

Номинальный тип шкал соответствует простейшему виду измерений, при котором шкальные значения используются лишь как имена объектов, поэтому шкалы номинального типа часто называют также шкалами наименований.

Примерами измерений в номинальном типе шкал могут служить номера автомашин, телефонов, коды городов, лиц, объектов и т. п. Единственная цель таких измерений выявление различий между объектами разных классов. Если каждый класс состоит из одного объекта, шкала наименований используется для различения объектов.

На рис. 2.1 изображено измерение в номинальной шкале объектов, представляющих три множества элементов А, В, С. Здесь эмпирическую систему представляют четыре элемента: a Î А, b Î В, { с, d } Î С, принадлежащих соответствующим множествам. Знаковая система представлена цифровой шкалой наименований, включающей элементы 1, 2,..., n и сохраняющей отношение равенства. Гомоморфное отображение j ставит в соответствие каждому элементу из эмпирической системы определенный элемент знаковой системы.

Следует обратить внимание на две особенности номинальных шкал. 1

Во-первых, элементам с и d поставлено в соответствие одно и то же значение шкалы измерения (см. рис. 2.1). Это означает, что при измерении эти элементы не различаются.

Во-вторых, при измерении в шкале наименований символы 1, 2, 3,..., n, используемые в качестве шкальных значений, являются не числами, а цифрами, служащими лишь для обозначения и различия объектов. Так, цифра 2 не является в два раза или на единицу больше цифры 1 в отличие от чисел 2 и 1.

Всякая обработка результатов измерения в номинальной шкале должна учитывать данные особенности. В противном случае могут быть сделаны ошибочные выводы по оценке систем, не соответствующие действительности.

2.1.3. ШКАЛЫ ПОРЯДКА

Шкала называется ранговой (шкала порядка), если множество Ф состоит из всех монотонно возрастающих допустимых преобразований шкальных значений.

Монотонно возрастающим называется такое преобразование j(х), которое удовлетворяет условию: если x₁>х₂, то и j(х₁)> j(х₂) для любых шкальных значений x₁>x₂ из области определения j(х). Порядковый тип шкал допускает не только различие объектов, как номинальный тип, но и используется для упорядочения объектов по измеряемым свойствам. Измерение в шкале порядка может применяться, например, в следующих ситуациях:

• необходимо упорядочить объекты во времени или пространстве. Это ситуация, когда интересуются не сравнением степени выраженности какого-либо их качества, а лишь взаимным пространственным или временным расположением этих объектов;

• нужно упорядочить объекты в соответствии с каким-либо качеством, но при этом не требуется производить его точное измерение;

• какое-либо качество в принципе измеримо, но в настоящий момент не может быть измерено по причинам практического или теоретического характера.

 

Примером шкалы порядка может служить шкала твердости минералов, предложенная в 1811 г. немецким ученым Ф. Моосом и до сих пор распространенная в полевой геологической работе. Другими примерами шкал порядка могут служить шкалы силы ветра, силы землетрясения, сортности товаров в торговле, различные социологические шкалы и т.п.

Любая шкала, полученная из шкалы порядка S с помощью произвольного монотонно возрастающего преобразования шкальных значений, будет также точной шкалой порядка для исходной эмпирической системы с отношениями.

Несколько более «сильными», чем порядковые шкалы, являются шкалы гиперпорядка. Допустимыми для этих шкал являются гипермонотонные преобразования, т.е. преобразования j(x), такие, что для любых x₁, x₂, x₃ и x₄

только когда x₁, x₂, x₃ и x₄ принадлежат области определения j(x) и x₁- x₂< x₃ - x₄.

При измерении в шкалах гиперпорядка сохраняется упорядочение разностей численных оценок.

2.1.4. ШКАЛЫ ИНТЕРВАЛОВ

Одним из наиболее важных типов шкал является тип интервалов. Тип шкал интервалов содержит шкалы, единственные с точностью до множества положительных линейных допустимых преобразований вида j(x) = ах + b, где х Î Y - шкальные значения из области определения Y; a >0; b - любое значение.

Основным свойством этих шкал является сохранение неизменными отношений интервалов в эквивалентных шкалах:

Отсюда и происходит название данного типа шкал. Примером шкал интервалов могут служить шкалы температур. Переход от одной шкалы к эквивалентной, например от шкалы Цельсия к шкале Фаренгейта, задается линейным преобразованием шкальных значений: t ^o F = 1,8 t ^o C + 32.

Другим примером измерения в интервальной шкале может служить признак «дата совершения события», поскольку для измерения времени в конкретной шкале необходимо фиксировать масштаб и начало отсчета. Григорианский и мусульманский календари две конкретизации шкал интервалов.

Таким образом, при переходе к эквивалентным шкалам с помощью линейных преобразований в шкалах интервалов происходит изменение как начала отсчета (параметр b), так и масштаба измерений (параметр а).

Шкалы интервалов так же, как номинальная и порядковая, сохраняют различие и упорядочение измеряемых объектов. Однако кроме этого они сохраняют и отношение расстояний между парами объектов. Запись

означает, что расстояние между x ₁ и x ₂в K раз больше расстояния между x ₃и x ₄ и в любой эквивалентной шкале это значение (отношение разностей численных оценок) сохранится. При этом отношения самих оценок не сохраняются.

В социологических исследованиях в шкалах интервалов обычно измеряют временные и пространственные характеристики объектов. Например, даты событий, стаж, возраст, время выполнения заданий, разницу в отметках на графической шкале и т.д. Однако прямое отождествление замеренных переменных с изучаемым свойством не столь просто.

В качестве другого примера рассмотрим испытание умственных способностей, при котором измеряется время, требуемое для решения какой-нибудь задачи. Хотя физическое время измеряется в шкале интервалов, время, используемое как мера умственных способностей, принадлежит шкале порядка. Для того чтобы построить более совершенную шкалу, необходимо исследовать более богатую структуру этого свойства.

Типичная ошибка: свойства, измеряемые в шкале интервалов, принимаются в качестве показателей для других свойств, монотонно связанных с данными.

Применяемые для измерения связанных свойств исходные шкалы интервалов становятся всего лишь шкалами порядка. Игнорирование этого факта часто приводит к неверным результатам.

2.1.6. ШКАЛЫ ОТНОШЕНИЙ

Шкалой отношений (подобия) называется шкала, если Ф состоит из преобразований подобиями j(х) = ах, а > 0, где x Î Y — шкальные значения из области определения Y; а - действительные числа.

Нетрудно убедиться, что в шкалах отношений остаются неизменными отношения численных оценок объектов. Действительно, пусть в одной шкале объектам a₁ и а₂ соответствуют шкальные значения x₁ и x₂,а в другой j(x₁)=ax₁ и j(x₂)=ax₂, где а > 0 — произвольное действительное число. Тогда имеем:

Данное соотношение объясняет название шкал отношений. Примерами измерений в шкалах отношений являются измерения массы и длины объектов. Известно, что при установлении массы используется большое разнообразие численных оценок. Так, производя измерение в килограммах, получаем одно численное значение, при измерении в фунтах — другое и т.д. Однако можно заметить, что в какой бы системе единиц ни производилось измерение массы, отношение масс любых объектов одинаково и при переходе от одной числовой системы к другой, эквивалентной, не меняется. Этим же свойством обладает и измерение расстояний и длин предметов.

Как видно из рассмотренных примеров, шкалы отношений отражают отношения свойств, т.е. во сколько раз свойство одного объекта превосходит это же свойство другого объекта.

Шкалы отношений образуют подмножество шкал интервалов фиксированием нулевого значения параметра b:b = 0. Такая фиксация означает задание нулевой точки начала отсчета шкальных значений для всех шкал отношений. Переход от одной шкалы отношений к другой, эквивалентной ей шкале осуществляется с помощью преобразований подобия (растяжения), т.е. изменением масштаба измерений. Шкалы отношений, являясь частным случаем шкал интервалов, при выборе нулевой точки отсчета сохраняют не только отношения свойств объектов, но и отношения расстояний между парами объектов.

2.1.6 ШКАЛЫ РАЗНОСТЕЙ

Шкалы разностей определяются как шкалы, единственные с точностью до преобразований сдвига j(x)=x+b, где x Î Y - шкальные значения из области определения Y; b - действительные числа. Это означает, что при переходе от одной числовой системы к другой меняется лишь начало отсчета.

Шкалы разностей применяются в тех случаях, когда необходимо измерить, насколько один объект превосходит по определенному свойству другой объект. В шкалах разностей неизменными остаются разности численных оценок свойств. Действительно, если x₁ и x₂ - оценки объектов a₁ и a₂ в одной шкале, а j(x₁)=x₁+b и j(x₂)=x₂+b - в другой шкале, то имеем:

Примерами измерений в шкалах разностей могут служить измерения прироста продукции предприятий (в абсолютных единицах) в текущем году по сравнению с прошлым, увеличение численности учреждений, количество приобретенной техники за год и т. д.

Другим примером измерения в шкале разностей является летоисчисление (в годах). Переход от одного летоисчисления к другому осуществляется изменением начала отсчета,

Как и шкалы отношений, шкалы разностей являются частным случаем шкал интервалов, получаемых фиксированием параметра а: (а = 1), т.е. выбором единицы масштаба измерений. Точка отсчета в шкалах разностей может быть произвольной.

 

Шкалы разностей, как и шкалы интервалов, сохраняют отношения интервалов между оценками пар объектов, но, в отличие от шкалы отношений, не сохраняют отношения оценок свойств объектов.

2.1.7. АБСОЛЮТНЫЕ ШКАЛЫ

Абсолютными называют шкалы, в которых единственными допустимыми преобразованиями Ф являются тождественные преобразования: j(x)= { e }, где e(x)=x.

Это означает, что существует только одно отображение эмпирических объектов в числовую систему. Отсюда и название шкалы, так как для нее единственность измерения понимается в буквальном абсолютном смысле.

Абсолютные шкалы применяются, например, для измерения количества объектов, предметов, событий, решений и т.п. В качестве шкальных значений при измерении количества объектов используются натуральные числа, когда объекты представлены целыми единицами, и действительные числа, если кроме целых единиц присутствуют и части объектов.

Абсолютные шкалы являются частным случаем всех ранее рассмотренных типов шкал, поэтому сохраняют любые соотношения между числами оценками измеряемых свойств объектов: различие, порядок, отношение интервалов, отношение и разность значений и т.д.

Кроме указанных существуют промежуточные типы шкал, такие, например, как степенная шкала j(x)=ax^b; а > 0, b> 0, а ¹1, b ¹1, и ее разновидность логарифмическая шкала j(x)=x^b; b > 0, b ¹1.

Не останавливаясь подробно на промежуточных вариантах, изобразим для наглядности соотношения между основными типами шкал в виде иерархической структуры основных шкал (рис. 2.2). Здесь стрелки указывают включение совокупностей допустимых преобразований более «сильных» в менее «сильные» типы шкал. При этом шкала тем «сильнее», чем меньше свободы в выборе j(x).

Некоторые шкалы являются изоморфными, т.е. равносильными. Например, равносильны шкала интервалов и степенная шкала. Логарифмическая шкала равносильна шкале разностей и шкале отношений.

 

2.2. ОБРАБОТКА ХАРАКТЕРИСТИК, ИЗМЕРЕННЫХ В РАЗНЫХ ШКАЛАХ

При проведении измерений необходимо отделять существенно несравнимые альтернативы от несравнимых альтернатив, допускающих косвенную сравнительную оценку.

Так, например, если эксперт считает несравнимыми альтернативы y₁ и y₂, но время считает альтернативу y₁ более предпочтительной, а альтернативу у₂ менее предпочтительной, чем y₃,то можно с определенными оговорками считать y₁, более предпочтительной, чем у₂. Отношение R_y при наличии несравнимых альтернатив является отношением частичного порядка. В этом случае вводится понятие квазишкалы.

Особенностью измерения и оценивания качества сложных систем является то, что для одной системы по разным частным показателям качества могут применяться любые из типов шкал от самых слабых до самых сильных. При этом для получения надежного значения показателя может проводиться несколько измерений. Кроме того, обобщенный показатель системы может представлять собой некую осредненную величину однородных частных показателей.

При измерении и оценке физических величин обычно трудностей не возникает, так как перечисленные величины измеряются в абсолютной шкале. Измерение, например, ряда антропометрических характеристик осуществляется в шкале отношений. Более сложной является оценка в качественных шкалах. Однако отдельные показатели в процессе системного анализа уточняются, и, как следствие, появляется возможность от измерения и оценки в качественных шкалах перейти к оценке в количественных шкалах.

В любом случае при работе с величинами, измеренными в разных шкалах, необходимо соблюдать определенные правила, которые не всегда очевидны. Иначе неизбежны грубые просчеты и промахи при оценке систем. Проиллюстрируем широко распространенную ошибку при использовании балльной оценки. Пусть для экспертизы представлены две системы А и Б, оцениваемые по свойствам y₁, y₂, у₃, у₄. Качество каждой системы оценивается как среднеарифметическое по пятибалльной системе, но оценка в баллах является вследствие округления не совсем точной. Так, например, свойства, имеющие фактический уровень 2,6 и 3,4 балла, получат одинаковую оценку 3 балла. Результаты экспертизы приведены в табл. 2.1.

По фактическому качеству лучшей является система А, а по результатам экспертизы лучшей признают систему Б. Таким образом, способы измерения и обработки их результатов оказывают существенное влияние на результаты.

 

Таблица 2.1 Пример балльной оценки свойств систем

Свойство системы	Система А	Система Б
истинная	в баллах	истинная	в баллах
y1	4,4		3,6
y2	3,3		3,7
y3	2,4		2,6
y4	4,4		2,6
Суммарная оценка	14,5		12,5

Избежать ошибок можно, используя результаты, полученные в теории шкалирования, они определяют правила и перечень допустимых операций осреднения характеристик. Остановимся подробнее на правилах осреднения.

Проводить осреднение допускается только для однородных характеристик, измеренных в одной шкале. Это означает, например, что не имеет физического смысла вычисление среднего значения скорости для мобильного абонентского пункта, если слагаемыми являются скорость передачи данных и скорость перемещения этого объекта. Иными словами, усредняются только такие значения y_i, i= 1,..., п, которые представляют собой или оценки различных измерений одной и той же характеристики, или оценки нескольких различных однородных характеристик.

Каждое значение показателя y_i может иметь для исследователя различную ценность, которую учитывают с помощью коэффициентов значимости с_i, причем .

Для получения осредненного значения показателя наиболее часто применяют основные формулы осреднения (табл. 2.2).

 

Таблица 2.2 Основные формулы осреднения показателей

Наименование	Формула
Средневзвешенное арифметическое (СВА)
Среднеарифметическое (СА), частный случай СВА при равнозначности измерений (c i =1/ n)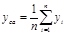
Среднеквадратичное (СК)
Средневзвешенное геометрическое (СВГм)
Среднегеометрическое (СГм), частный случай СВГм при c i =1/ n
Средневзвешенное гармоническое (СВГр)
Среднегармоническое (СГр)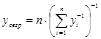

Простая и взвешенные средние величины различаются не только по величине (не всегда), по способу вычисления, но и по своей роли в решении задач системного анализа. При этом средневзвешенные величины используются для сравнения систем с учетом вклада различных факторов в осредненную оценку. Рассмотрим, например, среднее количество информации, получаемой из сети Интернет организацией, пользующейся услугами различных прикладных служб. Если эта средняя величина входит в систему показателей себестоимости, протоколов работы, типов используемых линий, то следует применять взвешенное среднее, так как произведение невзвешенного среднего на общую пропускную способность линий не даст количества полученной информации, поскольку служба электронной почты используется, например, значительно реже, чем WWW, и, следовательно, вносит меньший вклад в общее количество получаемой информации. Если же необходимо изучить связь количества получаемой информации с днем недели, то следует применять простое среднее количество информации за сутки, полностью абстрагируясь от различий между типами служб.

Среднеарифметическое используется в случаях, когда важно сравнить абсолютные значения какой-либо характеристики нескольких систем. Например, скорость вывода на печать текстов (лист/мин) для различных печатающих устройств.

Если при замене индивидуальных значений показателя на среднюю величину требуется сохранить неизменной сумму квадратов исходных величин (измерение вариации характеристики в совокупности), то в качестве средней следует использовать среднеквадратичное. Например, при определении местоположения источника радиоизлучения в радиоразведке вычисляется среднеквадратичное отклонение нескольких измерений.

Среднегеометрическое, в свою очередь, используется для определения относительной разности отдельных значений при необходимости сохранения произведения индивидуальных величин тогда, когда среднее значение качественно одинаково удалено от максимального и минимального значений, т.е. когда важны не абсолютные значения, а относительный разброс характеристик. Например, если максимальная производительность процессора на операциях с данными целочисленного типа составляет для сжатия текстового файла миллион условных единиц, а для ежатия изображений графических объектов сто, то какую величину считать средней? Среднеарифметическое (500 000) качественно однородно с максимальным и резко отлично от минимального. Среднегеометрическое по логике дает верный ответ: 10 000. Не миллион, и не сотня, а нечто среднее. В статистике среднегеометрическое находит применение при определении средних темпов роста.

Среднегармоническое используется, если необходимо, чтобы неизменной оставалась сумма величин, обратных индивидуальным значениям характеристик. Пусть, например, в режиме обмена данными средняя скорость передачи данных по прямому каналу составляет 64 Кбайт/с, а средняя скорость по обратному каналу 2,4 Кбайт/с. Какова средняя скорость обмена данными? При замене индивидуальных значений скорости y₁ = 64 и у₂ = 2,4 на среднюю величину необходимо, чтобы неизменной величиной осталось время передачи в обе стороны, иначе средняя скорость может оказаться любой. Таким образом, у_ср = 2(1/64+1/2,4)^-1 @ - 4,8 Кбайт/с.

Приведенные примеры показывают, что в каждом конкретном случае требуется четкое определение допустимых условий применения средних величин.

Соотношение между разными типами средних величин определяется правилом мажорантности средних СГр < СГм < СА < СК.

Использование необоснованных способов определения средних величин может привести к искусственному завышению или занижению осредненного значения показателя качества системы. В качестве упражнения обучаемым предлагается определить свой средний балл за прошедшую сессию на основе перечисленных средних величин.

Сводные данные по характеристикам разных шкал и перечень допустимых операций осреднения характеристик приведены в табл. 2.3, откуда следует, что для величин, измеренных в номинальной шкале, никаких осреднений производить не допускается.

Среднеарифметическое применимо для величин, измеренных в шкалах интервалов, разностей, отношений и абсолютной, но недопустимо для шкалы порядка.

Более устойчивой оценкой среднего является медиана (50-процентный квантиль), которая рекомендуется как основной показатель для шкал порядка, интервалов, разностей, отношений и абсолютной. Математическое ожидание допустимо для шкал интервалов, разностей, отношений и абсолютных, но не столь устойчиво, как медиана. Применение математического ожидания для величин, измеренных в шкале порядка, является некорректным. Среднегеометрическое является единственно допустимым средним для степенных и логарифмических шкал, а также одним из допустимых для шкалы отношений. Для шкалы отношений допустимы также средневзвешенное арифметическое, среднегармоническое и среднеквадратичное.

Вопрос о применении средних в настоящее время исследован достаточно полно. Этого нельзя сказать о средневзвешенных. Однако для наиболее часто применяемого средневзвешенного арифметического доказан следующий факт. Средневзвешенное арифметическое, часто применяемое как обобщенный линейный критерий (аддитивная свертка при сведении векторной задачи к скалярной, при осреднении показателей и др.), допустимо использовать тогда и только тогда, когда значения частных показателей можно представить мультипликативным метризованным отношением линейного порядка или, другими словами, когда они измерены в шкале отношений. Доказано, что задача линейного программирования корректна, если коэффициенты ее целевой функции и ограничений измерены в шкале отношений.

Будущее развития теории шкалирования и ее применения для нужд математического обеспечения ИС связаны с дальнейшим развитием понятия измерения. Наиболее перспективным представляется расширение понимания шкалы путем привлечения понятий нечеткой и лингвистических переменных, используемых в теории нечетких множеств. Обобщение понятия характеристической функции путем перехода к понятию функции принадлежности m_nÎ[0,1], используемой в этой теории, создает базу для введения более тонкой структуры измерения качественных характеристик и учета неопределенностей, свойственных сложным системам, на основе понятия нечеткой шкалы.

Например, пусть рассматриваемое нечеткое множество возраст людей. Нечеткими переменными (шкальными значениями), означающими возраст, являются лингвистические переменные «молодой», «средний», «старый» с приписанными им функциями принадлежности, которые можно определить так, как показано на рис. 2.3. При этом 20-летний человек относится к нечеткому подмножеству возраста «молодой» с функцией принадлежности m_мол = 0,8, и он же с функцией принадлежности m_ср = 0,1 относится к нечеткому подмножеству возраста «средний».

 

2.3. ПОКАЗАТЕЛИ И КРИТЕРИИ ОЦЕНКИ СИСТЕМ

Искусственные системы создаются, как правило, для реализации одной или ряда операций. Требуемый и реально достигаемый системой результаты могут различаться. Это зависит от условий протекания операции, качества системы, реализующей операцию, и способов достижения требуемых результатов. Поэтому при оценке систем принято различать качество систем и эффективность реализуемых системами процессов.

Эффективность относят не к самой системе, а к выполняемой ею операции. Эффективность, как группа свойств, представляет только качество функционирования системы соответствие требуемого и достигаемого результата.

2.3.1. ВИДЫ КРИТЕРИЕВ КАЧЕСТВА

Соотношение понятий качества и эффективности представлено в табл. 2.4. Для рассмотрения утверждений, приведенных в табл. 2.4, введем ряд понятий.

Таблица 2.4

Соотношение понятий качества и эффективности систем

Параметр	Качество	Эффективность
Определение	Свойство или совокупность системы, обусловливающих ее пригодность (соответствие) для использования по назначению	Комплексное операционное свойство (качество) процесса функционирования системы, характеризующее его приспособленность к достижению цели операции (выполнению задачи системы)
Область применения'	Объекты любой природы, в том числе элементы систем	Только целенаправленные операции, проводимые системой
Основная характеристика	Совокупность атрибутивных свойств системы, существенных для ее использования по назначению	Степень соответствия результатов операции ее цели
Фактор структурного анализа	Строение системы (состав той структура организация)	Алгоритм функционирования, качество системы, реализующей алгоритм, воздействия внешней среды
Размерность	Показатель качества — вектор показателей существенных свойств	Показатели результативности, ресурсоемкости, оперативности по исходу операции и по качеству «алгоритма», обеспечивающего получение результатов
Способ оценивания -	Критерии пригодности, оптимальности, превосходства	Критерии пригодности или оптимальности, определяемые в зависимости от типа проводимой операции (детерминированная, вероятностная или неопределенная)

Каждое i -е качество j -й системы, i = 1,..., n; j = 1,..., m, может быть описано с помощью некоторой выходной переменной у^j_i, отображающей определенное существенное свойство системы, значение которой характеризует меру (интенсивность) этого качества. Эту меру назовем показателем свойства или частным показателем качества системы. Показатель у ^j _i, может принимать значения из множества (области) допустимых значений .

Назовем обобщенным показателем качества j-й системы вектор 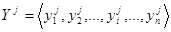, компоненты которого суть показатели его отдельных свойств. Размерность этого вектора определяется числом существенных свойств системы. Обратим внимание на то, что показатель качества именно вектор, а не простое множество частных показателей, поскольку между отдельными свойствами могут существовать связи, которые в рамках теории множеств описать весьма сложно.

Частные показатели имеют различную физическую природу и в соответствии с этим различную размерность. Поэтому при образовании обобщенного показателя качества следует оперировать не с «натуральными» показателями, а с их нормированными значениями, обеспечивающими приведение показателей к одному масштабу, что необходимо для их сопоставления.

Задача нормировки решается, как правило, введением относительных безразмерных показателей, представляющих собой отношение «натурального» частного показателя к некоторой нормирующей величине, измеряемой в тех же единицах, что и сам показатель

где у ⁰_i — некоторое «идеальное» значение i- го показателя.

Выбор нормирующего делителя для перевода частных показателей в безразмерную форму в значительной мере носит субъективный характер и должен обосновываться в каждом конкретном случае.

Возможны несколько подходов к выбору нормирующего делителя.

Во-первых, нормирующий делитель у ⁰_i можно задавать с помощью ЛПР, и это предполагает, что значение у ⁰_i является образцовым.

Во-вторых, можно принять, что нормирующий делитель у ⁰_i=max у ^j_i.

В-третьих, в качестве нормирующего делителя может быть выбрана разность между максимальными и минимальными допустимыми значениями частного показателя.

Требуемое качество системы задается правилами (условиями), которым должны удовлетворять показатели существенных свойств, а проверка их выполнения называется оцениванием качества системы. Таким образом, критерий качества это показатель существенных свойств системы и правило его оценивания.

Назовем идеальной системой Y ^* гипотетическую модель исследуемой системы, идеально соответствующую всем критериям качества, вектор, являющийся показателем качества идеальной

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: