 |
Эквивалентные системы векторов. Свойство линейно независимых эквивалентных систем векторов.
|
|
|
|
Вектор — понятие, определяемое в разных разделах математики различно.
Линейное пространство — это множество элементов, называемых векторами, над которыми определённым образом определены операции сложения и умножения на число. В любом линейном пространстве можно выделить особую систему векторов, называемых базисом линейного пространства. Количество векторов в базисе равно размерности пространства.
Системы векторов называются эквивалентными, если векторы одной системы линейно выражаются через систему других векторов и наоборот
Теорема. Если система векторов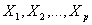 
линейно-зависима, то она эквивалентна системе 
Доказательстово. Действительно, пусть 
одновременно неравные нулю числа такие, что 
. Предположим, что 
S 
0, разделим эту сумму на S, получим: 
или
, где 
.
Заменим систему векторов 
эквивалентной системой 
с помощью следующего элементарного преобразования:
при 
и 
. Тогда вектор 
. Поменяв местами векторы 
и 
получим систему вида . Что и требовалось доказать.
Следствие. Произвольную систему векторов элементарными преобразованиями можно привести к системе вида 
, где
линейно независимая система векторов.
Число 
будем называть рангом системы векторов , а систему
– базисом системы векторов .
Отметим, что ранг системы векторов не зависит от конкретной цепочки элементарных преобразований.
Система векторов называется линейно независимой, если из 
следует, что 
Пример 2. Система векторов 
из примера 1 линейно независима.
Действительно из 
следует, что 
.
Базис конечной системы векторов. Ранг конечной системы векторов, корректность определения.
Базис (др. греч βασις, основа) — множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества — базисных векторов.
|
|
|
Базисом системы векторов A1, A2,..., An называется такая подсистема B1, B2,...,Br (каждый из векторов B1,B2,...,Br является одним из векторов A1, A2,..., An), которая удовлетворяет следующим условиям:
1. B1,B2,...,Br линейно независимая система векторов;
2. любой вектор Aj системы A1, A2,..., An линейно выражается через векторы B1,B2,...,Br
r — число векторов входящих в базис.
Теорема. Любые два базиса конечной системы векторов S содержат одно и то же число векторов.
Доказательство. Пусть 
и 
– базисы системы векторов S. Предположим, что m > k. Так как любой вектор системы векторов можно представить в виде линейной комбинации системы векторов 
, то согласно свойству 5 система векторов линейно зависимая (противоречие). Значит, неверно, что m > k. Аналогично показывается, что k m. Следовательно, m = k.
Определение. Рангом системы векторов S называется число векторов в любом ее базисе и обозначается rang(S).
Следующие преобразования системы векторов называются элементарными:
α) исключение (добавление) нулевого вектора;
β) умножение любого вектора системы на скаляр 
, λ ≠ 0;
γ) прибавление к любому вектору системы любого другого вектора этой системы векторов, умноженного на скаляр , λ ≠ 0.
Если система векторов 
получена из системы векторов посредством элементарных преобразований α), β), γ), то rang() = rang().
Теорема. Если rang() = rang(), то вектор можно представить в виде линейной комбинации системы векторов .
Доказательство. Пусть rang() = S и базис этой системы. Так как, rang() = rang(), то система векторов – линейно зависимая. Согласно свойству 4 линейной зависимости и независимости векторов, Так как , то Следовательно, существуют такие что
|
|
|
|
|
|
