Элементарные преобразования систем векторов. Ступенчатая система векторов.

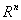Пусть – система векторов m из . Основными элементарными преобразованиями системы векторов являются

1. - добавление к одному из векторов (вектору ) линейной комбинации остальных.

2. - умножение одного из векторов (вектора ) на число не равное нулю.

3. перестановка двух векторов ( ) местами. Системы векторов , будем называть эквивалентными (обозначение ), если существует цепочка элементарных преобразований переводящая первую систему во вторую.

Отметим свойства введенного понятия эквивалентности векторов

(рефлексивность)

Из 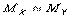следует, что (симметричность)

Если 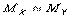и , то (транзитивность) Теорема. Если система векторов линейно независима, а 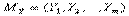ей эквивалентна, то система – линейно независима. Доказательство. Очевидно, что теорему достаточно доказать для системы полученной из с помощью одного элементарного преобразования.. Предположим что система векторов линейно независима. Тогда из вытекает, что . Пусть система получена из с помощью одного элементарного преобразования. Очевидно, что перестановка векторов или умножение одного из векторов на число не равное нулю не меняет линейной независимости системы векторов. Допустим теперь, что система векторов 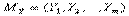получена из системы прибавлением к вектору линейной комбинации остальных, 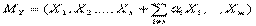. Нужно установить, что (1) вытекает что Поскольку , то из (1) получаем . (2)

Т.к. система – линейно независима, то из (2) следует, что для всех .

Отсюда получаем . Что и требовалось доказать.

 

 

54-56

57. Матрицы. сложение матриц умножение матрицы на скляр матрицы как векторное пространство его размерность.

Матрицей называется прямоугольная таблица чисел, состоящая из m одинаковой длины строк или n одинаковой длины стробцов.

aij- элемент матрицы, который находится в i-ой строке и j-м столбце.

Вид матрицы: квадратная

Квадратная матрица - это матрица с равным числом столбцов и строк.

Сложение матриц

Сложение матриц А+В есть операция нахождения матрицы С, все элементы которой равны попарной сумме всех соответствующих элементов матриц А и В, то есть каждый элемент матрицы равен Сij=Aij + Bij

Свойства сложения матриц:

1.коммутативность: A+B = B+A;

2.ассоциативность: (A+B)+C =A+(B+C);

3.сложение с нулевой матрицей: A + Θ = A;

4.существование противоположной матрицы: A + (-A) = Θ;

Все свойства линейных операций повторяют аксиомы линейного пространства и поэтому справедлива теорема:

Множество всех матриц одинаковых размеров mxn с элементами из поля P (поля всех действительных или комплексных чисел) образует линейное пространство над полем P (каждая такая матрица является вектором этого пространства).

 

Умножение матрицы на число

Умножение матрицы А на число ¥ (обозначение: ¥A) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен: Bij=¥Aij

 

Свойства умножения матриц на число:

1. 1A = A;

2. (λβ)A = λ(βA)

3. (λ+β)A = λA + βA

4. λ(A+B) = λA + λB

 

Вектор-строка и вектор-столбец

Матрицы размера m x 1 и 1 x n являются элементами пространств K^n и K^m соответственно:

матрица размера m x1 называется вектор-столбцом и имеет специальное обозначение:

 

матрица размера 1 x n называется вектор-строкой и имеет специальное обозначение:

58. Матрицы. Сложение умножение матриц. Матрицы как кольцо, свойства кольца матриц.

Матрицей называется прямоугольная таблица чисел, состоящая из m одинаковой длины строк или n одинаковой длины стробцов.

aij- элемент матрицы, который находится в i-ой строке и j-м столбце.

Вид матрицы: квадратная

Квадратная матрица - это матрица с равным числом столбцов и строк.

Сложение матриц

Сложение матриц А+В есть операция нахождения матрицы С, все элементы которой равны попарной сумме всех соответствующих элементов матриц А и В, то есть каждый элемент матрицы равен Сij=Aij + Bij

Свойства сложения матриц:

1.коммутативность: A+B = B+A;

2.ассоциативность: (A+B)+C =A+(B+C);

3.сложение с нулевой матрицей: A + Θ = A;

4.существование противоположной матрицы: A + (-A) = Θ;

Все свойства линейных операций повторяют аксиомы линейного пространства и поэтому справедлива теорема:

Множество всех матриц одинаковых размеров mxn с элементами из поля P (поля всех действительных или комплексных чисел) образует линейное пространство над полем P (каждая такая матрица является вектором этого пространства).

Умножение матриц

Умножение матриц (обозначение: АВ, реже со знаком умножения А х В) — есть операция вычисления матрицы С, каждый элемент которой равен сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

 

Количество столбцов в матрице А должно совпадать с количеством строк в матрице В, иными словами, матрица А обязана быть согласованной с матрицей В. Если матрица А имеет размерность m x n, B — n x k, то размерность их произведения AB=C есть m x k.

Свойства умножения матриц:

1.ассоциативность (AB)C = A(BC);

2.некоммутативность (в общем случае): AB BA;

3.произведение коммутативно в случае умножения с единичной матрицей: AI = IA;

4.дистрибутивность: (A+B)C = AC + BC, A(B+C) = AB + AC;

5.ассоциативность и коммутативность относительно умножения на число: (λA)B = λ(AB) = A(λB);

59.*Обратимые матрицы. Особенные и неособенные элементарные преобразования строк матрицы. Элементарные матрицы. Умножение на элементарные матрицы.

Обратная матрица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Элементарными преобразованиями строк называют:

• перестановка местами любых двух строк матрицы;
• умножение любой строки матрицы на константу , ;
• прибавление к любой строке матрицы другой строки.

Аналогично определяются элементарные преобразования столбцов.

Элементарные преобразования обратимы.

Обозначение указывает на то, что матрица 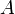может быть получена из 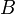путём элементарных преобразований (или наоборот).

Определение. ^ Элементарной матрицей I-го типа называется (п,п)-матрица Р_i,j(с) = Е + сE_i,j, i ¹ j.

Элементарной матрицей II-го типа называется (п,п)-матрица Р_i,j= E_1,1+E_2,2+…+ E_i-1,i-1+ E_i,j+ E_i+1,i+1+…+E_j-1,j-1+E_j,i+E_j+1,j+1+

+…+ E_n,n = E - E_i,i - E_j,j + E_i,j + E_j,i, при i ¹ j.

Элементарной матрицей III-го типа называется диагональная (п,п)-матрица Р_i (c) = diag(1,1,…,c,…,1) =

= E_1,1 + E_2,2 + … + cE_i,i + … + E_n,n = Е + (с – 1)E_i,i, где с ¹ 0.

Умножение матриц (обозначение: , реже со знаком умножения ) — есть операция вычисления матрицы , каждый элемент которой равен сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

Количество столбцов в матрице должно совпадать с количеством строк в матрице 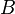, иными словами, матрица обязана быть согласованной с матрицей 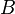. Если матрица имеет размерность , 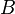— , то размерность их произведения есть .

Свойства умножения матриц:

• 1.ассоциативность (AB)C = A(BC);

• 2.некоммутативность (в общем случае): AB 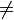BA;

• 3.произведение коммутативно в случае умножения с единичной матрицей: AI = IA;

• 4.дистрибутивность: (A+B)C = AC + BC, A(B+C) = AB + AC;

• 5.ассоциативность и коммутативность относительно умножения на число: (λA)B = λ(AB) = A(λB);

 

 

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: