Четкие отображения и функции

Если некоторым элементам множества А соответствуют некоторые элементы множества В, то множество упорядоченных пар формирует подмножество прямого произведения множеств А и В,

т. е. {(x, y)| xÎA и yÎB}Í(АÄВ). Множество A называют областью отправления, а множество B - областью прибытия.

На рис. 1.1 показаны области отправления A={a, b, c, d, e, f} и прибытия – B={1, 2, 3, 4, 5, 6}.

Проекция на первую компоненту пары {p₁(x, y)} формирует область определения A⁰={a, b, c, d, f}Í A, а на вторую {p₂(x, y)} - область значений B⁰={1, 2, 4, 5, 6}Í B. Элемент y_jÎB⁰ есть образ элемента х_iÎA⁰, а элемент х_iÎA⁰ - прообраз элемента y_jÎB⁰.

Если хотя бы для одного элемента х_iÎA⁰ существует несколько образов, то {(x, y)|xÎA,yÎB}Í (AÄB) называют соответствием.

Например, на рис. 1.1. представлено соответствие, т. к. есть

(c, 1), (c, 6), (d, 4), (d, 5).

Соответствие - это, как правило, двуязычные словари, когда словам одного языка (множество А), как правило, соответствуют несколько слов другого языка (множество В). Например, capacity – способность, мощность, емкость, array – массив, таблица, расположение, scanner - лексический анализатор, устройство для ввода изображений и т. д.

Если для каждого элемента х_iÎA⁰ существует единственный образ, то такое множество упорядоченных пар называют отображением.

Например, в компьютере каждая буква, цифра или символ отображаются в уникальную 8-битовую кодовую комбинацию: “F”:=01000110,.. “s”:=01110011,.. ”Ф”:=11000100,.. “я”:=11001111,.. “5”:=00110101,.. “+”:=00101011,.. “&”:=00100110,.. “{“:=01111011 и т.д.

Единственное отображение принято обозначать t=(x, y), а их множество h={(x, y)|xÎA, yÎB}Í(AÄB).

Если область определения задана на нескольких множествах Хi, то каждое отображение есть кортеж t=(x1, x2,..,xn, y), а их множество

h={(x₁, x₂,..,x_n, y)| x_iÎX_i, yÎY}Í((X₁ÄX₂Ä..ÄX_n)ÄY).

В этом случае y_jÎY⁰ является образом для (x_1i, x_2i,..,x_ni)Î(X₁ÄX₂Ä..ÄX_n), а (x_1i, x_2i,..,x_ni)Î(X₁ÄX₂Ä..ÄX_n) - прообразом для y_jÎY⁰.

Если X₁=X₂=..=X_n=X, то h={(x₁, x₂,..,x_n, y)| x_iÎX, yÎY}Í(XⁿÄY).

Отображение удобно представлять в операторной форме:

h: Xⁿ®Y,

где h -оператор отображения.

Отображение логически совпадает с понятием функция

f=(x, y) или f=(x₁, x₂,..,x_n, y). В этом случае элементы х и (x₁, x₂,..,x_n) называют аргументами, а y – значением функции y=f(x) или y=f(x₁, x₂,..,x_n).

Например, f₊=(x₁, x₂, y) есть y=x₁+x₂ или f_sg=(x, y) есть y=sg(x).

Множество, связывающее значения аргументов и значения функции, называют графиком функции.

Мощность отображения не больше мощности прямого произведения, т.е.

|h|£|X₁|_*|X₂|_*.._*|X_n|_*|Y|.

Каждому отображению h может быть найдено обратное отображение: h^-1: YXⁿ или h^-1={(y, x₁, x₂,..x_n)| x_iÎX, yÎY}Í(YÄXⁿ).

Обратное отображение удобно применять при формировании таблиц реляционных баз данных (см. табл.1.3), когда в “шапке” указывают для каждого столбца имя соответствующей атрибута - I_y, I_x1, I_x2,..I_xn, а в “теле” записывают их значения.

 

В таблице 1.4 дан фрагмент “Журнала заказов..”. В первом столбце приведен уникальный код заказа (Iy), а в остальных указаны атрибуты клиента.

таблица 1.4.

Код	Клиент	Дата	Город	Индекс
	Bolido Comidas preparadas	10-ноя	Мадрид
	Berglunds snabbkop	16-фев	Лулео	S-958 22
	Blauer Delikatessen	27-фев	Мангейм
	Antonio Moreno Taqueria	28-фев	Мехико
	Alfreds Futterkiste	09-май	Берлин
...	...	...	...	...

 

Функция, принимающая значение на двухэлементном множестве {“истина”, “ложь”} или {1, 0}, называется предикатом. В тексте ее обозначают Р(х) или Р(x₁, x₂,..,x_n).

Например, если на множестве целых чисел задать предикаты: Р₁(х):-”x - простое число”, Р₂(x_i, x_j):- ”x_i и x_j имеют общий делитель”, Р₃(f₊(x_i, x_j), x_k):- ”x_k,больше суммы x_i и х_j”, то для x₁=3, х₂=4 и х₃=8 имеем Р₁(3)=“истина”, Р₁(4)=“ложь”, Р₁(8)=“ложь”, Р₂(3, 4)=“ложь”, Р₂(3, 8)=“ложь”, Р₂(4, 8)=“истина”, Р₃(f₊(3, 4), 8)=“истина”;

Значения предикатов удобно описывать двухмерными таблицами, каждая клетка которых содержит “1”, если выполняется логическое условие, и “0” в противном случае. Например, для Р₂(x_i, x_j) см. таблицу 1.5.

 

таблица 1.5.
Р2(xi, xj)

Если даны два отображения h₁ и h₂, то в результате присоединения справа к каждому кортежу первого отображения каждого кортежа второго отображения формируются кортежи нового отображения h, как результат прямого произведения h₁ и h₂, т. е.

 

h=(h¹Äh²)={(y¹;x₁¹;x₂¹;...x_n¹;y²;x₁²;x₂²;...x_n²)|yÎ(Y¹ÈY²), x_i¹ÎX¹; x_i²ÎX²}.

Операторная запись прямого произведения имеет вид:

h:=product(h¹, h²)

Число строк формируемого отображения равно произведению числа кортежей первого и второго отображений, а его ранг равен сумме рангов первого и второго отображений.

Нечеткие отображения

Наряду с нечеткими множествами существуют нечеткие отображения h: X Y, когда четко заданы носители отображения (X и Y) и нечетко – принадлежность каждой пары (x, y) нечеткому отображению h’.

Значение функции принадлежности (x_i, y_j)Î(XÄY) есть степень принадлежности нечеткому отображению h’, т. е.

h’={m_h’(x_i, y_j)/ (x_i, y_j)| x_i ÎX, y_jÎY}.

Нечеткие отображения удобно описывать матрицами, строки которой есть xÎX – прообразы нечеткого отображения, а столбцы - yÎY – образы нечеткого отображения. Тогда в клетках (x_i, y_j) будут указаны значения их степени принадлежности m_h’(x_i, y_j).

 

Пример. Пусть в пределах региона необходимо разместить двенадцать магазинов розничной торговли Х = {x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀, x₁₁, x₁₂}, представляющих четыре фирмы оптовой торговли Z = { z₁, z₂, z₃, z₄ }. Руководители фирм обратились в консалтинговую фирму для построения рациональной структуры использования и размещения магазинов в регионе.

Пусть эксперты установили, что на структуру использования и размещения магазинов наибольшее влияние оказывают “доступность мага­зина" (y₁), “высокое качество товара” (y₂), “высокий уровень обслуживания” (y₃) и “низкие цены” (y₄), т.е. Y={y₁, y₂, y₃, y₄}.

Эксперты, обсуждая с руководителями магазинов и фирм организацию торговли, установили их нечеткое понимание значимости пожеланий покупателя.

Пусть учет принятых показателей руководителями магазинов представлен, как нечеткое отображение X Y таблицей 1.6, где каждый x_i дал нечеткую оценку значимости каждого показателя.

График нечеткого отображения мнения руководителя магазина о каждом пожелании покупателя есть:

h_i’₁={m_h’(x_i, y₁)/ (x_i, y₁), m_h’(x_i, y₂)/ (x_i, y₂), m_h’(x_i, y₃)/ (x_i, y₃), m_q’(x_i, y₄)/ (x_i, y₄)}.

Прообразом, например, для y₁ является нечеткое множество

X'_y1={1,0/ x₁, 0,8/x₆, 0,7/ x₇, 0,5/ x₈, 0,5/ x₉, 0,6/ x₁₀, 0,1/ x₁₁}, а образом, например, для x₆ является нечеткое множество Y_x6’={0,8/ y₁, 0,4/ y₂, 0,5/ y₃, 0,9/ y₄}.

таблица 1.6.
h’1	y1	y2	y3	y4
x1
x2
x3
x4
x5
x6	0,8	0,4	0,5	0,9
x7	0,7	0,3	0,4	0,8
x8	0,5	0,8	0,8	0,2
x9	0,5	0,5	0,5	0,5
x10	0,6	0,7	0,8	0,5
x11	0,1	0,1	0,1	0,1
x12

Для x₁ значимым является только “доступность магазина” (y₁), для x₂ – “высокое качество товара” (y₂), для x₃ –“высокий уровень обслуживания” (y₃), для x₄ –“низкие цены” (y₄). Для x₅ - важны все признаки. Для x₈ - наибольшее значение имеют “высокое качество товара” (y₂) и “высокий уровень обслуживания (y₃), степень принадлежности которых равна 0,8. Для x₉ – все признаки имеют не очень большое значение, так как степень принадлежности равна 0,5, а для x₁₁ - все они совершенно незначимы, так как степень принадлежности равна 0,1.

Пусть таблицей 1.7 представлены мнения руководителей фирм о значимости каждого показателя.

График нечеткого отображения мнения руководителя фирмы о каждом показателе есть

h_j’₂={m_h’(y₁, z_j)/ (y₁, z_j), m_h’(y₂, z_j)/ (y₂, z_j), m_h’(y₃, z_j)/ (y₃, z_j), m_h’(y₄, z_j)/ (y₄, z_j)}.

Прообразом, например, для y₁ будет нечеткое множество

Z’_y1={0,9/ z₁, 0,1/ z₂, 0,5/z₄, 0,7/ z₄}, а образом, например, для z₄ будет нечеткое множество Y’_z4={0, 7/ y₁, 0,6/ y₂, 0,4/ y₃, 0,6/ y₄}.

таблица 1.7.
h’2	z1	z2	z3	z4
y1	0,9	0,1	0,5	0,7
y2	0,5	0,9	0,6	0,6
y3	0,4	0,9	0,5	0,4
y4	0,8	0,1	0,5	0,6

Например, для z₁ наиболее значимы “доступность магазина” (y₁) и “низкие цены” (y₄), для z₂ –“высокие качество товара” (y₂) и “высокий уровень обслуживания” (y₃), для z₃ – все они не имеют большого значения, для z₄ –незначим “высокий уровень обслуживания” (y₃).

Отношение

Упорядоченные кортежи, компоненты которых принадлежат одному множеству, называют отношением. Например, (x_i, x_j, x_k,..).

Отношениями между математическими объектами могут быть элементы Q₁ = {=, ¹, ³, >, <, £}. Например, “2=2”, “3>2”.

Отношениями между “нематематическими” объектами могут быть элементы Q₂ = {”..принадлежит..”, “..часть..”, “..смежный..”, “.. родственник..”, “..родитель..”, “..находится рядом с..”, и т. д.}.

Например, “двигатель <тип> часть автомашины <тип>”, “судно <имя> находится рядом с причалом <номер>”, ”игорь родитель святослава” и т.п.

Отношения, как и отображения, могут быть четким (relation) и и нечеткими (fuzzi relation).

Четкие отношения

Упорядоченные кортежи, сформированные из элементов одного множеств, формируют отношение:

r={(x₁, x₂,..,x_n)| x_iÎX}ÍXⁿ.

Если n=1, то отношение называют унарным или одноместным. Такое отношение r(x) равносильно заданию предиката Р(х) на области определения для формирования подмножества, удовлетворяющего заданному условию.

Например, r={x| P(x):=”x-простое число”, для xÎ{1,2, 3,..20}}=

{2, 3, 5, 7, 11, 13, 17, 19}

Если n=2, то отношение называют бинарным или двухместным. Такое отношение позволяет сравнивать по предикату P(x_i, x_j) элементы множества X.

Например, r={(x_i, x_j)| P₂(x_i, x_j):=”(x_i, x_j ) имеют общий делитель” для xÎ{2, 3, 4, 5, 6, 7, 8}}={(2, 4), (2, 6), (2, 8), (3,6)}.

Если n=3, то отношение называют терарным или трехместным.

Такое отношение позволяет сравнивать по заданному предикату P(x_i, x_j, x_k) элементы множества X.

Например, r={(x_i, x_j, x_k)| P(x_i, x_j, x_k):=”(x_k:=<число>, x_j:=<месяц>, x_k:=<год>)”.

Или r={(x_i, x_j, x_k)| P(x_i, x_j, x_k):=”x_k:= (x_i×x_j)” для xÎ{2, 3, 4, 5, 6, 7, 8}} = {(2, 3, 6), (2, 4, 8)}.

Если n=n, то отношение называют n-арным или n-местным.

Отношения удобно представлять в операторной форме:

r: X®X или r: X^n-1®X.

Бинарные отношения между элементами множества X удобно описывать матрицами (ХÄХ), строки и столбцы которых есть элементы множества X, а на пересечении i-ой строки и j-го столбца ставят знак “1”, если дано отношение r(x_i, x_j) и “0” в противном случае, т.е.

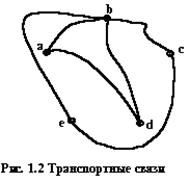
Пример. между пунктами a, b, c, d, e есть транспортные связи, как показано на рис. 1.2. Эти связи отображены в таблице 1.8.

 

 

Если даны два отношения r₁ и r₂, то может быть сформировано их прямое произведение, как новое отношение r=(r₁Är₂), носителем которого являются (x_i¹, x_j²)Î(X₁ÄX₂), a r((x_i¹, x_m²), (x_k¹, x_j²))=1 тогда и только тогда, когда r₁(x_i¹, x_k¹)=1 и r₂(x_m², x_j²)=1.

r=(r₁Är₂)={((x_i¹, x_m²⁾, (x_k¹, x_j²))| x_i¹, x_k¹ÎX₁ и x_m², x_j²ÎX₂}.

Операторная запись прямого произведения имеет вид:

r=product(r₁, r₂).

Анализ множества отношений позволяет выделить свойства, наличие которых характеризует определенный класс отношений.

Бинарное отношение рефликсивно, если для каждого х_iÎХ имеем r(x_i; x_i)=1. Такими отношениями являются “..=..”, “..быть похожим..”, “..быть изоморфным..”, “..быть эквивалентным..” и т.п. При матричном описании такого отношения на главной диагонали матрицы будут только “1”, т.е. r(x_i, x_i)=1.

Бинарное отношение антирефлексивно, если для каждого х_iÎХ имеем r(x_i, x_i)=0.

Такими отношениями являются “..>.. ”, “..<..”, “..быть родителем..”, “..быть частью..” и т.п..

При матричном описании такого отношения на главной диагонали матрицы будут только “0”, т.е. r(x_i, x_i)=0.

Бинарное отношение симметрично, если для любой пары (x_i, x_j)ÎR при i¹j имеем r(x_i, x_i)=r(x_j, x_i)=1. Такими отношениями являются “..¹..”, “..быть похожим..”, “..быть эквивалентным..”, “..быть родственником..” и т.п.. При матричном задании такого отношения будет симметричное расположение “1” относительно главной диагонали, т.е. r(x_i, x_i)=r(x_j, x_i).

Бинарное отношение антисимметрично, если для любой пары (x_i, x_j) при i¹j имеем r(x_i, x_i)¹r(x_j, x_i), а при i=j имеем r(x_i, x_i)=1. Такими отношениями являются “..³..”, “..£..” и т.п.. При матричном задании такого отношения это означает несимметричное расположение “1” относительно главной диагонали и наличие “1” на главной диагонали.

Бинарное отношение асимметричн о, если для любой пары (x_i, x_j) при i¹j имеем r(x_i, x_i)¹r(x_j, x_i), а при i=j имеем r(x_i, x_i)=0.. Такими отношениями являются “..>..”, “..<..”, “быть родителем” и т.п. При матричном задании такого отношения это означает несимметричное расположение “1” относительно главной диагонали и наличие “0” на главной диагонали.

Бинарное отношение транзитивно, если для любых элементов x_i, x_j, x_kÎХ r(x_i, x_i)=1 тогда и только тогда, когда r(x_i, x_k)=1 и

r(x_k, x_i)=1. Такими отношениями являются “..>..”, “..<..”, “быть родителем”, “быть родственником” и т.п..

Наиболее изученными классами отношений являются отношения эквиваленции, частичного и строгого порядка.

Бинарное отношение, удовлетворяющее условиям рефлексивности, симметричности и транзитивности формируют класс отношений эквиваленции.

Такими отношениями являются “..=..”, “..быть похожим..”, “..быть родственником..”.

Отношение эквиваленции обозначают r_~(x_i, x_i) или ~(x_i, x_i). Это отношение позволяет выделять из множества Х классы элементов по образцу х_a, т.е.

K_a ={x| r_~(x, x_a)=1, x, x_aÎX}ÍX.

Формирование классов эквиваленции K_a1, K_a2,...K_an разбивает все множество Х на подмножества, т.е.

Х={Х_a1, Х_a2,..,Х_an}.

Бинарные отношения, удовлетворяющие условиям рефлексивности, антисимметричности и транзитивности формируют класс отношений частичного порядка.

Такими отношениями являются “..³..”, “..£..”, “..быть не старше..” и т.п.

Отношение частичного порядка обозначают для элементов r_£(x_i, x_i) или £(x_i, x_i), а для подмножеств r_Í(X_i, X_j) или Í(X_i, X_j). Отношение £(x_i, xj) позволяет установить частичный порядок элементов множества X, а отношение Í(X_i, X_j) – частичный порядок подмножеств множества X.

Пример: даны множества U={1, 2, 3, 4, 5, 6}, X₁={1, 2, 3, 4}, X₂={2, 3, 4, 5}, X₃={2, 3, 4}, X₄={3, 4, 5}, X₅={2, 3}, X₆={3, 4}, X₇={4, 5},

X₈={2, 4}. Какой между ними может быть установлен порядок?

Анализ следует начинать с множеств, имеющих наименьшее число элементов. Тогда X₈ÍX₃ÍX₂ÍU или X₈ÍX₃ÍX₁ÍU, X₇ÍX₄ÍX₂ÍU, X₆ÍX₄ÍX₂ÍU или X₆ÍX₃ÍX₂ÍU или X₆ÍX₃ÍX₁ÍU, X₅ÍX₃ÍX₂ÍU, X₅ÍX₃ÍX₁ÍU.

Бинарное отношение, удовлетворяющее условиям антирефлексивности, асимметричности и транзитивности, формирует класс отношений строго порядка.

Такими отношениями являются “..>..”, “..<..”, “..быть родителем..”, “быть частью”, “быть подчиненным” и т.п. Отношение строгого порядка для элементов множества r_<(x_i; x_i) или <(x_i; x_i), а для подмножеств множества: r_Ì(X_i; X_j) или Ì(X_i; X_j).

Примерами строгого порядка являются целые числа, упорядоченные правилом n=(n+1), или буквы, упорядоченные алфавитом, и т.п.

Нечеткое отношение

Наряду с нечеткими отображениями существуют нечеткие отношения , когда четко заданы элементы множества X, а значение функции принадлежности m_r’(x_i, x_j)/(x_i, x_j) каждой пары элементов (x_i, x_j)ÎXÄX или степень принадлежности формирует нечеткое отношение: r’={m_r’1(x_i, x_j)/(x_i, x_j)| x_i,x_jÎX}.

Нечеткие отношения удобно описывать с помощью матриц, строки которых есть прообразы нечеткого отношения, а столбцы – образы. Тогда в клетках таблицы (x_i, x_j) будут указаны m_h’(x_i, x_j).

Если дано n-арное отношение r’(x₁, x₂, ¼,x_n): X^n-1®X, то значение функции принадлежности должно быть найдено для каждого набора (x_1i, x_2i, ¼,x_ni), т.е.

r’={m_r’ (x₁, x₂, ¼,x_n)/(x₁, x₂, ¼,x_n)| x₁, x₂,..x_nÎX}.

Пример: пусть в результате стихийного бедствия нарушились транспортные связи между населенными пунктами a, b, c, d, e. Эксперты установили степень принадлежности нечеткому отношению смежности между населенными пунктами, как показано на рис.1.3 и в таблице 1.9.

 

Для нечетких отношений также могут быть определены свойства нечетких рефлексивности, симметричности и транзитивности, которые позволят формировать классы нечетких отношений. Подробнее о вычислении нечетких классов см. 1.7.

 

1.4. Элементы общей алгебры

Одной из важных характеристик упорядоченного множества является наличие граней. Если среди элементов множества X задан частичный порядок £(x_i, x_j), то найдется такой элемент x_a, для которого выполняется условие £(x_i, x_a) для любого x_iÎX и найдется такой элемент x_b, для которого выполняется условие £(x_b, x_i) для любого x_iÎX.

Наименьший элемент из нескольких x_a формирует верхнюю грань упорядоченного множества:

min{x_a}=SupX_i, где X_i={x_i, x_j}.

Наибольший элемент из нескольких x_b формирует нижнюю грань упорядоченного множества:

max{x_b}=Inf X_i, где X_i={x_i, x_j}.

Для строго упорядоченных множеств x_aÏX_i и x_bÏX_i, а для частично упорядоченных x_a=max{x_iÎX_i} и x_b=minx_iÎX_i}.

Поиск граней есть операции над множествами.

Поэтому множество и операций над его элементами формируют общую алгебру, т.е.

A=<X; F>,

где X={x₁, x₂,..x_m} - носитель алгебры,

F={f₁, f₂,..f_k} - cигнатура алгебры, содержащая унарные и бинарные операции.

Унарные операции имеют один операнд x_iÎX, а бинарные операции - два x_i, x_jÎX.

Результаты исполнения операций принадлежат тому же множеству X.

Для общей алгебры справедливы аксиомы:

· коммутативности: x_if_kx_j = x_jf_kx_i; операнды одной операции f_k можно менять местами,

· ассоциативности: x_if_k(x_jf_kx_k) = (x_jf_kx_j)f_kx_k; при исполнении одной бинарной операции f_k над несколькими операндами скобки можно не расставлять, а операции исполнять в любом порядке,

· дистрибутивности: x_if_k(x_jf_mx_k) = (x_if_kx_j)f_m(x_if_kx_k); при исполнении двух бинарных операций f_k и f_m над различными операндами первая операция f_k исполняется с каждым операндом второй операции f_m, а вторая операция f_m с результатами исполнения первой операции f_k,

· идемпотентности: x_if_kx_i = x_i; результатом исполнения бинарной операции f_k над одним и тем же операндом x_i будет значение операнда,

· поглощения: x_if_k(x_if_mx_j)=x_i; результатом исполнения двух различных бинарных операций f_k и f_m, но содержащих общий операнд x_i, будет значение операнда x_i.

Булева алгебра

Если элементы множества X принимают значения из множества {0, 1} и упорядочены отношением £(x_i, x_i), то

а)операцию поиска верхней грани называют дизъ юнкцией, оператор которой обозначают так: “Ú”, т.е. SupX=(x_iÚx_j),

b) операцию поиска нижней грани называют конъюнкцией, оператор которой обозначают “×” или “&”, т. е. Inf X=(x_i×x_j) или

Inf X=(x_i&x_j).

с) операцию поиска дополнения элемента x на множестве

{0, 1} называют отрицанием, оператор которой обозначают “` “ или “ù “, т. е. not(x)=`x или not(x)=ùx.

Алгебра, использующая операции дизъюнкции, конъюнкции и отрицания над множеством, элементы которого принимают значения из множества {0, 1}, называется булевой алгеброй в часть английского математика Дж. Буля:

A_.=<X, Ú, ×, `, 0, 1>,

где X – носитель алгебры, а {Ú, ×,` } - сигнатура алгебры.

Операторы конъюнкции, дизъюнкции и отрицания называют также логическими связками.

Булевы операции

Дизъюнкция (x₁Úx₂) есть бинарная операция, значение которой равно 0 в том и только в том случае, когда оба операнда равны 0.

Схема операции имеет вид: f(x_i, x_j)=disjunction(х_i, х_j).

Операцию дизъюнкции можно выполнять на произвольном числе элементов множества X.

Например,

f(х₁, х₂,..х_n)= (х₁Úх₂Ú...Úх_n)= _i=1 Ú ⁿх_i.

 

Конъюнкция (x₁×x₂) есть бинарная операция, значение которой равно 1 в том и только в том случае, когда оба операнда равны 1.

Схема операции имеет вид: f(x_i, x_j)=conjunct(х₁, х₂).

Операцию конъюнкции можно выполнять на произвольном числе элементов множества X.

Например,

f (х₁, х₂,..х_n)= (х₁×х₂×..×х_n)=_i=1&ⁿх_i,

 

Отрицание `x есть унарная операция, значение которой

противоположно значению операнда. Схема операции имеет вид: f(x)=not(x).

Операцию отрицания можно распространить на произвольные формулы булевой алгебры. Например,

f(x₁,x₂,..x_n)=ù(x₁Úх₂Ú...Úх_n)=(x₁Úх₂Ú...Úх_n), f(x₁, x₂,..x_n)=ù(х₁×х₂×...×x_n)=(х₁×х₂×...×x_n).

Законы булевой алгебры

Аксиомы общей алгебры формируют законы булевой алгебры:

· коммутативности: x_iÚx_j=x_jÚx_i и x_i×x_j=x_j×x_i,

· ассоциативности: x_iÚ(x_jÚx_k)=(x_jÚx_j)Úx_k и x_i×(x_j×x_k)=(x_j×x_j)×x_k,

· дистрибутивности: x_iÚ(x_j×x_k)=(x_iÚx_j)×(x_iÚx_k) и x_i×(x_jÚx_k)=(x_i×x_j)Ú(x_i×x_k),

· идемпотентности: (x_iÚx_i)=x_i и (x_i×x_i)=x_i,

· поглощения: x_iÚ(x_i×x_j)=x_i и x_i×(x_iÚx_j)=x_i,

· противоречия: (xÚ`x)=1 и (x×`x)=0,

· двойного отрицания: ù(`x)=x,

· склеивания: x×FÚ`x×F=F, (xÚF)×(`xÚF)=F,

· де Моргана: ù(x_iÚx_j)=`x<sub>i</sub>×`x_j и ù(x_i×x_j)=`x<sub>i</sub>Ú`x_j,

· Порецкого xÚ`x×y=xÚy, x×(`xÚy)=x×y,

· константы: (xÚ0)=x, (x×0)=0,

(xÚ1)=1, (x×1)=x.

Формула булевой функции

Функцию y=f(x₁, x₂,..x_n), значение которой и значения компонент аргумента принадлежат множеству {0, 1}, называют булевой, а аргумент – булевым вектором. Компоненты булевого вектора называют булевыми (или двоичными) переменными.

Алгебраическое выражение булевой функции, использующее только булевы переменные булевого вектора и только логические связки конъюнкции, дизъюнкции и отрицания, называют формулой.

Если даны булевы переменные x_i, x_j, то элементарными формулами являются F=`x_i, F=ùx_j, F=(x_iÚx_j), F=(x_i×x_j), а производными формулами F=ùF, F=(F_iÚF_j), F=(F_i×F_j).

Для описания функции формулами используют два правила: подстановки и замещения.

Пусть даны равносильные формулы F_i и F_j, т. е. (F_i=F_j), которые содержат переменную x. Если всюду в формулы F_i и F_j вместо x подставить произвольную формулу F, то будут получены также равносильные между собой формулы F’_i и F’_j, т. е. F’_i=F’_j.

Пусть дана формула (F_i=F_j) и существует формула F_k, равносильная только одной подформуле F_i, т. е. (F_i=F_k). Тогда F_i может быть замещена формулой F_k и получена новая формула (F_k=F_j). При этом не обязательно ее замещение всюду в алгебраическом выражении булевой функции.

Описание булевой функции

При табличном описании булевой функции необходимо для каждого набора двоичного переменных булевого вектора указывать её значение. Если значение функции определено не для всех наборов булевого вектора, то функцию называют частично определённой.

Число строк таблицы детерминированной функции от n компонентов аргумента равно 2ⁿ.

таблица 1.13. x1 x2 ¼ xn f(x1;x2;¼…xn) … … …¼ …¼ ¼   … …¼

При аналитическом описании булевой функции используют элементарные унарные и бинарные операторы булевой алгебры, а также правила подстановки и замещения при формировании формул булевой функции.

Число логических функций для n компонентов аргумента определяется выражением: 2^p, где p=2ⁿ.

таблица 1.14. X y=f(x)   f0(x) f1(x) f2(x) f3(x)

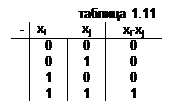
Для n=1 число возможных значений логической функции равно 4 (см. табл. 1.14).

Анализ таблицы позволяет дать определение каждой из четырёх логических функций:

 

· f₀(x) – функция-константа “0”, т.к. она не изменяет своего значе- ния при изменении аргумента, т.е. (y=0);

· f₁(x) – функция-повторитель, т.к. она принимает значения, равные значению аргумента, т.е. (y=x);

· f₂(x) - функция-инверсия (или отрицания), т.к. она принимает значения противоположные значению аргумента, т.е. (y=`x);

· f₃(x) - функция-константа “1”, т.к. она не изменяет своего значения при изменении аргумента, т.е. (y=1).

таблица 1.15 Аргумент Функция y=fi(x1, x2) x1 x2 f0 f1 f2 f3 f4 f5 f6 f7 f8 f9 f10 f11 f12 f13 f14 f15

Для n=2 число возможных значений логической функции равно 16 (см. табл. 1.15).

В таблице 1.16 приведены алгебраические выражения функции по законам булевой алгебры. Некоторые функций имеют достаточно сложное алгебраическое описание.

Например для f₆(x₁;x₂) и f₉(x₁;x₂).

таблица 1.16.   y=f(x1; x2) Формула логической функции в базисе булевой алгебры. y=fi(x1; x2) f(0;0) f(0;1) f(1;0) f(1;1)           y=f0(x1; x2)=0 – константа “0”         y=f1(x1; x2)=(x1×x2) – конъюнкция         y=f2(x1; x2)=(x1×`x2) - конъюнкция         y=f3(x1; x2)=x1 =повторитель         y=f4(x1; x2)=(`x1×x2) - конъюнкция         y=f5(x1; x2)=x2 - повторитель         y=f6(x1; x2)=(x1×`x2)Ú(`x1×x2) –дизъюнкция конъюнкций         y=f7(x1; x2)=x1Úx2 - дизъюнкция         y=f8(x1; x2)=ù(x1Úx2)) – отрицание дизъюнкции         y=f9(x1; x2)=(x1×x2)Ú(`x1×`x2) - дизъюнкция конъюнкций         y=f10(x1; x2)=`x2 - инверсия         y=f11(x1; x2)=x1Ú`x2 дизъюнкция         y=f12(x1; x2)=`x1 -инверсия         y=f13(x1; x2)=`x1Úx2 -дизъюнкция         y=f14(x1; x2)=ù(x1×x2) –отрицание конъюнкции         y=f15(x1; x2)=1 – константа “1”

Поэтому в развитие булевой алгебры в алгебре логики введены дополнительные логические связки:

· «- экви

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: