 |
Сформулируйте и докажите теорему сложения вер-тей для любых событий A и B. Что такое правило сложения вер-тей для несовместных соб. A и B?
|
|
|
|
Пространство элемент. событий? случ соб? исходы благоприятные для А? вероятность А? примеры. Можно ли в опыте с бросанием игральной кости считать элемент. события: А – выпадение числа очков, меньших 2; В – выпадение более 2 очков?
Пространством элемент событий называется мн-во  (омега), состоящее из исходов или элемент событий
(омега), состоящее из исходов или элемент событий  , из кот происходит одно. Случ событие - любое подмн-во пространства элемент. событий А
, из кот происходит одно. Случ событие - любое подмн-во пространства элемент. событий А  . Исходы
. Исходы 
 А – благоприятны для события А. Событие А наступило, если в опыте наблюдался один из благоприятных исходов. Р случ события А - отношение числа благоприятных исходов k к общему числу исходов n: P(A) =
А – благоприятны для события А. Событие А наступило, если в опыте наблюдался один из благоприятных исходов. Р случ события А - отношение числа благоприятных исходов k к общему числу исходов n: P(A) =  (классич определении Р). Пример. В опыте с подбрасыванием монеты пространство элементарных событий состоит из двух исходов
(классич определении Р). Пример. В опыте с подбрасыванием монеты пространство элементарных событий состоит из двух исходов  =
=  , вероятность выпадания герба А=
, вероятность выпадания герба А=  равна P(A)=0.5. Пространство элемент. событий состоит из 6 исходов
равна P(A)=0.5. Пространство элемент. событий состоит из 6 исходов  =
=  . Т.е. А =
. Т.е. А =  , В=
, В=  . А- это элементарное событие, тк состоит из 1 элементарного события; В – не будет элементарным событием, тк состоит из др. элементарных событий.
. А- это элементарное событие, тк состоит из 1 элементарного события; В – не будет элементарным событием, тк состоит из др. элементарных событий.
4. достоверные и невозможные соб., их вероятности? Пусть A, B и C – случ соб. Перечислите все случаи наступления события  .
.
Достоверное - кот произойдет при любом испытании А =  . Например, в опыте с подбрасыванием кости А, задаваемое условием “число выпавших очков положительное”, будет достоверным. Р = 1. Невозможное - кот не может произойти при испытании А= V или ø. Например, событие А, задаваемое условием “при подбрасывании кости выпало 7 очков”, является невозможным. Р =0.
. Например, в опыте с подбрасыванием кости А, задаваемое условием “число выпавших очков положительное”, будет достоверным. Р = 1. Невозможное - кот не может произойти при испытании А= V или ø. Например, событие А, задаваемое условием “при подбрасывании кости выпало 7 очков”, является невозможным. Р =0.
Таблица, характеризующая событие А  +С
+С
| А | В | С | А  +С +С
|
|
|
|
5.В каком случае событие В называют следствием события А? Какие события называются равными? Объясните, почему  .
.
Соб А влечет за собой соб В или В является следствием соб А (А  В), если каждый исход, благоприят для А, является благоприят и для В. Соб А и В равны (А=В) в случае, когда они являются следствиями друг друга. I)А
В), если каждый исход, благоприят для А, является благоприят и для В. Соб А и В равны (А=В) в случае, когда они являются следствиями друг друга. I)А  АВ+А
АВ+А  .Если А наступило(А=1), то: 1) если В при этом наступило, то наступило АВ
.Если А наступило(А=1), то: 1) если В при этом наступило, то наступило АВ  АВ+А
АВ+А  наступило; 2) если В не наступило, то
наступило; 2) если В не наступило, то  =1
=1 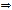 А
А 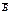 =1
=1  АВ+А
АВ+А  наступило. II) АВ+А
наступило. II) АВ+А 
 А. Если АВ+А
А. Если АВ+А 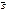 наступило, то либо АВ наступило (т.е А наступило
наступило, то либо АВ наступило (т.е А наступило  АВ+А
АВ+А 
 А) либо наступило А
А) либо наступило А  (А наступило
(А наступило  АВ+А
АВ+А 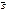
 А). Соб А наступает, т.к. любое соб А попадает в В или
А). Соб А наступает, т.к. любое соб А попадает в В или  . А=А(
. А=А( )=А*
)=А*  =А.
=А.
6. Пусть А и В – случ соб. Упростите  . Найдите соб, противоп ему.
. Найдите соб, противоп ему.
(А+В)(А+  ) = АА+А
) = АА+А  +АВ+В
+АВ+В 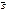 =А+А(В+
=А+А(В+  )
)

7. Докажите, что  . Что обозначает соб
. Что обозначает соб  ?
?
 =
=  *
*  *…..*
*…..*  . Наступление соб А
. Наступление соб А  +….А
+….А  означает, что наступает по меньшей мере одно из соб А
означает, что наступает по меньшей мере одно из соб А  ,….,А
,….,А  . Наступление противоп соб
. Наступление противоп соб  означает, что не наступает ни одно из соб А
означает, что не наступает ни одно из соб А  ,….,А
,….,А  или наступают одновременно все соб
или наступают одновременно все соб  ,….,
,….,  , но это в точности означает наступление соб
, но это в точности означает наступление соб  *
*  *…..*
*…..*  . А
. А  А
А 
 + А
+ А 
 А
А 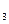 +
+  А
А  А
А 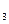 : означает наступление ровно двух соб из трех.
: означает наступление ровно двух соб из трех.
8. Докажите, что  =
=  +
+  +…..+
+…..+  . Что означает соб А
. Что означает соб А  А
А  + А
+ А  А
А 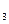 + А
+ А  А
А 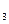 ?
?
 =
=  +
+  +…..+
+…..+  . Наступление соб А
. Наступление соб А  *….*А
*….*А  означает, что наступают каждое из соб А
означает, что наступают каждое из соб А  ,….,А
,….,А  . Наступление противоп соб
. Наступление противоп соб  означает, что не наступает хотя бы одно из собА
означает, что не наступает хотя бы одно из собА  ,….,А
,….,А  или наступают соб
или наступают соб  +
+  +…..+
+…..+  . А
. А  А
А  + А
+ А  А
А 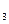 + А
+ А  А
А 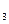 : означает наступление не меньше двух соб или = 2
: означает наступление не меньше двух соб или = 2
9. Сформулируйте статистическое определение Р. Поч Р удовлетворяет условию  ? Возможны случаи Р=0 и Р=1?
? Возможны случаи Р=0 и Р=1?
Р случ соб-положит число, заключенное между 0 и 1. Случ соб благоприятствует лишь часть из общего числа элемент исходов испытания. В этом случае 0<m<n, значит, 0<m/n<1⇒0<P(A)<1. Р любого соб удовлетворяет двойному нер-ву 0≤Р(А)≤1. Статистич Р -относит частота его реализации при большом кол-ве исрытаний m/n. Св-ва Р вытекают из классич определения и сохраняются для статистич. Возможны. А- выпала игральная кость, числа которой > 7, P(A)=0. В- выпала игральная кость, числа которой < 7, P(A)=1
|
|
|
Сформулируйте и докажите теорему сложения вер-тей для любых событий A и B. Что такое правило сложения вер-тей для несовместных соб. A и B?
Теорема слож.Р д ля любых соб. A и B - P(A+B)=P(A)+P(B)-P(AB) сумма Р соб. без Р их совмест наступления. Док-во: Обозначим через n= 

 - общее число исходов, ns- число исходов, благоприятных для соб. S.Тогда формулу
- общее число исходов, ns- число исходов, благоприятных для соб. S.Тогда формулу  =
=  +
+  –
–  можно переписать след. образом nA+B=nA+nB-nAB(*).
можно переписать след. образом nA+B=nA+nB-nAB(*).
Разделив почленно формулу (*) на n, получим формулу P(A+B)=P(A)+P(B)-P(AB)
Правило сложения вер-тей. Если соб. A и B несовместны, то P(A+B)=P(A)+P(B).Док-во:Т.е. соб. A и B несовместны, то P(AB)=0, поэтому из формулы P(A+B)=P(A)+P(B)-P(AB), получим P(A+B)=P(A)+P(B).
11 Какие соб.A1,A2,…An называются попарно несовместными? Сформулируйте правило сложения вер-тей для попарно несовместных соб. A1, A2, …An. Приведите пример попарно несовместных событий A,B, и C, таких что P(A+B+C)<1?
A1,A2,…An – попарно несовместны, если два из них не выполняются одновременно. Исходя из следствия, можно сказать, что вер-ть появления одного из нескольких попарно несовместных соб., безразлично какого, равно сумме вер-тей этих соб. P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An). Док-во: Рассмотрим 3 соб.A,B,C. Т.к. рассматриваемые события попарно несовместны, то появление одного из трех событий, A,B,C, равносильно наступлению одного из двух соб,A+B и C, поэтому в силу указанной теоремы
P(A+B+C)=P  =P(A+B)+P(C) =P(A)+P(B)+P(C). Пример: Существуют 5 карточек с написанными цифрами: 1,2,3,4,5. è
=P(A+B)+P(C) =P(A)+P(B)+P(C). Пример: Существуют 5 карточек с написанными цифрами: 1,2,3,4,5. è 
 . Соб.А – вытащили карточку с числами, делящимися на 2, В – делящ. на 3, С – делящ. на 5. Соб А,В,С попарно независимы. АВ=
. Соб.А – вытащили карточку с числами, делящимися на 2, В – делящ. на 3, С – делящ. на 5. Соб А,В,С попарно независимы. АВ=  , АС=
, АС=  , ВС=
, ВС=  . è P(A+B+C)=P(A)+P(B)+P(C).
. è P(A+B+C)=P(A)+P(B)+P(C).
 ,
,  ,
,  èP(A+B+C)=0,4+0,2+0,2=0,8<1.
èP(A+B+C)=0,4+0,2+0,2=0,8<1.
12 поч Р(А+В)≤Р(А)+Р(В) для соб A и B. Чему = сумма P(A)+P( ) Р противоп соб?
) Р противоп соб?
А и В – как сов., так и несов. события. Р(А+В)=Р(А)+Р(В) - Р(АВ).  Когда мы считаем P(А+В), то при сложении Р(А) и Р(В) мы дважды учитываем пересечение, то есть его надо вычесть: Р(А)+Р(В)=Р(АВ)+Р(А`В)+Р(А+В)- Р(А`В)ÞР(А)+Р(В)=Р(АВ)+Р(А+В); Р(А+В)=Р(А)+Р(В)-Р(АВ); Р(А+В)≤Р(А)+Р(В). Исходя из следствий (теорема сложения Р) можно сказать, что сумма Р противоп соб =1. P(A)+P(
Когда мы считаем P(А+В), то при сложении Р(А) и Р(В) мы дважды учитываем пересечение, то есть его надо вычесть: Р(А)+Р(В)=Р(АВ)+Р(А`В)+Р(А+В)- Р(А`В)ÞР(А)+Р(В)=Р(АВ)+Р(А+В); Р(А+В)=Р(А)+Р(В)-Р(АВ); Р(А+В)≤Р(А)+Р(В). Исходя из следствий (теорема сложения Р) можно сказать, что сумма Р противоп соб =1. P(A)+P( )=1. Т.к. соб A и
)=1. Т.к. соб A и  несовместны, поэтому можно применить формулу P(A+B)=P(A)+P(B). При этом следует использовать то, что соб A+
несовместны, поэтому можно применить формулу P(A+B)=P(A)+P(B). При этом следует использовать то, что соб A+  - достоверное, поэтому его Р =1.Также используют такую формулу, выражающую Р соб A через Р противоп соб
- достоверное, поэтому его Р =1.Также используют такую формулу, выражающую Р соб A через Р противоп соб  . P(A)=1-P(
. P(A)=1-P( )
)
|
|
|
13 Верно ли, что если соб A - следствие события B,то P(A) ≤ P(B)?
Да т.к. согласно следствию: если соб B явл. следствием соб. A, то P(A) ≤ P(B). Т.к. A  B, то B=A+(B/A)- сумма несовместных соб. Применяя правило сложения Р, имеем P(B)=P(A)+P(B/A), откуда следует нер-во P(A) ≤ P(B)
B, то B=A+(B/A)- сумма несовместных соб. Применяя правило сложения Р, имеем P(B)=P(A)+P(B/A), откуда следует нер-во P(A) ≤ P(B)
14. условная Р  , его статистическую интерпретация? примеры, когда: 1) Р(А/В)>Р(А); 2) Р(А/В)<Р(А);
, его статистическую интерпретация? примеры, когда: 1) Р(А/В)>Р(А); 2) Р(А/В)<Р(А);
Пусть А и В случ соб по отношению к какому-либо опыту причем P(B) неравно 0. число РB(А)=Р(АВ)/Р(В)- Р соб А при условии что соб В уже наступило или просто условной Р А. Наличие условной Р (РB(А)≠Р(А)) между соб определяет их взаимосвязь. Статистич интерпретация: Рассмотрим некий эксперимент и соб. А и В. Пусть  - число опытов, в которых произойдет соб А при условии что В тоже произойдет. 1) РB(А)>Р(А) бросаем кость, В- выпало четное, А-выпала двойка. Р(А)=1/6 РB(А)=1/3. 2) РB(А)<Р(А) в коробке лежит 3 белых и 3 черных шара вытащили 1 шар, А – вытащить черный шар, В- из коробки предварительно вынули шар оказавшийся черным. Р(А)=1/2 РB(А)=2/5
- число опытов, в которых произойдет соб А при условии что В тоже произойдет. 1) РB(А)>Р(А) бросаем кость, В- выпало четное, А-выпала двойка. Р(А)=1/6 РB(А)=1/3. 2) РB(А)<Р(А) в коробке лежит 3 белых и 3 черных шара вытащили 1 шар, А – вытащить черный шар, В- из коробки предварительно вынули шар оказавшийся черным. Р(А)=1/2 РB(А)=2/5
|
|
|


