Главная | Обратная связь | Поможем написать вашу работу!

Может ли мат ожидание ДСВ, принимающей целые значения, быть числом не целым?

Мат ожиданиеДСВ, принимающей целые значения, может быть числом нецелым. Например, найдём мат ожидание числа очков, выпадающих при бросании кости, обозначим указанную СВ через X, принимающий целые значения (1; 2; 3; 4; 5; 6). Её закон распределения имеет вид:

X
P	1/6	1/6	1/6	1/6	1/6	1/6

55. Пусть X – ДСВ, принимающая только неотрицат значения и имеющая мат ожидание m. Докажите, что P (X ≥ 5) ≤ m/ 5.

Докажем нер-во Маркова: Если x>0 и a=const, a>0, то . Док-во: Введём новую величину:

Y		a
P	P(x<a)	P(x a)

X Y. M(x) M(y), M(y)= aP(X a). aP(X a) M(x). P(X a) .В нашем примере a=5 (т.е. a=const), a>0, M(x)=m. По нер-ву Маркова: P(X 5)

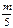
56. Докажите, что если X и Y – независ ДСВ, принимающие конечное мн-во значений, то M(XY)=M(X)M(Y) Если СВ X и Y независ, то мат ожидание их произведения = произведению их мат ожиданий (теорема умножения мат ожиданий). Возможные значения X обозначим x₁, x_2,…, возможные значения Y - y₁, y_2,… а p_ij=P(X=x_i, Y=y_j). Закон распределения величины XY будет выражаться табл. А M(XY)= Ввиду независ величин X и Y имеем: P(X= x_i, Y=y_j)= P(X=x_i) P(Y=y_j). Обозначив P(X=x_i)=r_i, P(Y=y_j)=s_j, перепишем данное равенство в виде p_ij=r_is_j_. Таким образом, M(XY) = 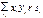= 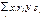. Преобразуя полученное рав-во, выводим: M(XY)=()() = M(X)M(Y)

57. Докажите, что если X и Y –ДСВ, принимающие конечное мн-во значений, то M (X + Y) = M (X) + M (Y).

Мат ожидание суммы двух СВ = сумме мат ожиданий слагаемых:M(X+Y)= M(X)+M(Y). Док-во. Пусть СВ X и Y заданы законами распределения(*):

X x₁x₂ p p₁p₂

Y y₁y₂ g g₁g₂

Составим все возможн значения величины X+Y. Для этого к каждому возможн значению X прибавим возможн значение Y; получим x₁+y₁, x₁+y₂, x₂+y₁, x₂+y₂. Предположим, что эти возможн значения различны(если не так, то док-во аналогично), и обозначим их Р соответств через p₁₁,p₁₂,p₂₁,p_22.Мат ожидание величины X+Y = сумме произведений возможн значений на их Р: M(X+Y) = (x₁+y₁)* *p₁₁+(x₁+y₂)* p₁₂+(x₂+y₁)* p₂₁+(x₂+y₂)* p₂₂, или M(X+Y) = x₁*(p₁₁+p₁₂)+ x₂*(p₂₁+p₂₂)+ +y₁*(p₁₁+p₂₁)+ y₁*(p₁₂+p₂₂). Докажем, что p₁₁+p₁₂=p₁. Соб, состоящие в том, что X примет значение x₁ (Р этого соб = p₁), влечет за собой соб, которое состоит в том, что X+Y примет значение x₁+y₁или x₁+y₂(Р этого соб по теореме сложения равна p₁₁+p₁₂), и обратно. Отсюда следует, что p₁₁+p₁₂=p_1. Аналогично доказываются рав-ва p₂₁+p₂₂=p₂, p₁₁+p₂₁=g₁и p₁₂+p₂₂=g_2.Подставляя правые части этих равенств в соотношение (*), получим M(X+Y)=(x₁p₁+x₂p₂)+(y₁g₁+y₂g₂), или M(X+Y)= M(X)+M(Y).

58. Как определяется и что хар-ует дисперсия ДСВ X? св-ва дисперсии.

На практике часто требуется оценить рассеяние возможн значений СВ вокруг ее среднего значения. Поэтому вычисляют среднее значение квадратаотклонения, которое и называется дисперсией. Дисперсией(рассеянием) ДСВ называют мат ожидание квадрата отклонения СВ от ее мат ожидания: D(X)=M[X-M(X)]². Более удобная формула: D (X) = M (X ²) − M ²(X). Св-ва: Дисперсия постоян величины С равна нулю: D (С) = 0; Постоян множитель можно выносить за знак дисперсии, возводя его в квадрат:

D(CX)=С²D(X); Дисперсия суммы двух независ СВ = сумме дисперсий этих величин: D(X + Y)= D(X)+D(Y); Дисперсия разности двух независ СВ = сумме их дисперсий: D(X-Y)=D(X)+D(Y); Прибавление(вычитание) константы к СВ не меняет ее дисперсии. D(X+C)=D(X).

59. Докажите, что если X –ДСВ, то D (X) = M (X ²) − M ²(X).

Док-во: Мат ожидание M(X) есть постоян величина ⇒ 2M(X) и M²(X) также постоян величины. D(X) = M(X ²) −M²(X)= M[X-M(X)]²=M[X²-2XM(X)+M²(X)]=M(X²)-2M(X)M(X)+M²(X)=M(X²)-2M²(X)+M²(X)=M(X²)-M²(X). т.е. D(X) = M(X ²) −M²(X).

60. Пусть X – ДСВ. Может ли выполняться нер-во M (X 2)<(M (X))²?

По определению дисперсии D(X)=M[X-M(X)]²,тогда D(X)=M[X ² -2ХM(X)+ M ² (X)]= M(X ²)-2 M ² (X)+ M ² (X)= M(X ²)- M ² (X). Итак, для любой с.в.Х D(X)= M(X ² )- M ² (X), D(X)≥0, поэтому для любой с.в. Х всегда выполняется нер-во M(X ²) ≥M ² (X). Поэтому нер-во М(Х²)< [M(X)]²выполняться не может.

61. Докажите, что если X и Y – независ СВ, то D [ XY ]= D [ X ]⋅ D [ Y ]+ M [ X ]² D [ Y ]+ M [ Y ]² D [ X ]. D(XY) = (M(XY)²)-[M(XY)]² = M(X²Y²)-(M(x))²(M(Y))² = M(X²)M(Y²)-M²(X)M²(Y) = (D(X)+[M(X)]²)(D(Y)+[M(Y)]²) – M²(X)M²(Y) = (X)D(Y)+M(Y)²D(X)+M(X)²D(Y).

62. Пусть Х –ДСВ, распределенная по бином закону распределения с параметрами n и р. Докажите, что М(Х)=nр, D(Х)=nр(1-р).

Пусть производится n независ испытаний, в каждом из которых может появиться соб А с р, так что Р противополож соб Ā равна q=1-p. Рассмотрим СВ Х – число появления соб А в n опытах. Представим Х в виде суммы индикаторов соб А для каждого испытания: Х=Х₁+Х₂+…+Х_n. докажем, что М(Х_i)=р, D(Х_i)=np. Для этого рассмотрим закон распределения СВ:

Х
Р	р	q

Очевидно, что М(Х)=р, СВ Х² имеет тот же закон распределения, поэтому D(Х)=М(Х²)-М²(Х)=р-р²=р(1-р)=рq. ⇒ М(Х_i)=р, D(Х_i)=pq. По теореме сложения мат ожиданий М(Х)=М(Х₁)+..+М(Х_n)=nр, D(Х)=D(Х₁)+…+D(Х_n)=npq=np(1-р).

63. Докажите, что для бином закона распределения СВ с Р успеха р в каждом из n независ испытаний выполняется рав-во:. =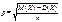

64. Пусть X –ДСВ, распределенная по закону Пуассона с параметром. Докажите, что M (X) = D (X) = λ.

Закон Пуассона задается табл:

X					…
P	λ−e	λλ−e	λλ−e!22	λλ−e!33	…

Отсюда имеем: = . Таким образом, параметр λ, хар-ющий данное пуассоновское распределение, есть не что иное как мат ожидание величины X. Это легко понять, если вспомнить, что формулы Пуассона получились как предельный вариант формул Бернулли, причем ∞→n∞→nλ = np. Поскольку для бином закона мат ожидание равно np, то неудивительно, что для пуассоновского закона M(X) = . Более того, мы можем предположить, что дисперсия X тоже будет равна λ, поскольку для бином закона D(X) = npq и 1 при →q. Действительно, непосредств подсчет дисперсии подтверждает это предположение. для закона Пуассона M(X) = λ, D(X) = λ

65. Пусть Х –ДСВ, распределенная по геометрич закону с параметром р. Докажите, что M (X) = .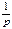

Геометрич закон связан с последовательностью испытания Бернулли до 1-го успешного А соб, р=р(А)

х			…	n	…
Р	р	pq	…	Pq^n-1	…

66. Пусть Х –ДСВ, распределенная по геометрич закону с параметром р. Докажите, что D (X) = .

67.Как определяется Cov(X,Y) СВ X,Y?Докажите, что D(X+Y)=D(X)+D(Y)+2Cov(X,Y).

COV(X,Y) СВ X,Y-мат ожидание произведения отклонений X и Y. Сov(X,Y)=M[(X-M(X)][Y-M(Y)]. Пусть Х и У–две СВ. Положим, Z=X+Y По теореме сложения мат ожиданий имеем: М(Z)=M(X)+M(Y). Вычитая это рав-во из предыдущего, получим: , где обозначает отклонение величины Х. Отсюда = 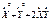. Найдем дисперсию Х+У. Имеем D(X+Y)=D(X)+D(Y)+2M(), где М() = Cov(X,Y). Формула принимает вид: D(X+Y)=D(X)+D(Y)=2Cov(X,Y)

68. св-ва Cov(X,Y) СВ Х и У. Докажите, что Cov(X,Y)=M(XY)-M(X)M(Y)

Ковариация (корреляционный момент) Cov(X, Y) СВ X, Y- мат ожидание произведения отклонений X и Y Cov(X, Y) = M [(X − M (X))(Y − M (Y))]. Св-ва: Cov(X, Y) = M (XY) − M (X) M (Y). Cov(X, X) = D (X). D (X + Y) = D (X) + D (Y) + 2Cov(X, Y). Если X и Y независимы, то Cov(X, Y) = 0. Cov(X, Y) = Cov(Y, X). Cov(aX, Y) = Cov(X, aY) = a Cov(X, Y). Cov(X + Y, Z) = Cov(X, Z) + Cov(Y, Z). Cov(X, Y + Z) = Cov(X, Y) + Cov(X, Z). Если Cov(X, Y) = 0, то СВ X и Y называются некоррелированными.

69. Как определяется коэфф корреляции ρ (X;Y) СВ X и Y? св-ва коэфф корреляции? Что можно сказать о X и Y, если ׀ ρ(X;Y) ׀ =1?

Коэфф корреляции СВ X и Y определяется формулой ρ (X;Y)= Cov(X;Y)/ (σ(X)*σ(Y)), где Cov(X;Y) – ковариация X и Y, а σ(X) – среднее квадратичное отклонение Х, σ(Y) – среднее квадратичное отклонение Y.

Основные св-ва: ρ(X;Y)=ρ(Y;X). ρ(X;Y) ׀ <=1. ׀ρ(X;Y) ׀ =1 равнозначно существованию констант a,b таких, что равенство Y=a+bX выполняется с Р 1.

70. Докажите, что коэфф корреляции 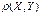СВ Х и У удовлетворяет условию . Что можно сказать о Х и У, если ? Если ?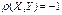

Определение. Коэфф корреляции двух СВ-отношение их ковариации к произведению средних квадратич отклонений этих величин: p_xy = K_xy /«сигма» _х «сигма» _х. Из определения следует, что р_ху = р_ух = р. Очевидно также, что коэфф корреляции-безразмерная величина. Отметим св-ва коэфф корреляции. Коэфф корреляции принимает значения на отрезке [-1;1],т.е. -1< р <1.Из нер-ва . Если коэфф корреляции двух СВ =(по абсолютной величине) 1, то между этими СВ существует линейная функциональная зависимость:

71. Чему равен ρ(X,Y) и Cov(X,Y) при условии независ СВ X, Y? Что можно сказать о ρ(X, Y), если Y=a+bX, где a и b – некоторые числа (b≠0)?

Если X и Y независ СВ, то Cov(X, Y) = M(X,Y) – M(X)M(Y) = M(X)M(Y) - M(X)M(Y) = 0. .Если (β≠0), то . Док-во: Cov(X,Y) = Cov(X, α + βX) = M (X(α+βX)) – M(X)M(α+βX) = M(Xα+βX²) - M(X)(M(α) + M(βX)) = M(Xα) + M(βX²) – αM(X) – β(M(X))²= β(M(X²) – (M(X))²)= βD(X). 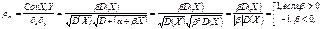т.е.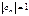

72. непрерывн СВ X. Чему в этом случае = P(X=a), где а – опред число? Следует ли из рав-ва P(X=a)=0 для непрерывн СВ X, что соб X=a никогда не наступает? СВ X называется непрерывной, если её функция распределения F(X) непрерывна в любой точке X. P(X=a), где а – опред число, есть Р каждого и отдельного знач. P(X=a)=0, т.е. Р каждого отдельного знач =0. Однако это не означает, что соб Х=а невозможно. В результате испытания СВ примет одно из возможн знач; это значение может оказаться = а.

⇐ Предыдущая 1 2 3 456 Следующая ⇒

Воспользуйтесь поиском по сайту: