 |
В чем состоит геометрич подход к определению Р? Как находится Р попадания в заданное мн-во, если точка случайно выбирается на отрезке AB? в треугольнике ABC?
|
|
|
|
Геометрич подход заключается на предположении, что попадание каждой точки в геометрич мн-ве(
), а в какое-то подмн-во А 
. Р(А) пропорциональна мере (длин, площади и т.д.) мн-ва А, т.е. Р(А)= с 
(А)), где 
(А)- мера мн-ва А, а с=const. Т.к. P(
)=1, то с = 1/ (
), так что Р(А)= 
. 1) - АВ, F -отрезок СD, СD 
АВ. 
- длина, (CD)=d-c, 
(BA)=b-a, значит Р(А)= 
. 2) -треугольник АВС, F-фигура 
. (F) =площадь F, ()-площадь АВС. Р(F)=площадь F/ площадь ABC.
24. В чем состоит геометрич подход к определению Р? Как находится Р попадания в заданное мн-во, если точка случайно выбирается в круге радиуса r? в кубе со стороной a?
Геометрич подход заключается на предположении, что попадание каждой точки в геометрическом множестве(), а в какое-то подмножество А . Р(А) пропорциональна мере (длин, площади и т.д.) множества А, т.е. Р(А)= с 
(А), где (А) -мера множества А, а с=const. Т.к. P()=1, то с = 1/ 
(), так что Р(А)= 
. 1) - круг с радиусом r, F – фигура , (F)=площадь F, ()=площадь . P(F)=площадь F/площадь круга радиуса r. 2) P(F)=объем F/ объем круга
25. полная группа соб? пример, когда соб АВ, 
и 
не образуют полной группы соб.
Полная группа соб - система случ соб такая, что в рез-те произведённого случ эксперимента непременно произойдёт одно из них. АВ, А*В, А*+В* (чёрточка одна на А и В)-не образуют полной группы соб.
А*+В*(чёрточка одна на А и В)=А*В*. Полную группу событий составляют: АВ, А*В, АВ*, А*В*
Сл-но АВ, А*В, А*В* - не образуют полной группы. Пример: студент сдаёт 2 зачёта, соб.А- сдан 1 зачёт, соб.В- сдан 2 зачёт, Р(А)=1/2, Р(В)=2/3. Р(АВ+А*В+А*В*)≠1, т.к. Р(АВ*)≠0, сл-но соб. АВ, А*В, А*+В* (чёрточка одна на А и В)-не образуют полной группы.
26. Верно ли, что соб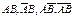 
образуют полную группу для любых соб А и В?
Да, соб 
образуют полную группу соб для любого А и В, т.к. они попарно несовмест и при каждом осуществлении опыта обязательно наступит хотя бы одно из них.
|
|
|
27 Соб A влечет соб B. Верно ли, что P(A) + P(AB) + P(B) =1?
Если в каждом из n независ испытаний Р появления A const, то как угодно близка к 1 Р того, что отклонение относит частоты от Рпо абс величине будет сколь угодно малым, если число испытаний достаточно велико. 
xi-число появлений соб в i-м испытании (i=1…n). Каждая из величин может принимать 2 значения: 1 с вер-ю р, 0 с вер q. xi- попарно независ., тогда D(xi)=pq. Т.к. p+q=1, то pq 
1/4 
дисперсии огранич с=1/4. Применим т. Чебышева, получим 
. Мат ожидание а каждой из величин xi = р наступл. событ. 
. Каждая xi при появлении соб в соотв. испытании принимает значение = 1 
x1+x2+…+xn= m появлен. события в n испытаниях 
(x1+x2+…+xn)/n= m/n. Учитывая это, получим, 
28. Сформулируйте и докажите формулу полной Р. пример применения. Следствие теорем–сложения Р и умножения Р–формула полной вероятности. Пусть Н1, Н2-полная группа соб. Тогда Р любого соб А может быть вычислена: 
Док-во: т.к. гипотезы Н1, Н2,..Нn образуют полную группу, то соб А может появиться только в комбинации с какой-либо из этих гипотез: 
. Т.к. гипотезы Н1, Н2,..Нn несовмест, то и комбинации 
также несовмест; применяя к ним теорему сложения, получим: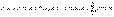 
. Применяя к соб 
теорему умножения, получим: 
. Пример. Имеются 3 одинак урны с шарами. В 1 из них находится 3 бел и 4 черн, во 2-2 бел и 5 чёрн, а в 3-10 чёрн шаров. Из случ выбранной урны наудачу вынут шар. С какой Р он окажется бел? Будем считать соб Н1,Н2,Н3 выбором урны с соотвеств номером, а соб А-выбором бел шара. По условию все соб выбора урны равновероятны, значит: 
.найдём Р события А при выборе каждой урны: 
получаем 
29. Сформулируйте и докажите формулу Байеса. пример применения. Пусть Н1,Н2,..Нn-полная группа соб, и А — некоторое соб, Р кот положит. Тогда условная Р того, что имело место событие Нk, если в результате эксперимента наблюдалось соб А, может быть вычислена: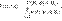 
Док-во: Формула Байеса вытекает из определения условной Р. Р совмест соб АВ двояко выражается через условные Р 
. Þ 
. Пример. Соб A-в баке нет бензина, соб B-машина не заводится. Заметим, что вероятность P(B|A) того, что машина не заведется, если в баке нет бензина,=1. Тем самым, P(A) того, что в баке нет бензина,=произведению P(B) того, что машина не заводится, на P(A|B) того, что причиной соб B стало именно отсутствие бензина (A), а не, к примеру, разряженный аккумулятор.
|
|
|
30. схема Бернулли?формул 
для Р k успехов в серии n испытаний по схеме Бернулли, пример применения. Схема Бернулли: производится n независ испытаний, в каждом из которых с одной и той же p наступает некоторое соб А (успехом) и, следовательно, с q=1-p наступает соб 
, противопол А. Пусть k – любое из чисел 0,1,2,…, n. Обозначим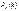 
Р того, что в n испытаниях Бернулли успехов наступит k раз. Справедлива формула Бернулли: 
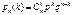. Пример: Монета бросается 10 раз. Какова Р того, что герб выпадает при этом ровно 3 раза? В данном случае успехом считается выпадение герба, p этого события в каждом опыте равна ½, так что q=1-p=1|2. Отсюда 
.
31. Выведите формулу 
для вероятности k успехов в серии n испытаний по схеме Бернулли.
Когда производится n одинак и независ опытов, каждый из которых имеет 2 исхода { A; 
}. Т.е. некоторый опыт повторяется n раз, причем в каждом опыте некоторое событие А может появиться с P(A)=q или не появиться с P(
)=q-1=p. Пространство элемент соб каждой серии испытаний содержит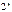 
точек или последовательностей из символов А и 
. Такое вероятностное пространство-схема Бернулли. Задача:для данного k найти Р того, что при n- кратном повторении опыта соб А наступит k раз. каждое наступление соб А рассматриваем как успех, ненаступление А – как неуспех. цель – найти Р того, что из n опытов ровно k окажутся успешными; обозначим это соб через B. Соб В представляется в виде суммы ряда соб-вариантов соб В. Чтобы фиксировать опред вариант, нужно указать номера тех опытов, которые оканчиваются успехом. Например, один из возможных вариантов есть 
. Число всех вариантов равно 
, а Р каждого варианта ввиду независимости опытов равна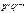 
. Отсюда Р события В равна 
. Чтобы подчеркнуть зависимость полученного выражения от n и k, обозначим его 
. Итак, 
.
32. Выведите формулу для дисперсии выборочной средней бесповторной выборки. Выборочная дисперсия Db- среднее арифметическое квадрата отклонения наблюдаемого значения признака от их среднего значения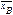 
. Если все значения х1+х2+…+хn выборки v n различны, то DB= 
.Если значения признака х1,х2,…хn имеют с оответств частоты n1,…nk; n1+…+nk=n, то 
. D= 
. 
= 
|
|
|
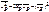33. Пусть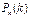 
- Р k успехов в серии n независ испытаний с Р успеха p в каждом испытании. При каком k 
достигает макс? Совпадает ли это число с мат ожиданием кол-ва успехов? Чему равна сумма 
?
Рассмотрим два соседних числа 
и 
. М ежду ними имеет место одно из соотношений: 
(<, = или >) или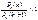 
. Подставляя вместо числителя и знаменателя их выражения по формулам 
, 
или учитывая, что 
, получим соотношения 
или 
. Собирая все слагаемые с множителем k и учитывая, что p+q=1, получим эквивалент соотношения 
. Обозначим число np+p через 
. Тогда: 
. Таким образом, для всех значений k меньших чем 
справедливо нер-во 
, для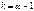 
(это возможно только в том случае, когда 
- целое число) имеет место рав-во 
, наконец, при 
выполняется нер-во 
. Тем самым при значениях 
функция возрастает, а при значениях 
убывает. Следоват, если число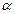 
не является целым, то ф-ция имеет единств макс; он достигается при ближайшем к 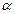слева целом значении k, т.е. при таком целом 
, которое заключено между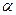 
-1 и 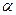: np-q< 
<np+p, =[np+p]. Если же 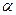- целое число, то два равных между собой макс достигается при 
и 
. Если число 
не целое, то наиб вероятное число успехов равно ближайшему к 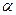слева целому числу. В случае когда 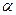есть целое число, наиболее вероятное число успехов имеет два значения: 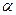-1 и .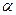
|
|
|
