 |
Соответствие между моделью и действительностью: сходство
|
|
|
|
В предыдущем параграфе мы обсуждали соответствие между моделью и оригиналом с позиций различия между ними. Рассмотрим теперь более трудный вопрос – о сходстве между ними. Поскольку различия между моделью и реальностью принципиально неизбежны и неустранимы, существует предел истинности, правильности наших знаний, сконцентрированных в моделях. Является ли этот предел вечным, принципиально неотодвигаемым или имеется возможность неограниченно увеличивать сходство наших моделей с реальностью? Или, говоря философским языком, доступна ли объективная истина субъективному познанию?
Различные философские учения отвечали на этот вопрос по-разному. Субъективные идеалисты вообще отрицали наличие какой-либо реальности вне сознания субъекта либо считали ее продуктом сознания. Античные софисты считали и саму реальность, и всякое знание о внешней реальности относительными, субъективными и индивидуальными; разные мнения об одном, принадлежащие разным субъектам, считались одинаково истинными (“что кому как является, так оно и есть для того, кому является”). Агностики признавали ощущения единственной реальностью и потому считали, что познанию доступны лишь явления, а сущности и закономерности реального мира принципиально непознаваемы. Диалектический материализм освещает этот вопрос в плане отношений между относительной истиной, т.е. объективным, но не полным содержанием сегодняшнего человеческого познания, и истиной абсолютной: истина относительная может пополняться, развиваться, приближаясь к истине абсолютной, и принципиального предела этому приближению не существует. Степень правильности относительных истин, наличие в моделях элементов, не обладающих истинностью, обнаруживаются в практике человеческого общества.
|
|
|
ИСТИННОСТЬ МОДЕЛЕЙ
Весь исторический опыт науки, техники, общественной практики подтверждает верность диалектико-материалистической теории познания. Например, в современной теории тепловых процессов многое сохранилось со времен С. Карно, но от модели теплорода как особой субстанции – носителя тепла пришлось отказаться; в основе современной электродинамики лежат уравнения Максвелла, но от механической максвелловской модели эфира до современных представлений о физическом вакууме – огромная дистанция [12].
Рассмотрение проблемы истинности знаний с философских позиций требует глубокого и всестороннего анализа многих аспектов даже на примере одной науки (так, о физике см. [21]). Наша задача гораздо конкретнее: обратить внимание на сочетание истинного и предполагаемого (могущего быть как верным, так и неправильным) во всех моделях.
Еще раз подчеркнем, что об истинности, правильности или ложности модели самой по себе говорить бессмысленно: только в практическом соотнесении модели с отображаемой ею натурой выявляется степень истинности. При этом изменение условий, в которых ведется сравнение, весьма существенно влияет на его результат: именно из-за этого возможно существование двух противоречивых, но “одинаково” истинных моделей одного объекта. Яркий пример этого – волновая и корпускулярная модели света или электрона; эти модели различны, противоположны и истинны, каждая в своих условиях. Важно отметить, что каждая модель явно или неявно содержит условия своей истинности, и одна из опасностей практики моделирования состоит в применении модели без проверки выполнения этих условий. В инженерной практике такая ситуация встречается чаще, чем принято думать. Например, для определения пропускной способности различных каналов связи нередко используют формулу Шэннона – Таллера, хотя она верна только для конкретных (гауссовых) каналов. Для обработки экспериментальных данных часто употребляют статистические процедуры, не проверяя условий их применимости (скажем, нормальности или независимости). Иногда это делается вынужденно (не всякое условие бывает возможным проверить), но тогда и к полученным результатам должно быть осторожное, условное отношение, что, к сожалению, не всегда имеет место. Такие ситуации выдвинули перед исследователями специальную проблему – создание моделей, применимость которых сохраняется в некотором диапазоне условий; например, в математической статистике этому соответствуют непараметрические и робастные процедуры обработки данных в теории управления и прикладной математике – исследование устойчивости моделей и регуляризация алгоритмов и т. п.
|
|
|
| TRUE, CORRECT, PROPERистинный FALSE, ERRONEOUSложный CAUSE, REASON, MOTIVE причина CORRESPONDENCE, ACCORDANCEсоответствие EVOLUTIONэволюция Реальные модели служат заместителями оригинала благодаря своему подобию с ним. Возможны три вида подобия: прямое (устанавливаемое через физическое взаимодействие), косвенное (устанавливаемое через аналогию, т.е. через общую абстрактную модель) и условное (устанавливаемое через соглашение). В каждой модели есть доля истины, т.е. в чем-то любая модель правильно отражает оригинал. Степень истинности модели проявляется при практическом соотнесении модели и оригинала (“практика – критерий истинности”). Кроме безусловно истинного, в модели есть и верное лишь при определенных условиях и нечто “не-верное”, т.е. не имеющее отношения к оригиналу. |
СОЧЕТАНИЕ ИСТИННОГО И ЛОЖНОГО В МОДЕЛИ
Еще один важный аспект соотношения истинного (т.е. определенно известного и правильного) с предполагаемым (т.е. возможным, но не обязательно действительным) при построении моделей состоит в том, что ошибки в предположениях имеют разные последствия для прагматических и познавательных целей. Если ошибки в предположениях вредны и даже губительны при использовании прагматических моделей, то при создании познавательных моделей поисковые предположения, истинность которых еще предстоит проверить, – единственный способ оторваться от фактов. Роль гипотез в науке настолько важна, что образно можно сказать, что вся научная работа состоит в выдвижении и проверке гипотез. А. Эйнштейн писал:
|
|
|
“Воображение важнее знания, ибо знание ограничено. Воображение же охватывает все на свете, стимулирует прогресс и является источником его эволюции”.
Среди других аспектов проблемы правильности моделей, истинности знаний для целей системного анализа важен аспект явной рефлексии уровня истинности: что известно точно, достоверно; что – с оцениваемой степенью неопределенности (например, с известной вероятностью для стохастических моделей или с известной функцией принадлежности для расплывчатого описания); что – с неопределенностью, не поддающейся оценке; что может считаться достоверным только при выполнении определенных условий; наконец – что известно о том, что неизвестно.
| Подведем итог Главная ценность моделей как формы знаний состоит в том, что они содержат объективную истину, т.е. в чем-то правильно отображают моделируемое. Однако кроме безусловно истинного содержания в модели имеется и условно-истинное (т.е. верное лишь при определенных условиях), и предположительно-истин-ное (т.е. условно-истинное при неизвестных условиях), а следовательно, и ложное. При этом в каждых конкретных условиях неизвестно точно, каково же фактическое соотношение истинного и ложного в данной модели. Ответ на этот вопрос дает только практика. Однако в любом случае модель принципиально беднее оригинала, это ее фундаментальное свойство. | Summary The main virtue of models as a representation of knowledge is that they contain an objective truth; i.e., they correctly represent modeled objects in certain respects. But besides a definitely correct content, each model contains a conditionally correct (i.e., true only under certain conditions) and a wrong content. In any given circumstance the real proportions between correct and erroneous content in a given model are not fully known. Only practice can give an answer to this. But in any case a model is principally poorer than the original; this is its funda-mental property. |
О ДИНАМИКЕ МОДЕЛЕЙ
Как и все в мире, модели проходят свой жизненный цикл: они возникают, развиваются, сотрудничают или соперничают с другими моделями, уступают место более совершенным. Одни модели живут дольше отдельных людей, и тогда этапы жизненного цикла моделей изучаются в виде истории той или иной отрасли знаний или деятельности (например, истории физики, истории авиации, истории гончарного искусства и т.д.). Жизненный цикл других моделей должен быть обязательно завершен в обозримый срок, и тогда перевод модели от этапа к этапу становится технологическим действием, должен выполняться как можно эффективнее (быстрее, лучше, дешевле). Как мы уже знаем, это невозможно без моделирования самого процесса моделирования, т.е. алгоритмизации моделирования.
|
|
|
Наиболее полно необходимость алгоритмизации моделирования осознана там, где проблема эффективности действия стоит особенно остро: в проектной деятельности [5], в исследовании операций [3], в изобретательском поиске [2], в создании АСУ [14], в имитационном моделировании [22].
Остановимся на важнейших причинах и закономерностях динамики моделей. Прежде всего очевидно, что процесс моделирования структурирован, организован, состоит из последовательности этапов. Этапы отличаются качественно, конкретными целями и средствами и должны выполняться в определенной очередности. Например, при конструировании новой технической системы ее модель развивается от воплощения в виде результатов предыдущей научно-исследовательской работы по стадиям технического задания, технического проекта, рабочего проекта, опытного образца, мелкой серии до модели, предназначенной для промышленного выпуска. Другой пример дают рекомендации по последовательности этапов имитационного моделирования: формирование целей моделирования – построение абстрактной модели – создание имитационной реальной модели – ее исследование – обработка и интерпретация результатов.
СЛОЖНОСТИ АЛГОРИТМИЗАЦИИ МОДЕЛИРОВАНИЯ
Стремление к совершенству требует алгоритмизации, и для многих исследователей исходным стремлением было найти наиболее эффективную последовательность этапов в работе с моделями. Однако здесь обнаружилось, что в практике моделирования чаще всего не удается строго выдержать рекомендуемую последовательность действий. Более того, стало очевидным, что вообще не существует какого-то единого, пригодного для всех случаев алгоритма работы с моделями. Это вызвано разными причинами.
Во-первых, как мы знаем (см. § 2.4), модель функционирует в культурной среде, и конкретное окружение каждой модели может настолько отличаться, что опыт работы с одной моделью не может без изменений переноситься на другую.
|
|
|
Во-вторых, требования, предъявляемые к модели, противоречивы: полнота модели противоречит ее простоте, точность модели – ее размерности, эффективность – затратам на реализацию. Многое в истории данной модели зависит от того, какой именно компромисс выбран между этими противоречащими критериями.
В-третьих, с самого начала невозможно предусмотреть все детали того, что произойдет в будущем с любой моделью. Моделирование призвано устранить неопределенность, но существует неопределенность и в том, что именно надо устранять. Начальные цели впоследствии могут оказываться неполными. Например, по результатам испытаний опытного образца часто приходится вносить изменения в техническое задание и снова возвращаться к этапам проектирования образца. Приведем другой пример: после интерпретации результатов имитационного моделирования цели уточняются, в модель вносятся изменения и моделирование повторяется. Недостатки модели проще и легче обнаружить и исправить в ходе моделирования, чем предусмотреть их заранее. Это еще одна причина динамичности моделей.
Однако среди всех причин невозможности полной алгоритмизации процесса моделирования особо выделяются еще две, последние по счету, но не по важности. Они различаются тем, насколько большой вес придается роли отдельного человека в развитии модели.
Желая выявить алгоритм моделирования, естественно обратиться к инженерной и научной практике: ведь именно в этих видах деятельности наиболее сильно выражено стремление к формализации, точности, определенности. Появляется надежда на обнаружение закономерностей моделирования при наблюдении работы инженеров и ученых над созданием моделей. Оказалось, что даже в этой области
“любой набор правил для разработки моделей в лучшем случае имеет ограниченную полезность и может служить лишь предположительно в качестве каркаса будущей модели или отправного пункта в ее построении” [22, с. 33].
Более того, даже в чистой математике разработка моделей невозможна без эвристического, творческого, неформального начала [1]. К. Жаблон и К. Симон анализируют эту ситуацию следующим образом:
“Как же тогда можно убедиться, что та или иная реальная задача может быть простым способом смоделирована? Только если найдена простая модель! Этот ответ не шутка. Теория разрешимости Геделя и Клини дает такой результат: не существует универсальной программы, которая при рассмотрении реальной задачи могла бы решить, существует ли подходящая модель, и которая могла бы ее построить” [6].
Обсуждение вопроса о соотношении формальных и эвристических приемов в процессе построения моделей завершим словами Р. Шэннона:
“Искусством моделирования могут овладеть те, кто обладает оригинальным мышлением, изобретательностью и находчивостью, равно как и глубокими знаниями систем и физических явлений, которые необходимо моделировать. Не существует твердых и эффективных правил относительно того, как надо формулировать задачу в самом начале процесса моделирования, т.е. сразу же после первого знакомства с ней. Не существует и магических формул для решения при построении модели таких вопросов, как выбор переменных, и параметров, соотношений, описывающих поведение системы, и ограничений, а также критериев оценки эффективности модели. Помните, что никто не решает задачу в чистом виде, каждый оперирует с моделью, которую он построил, исходя из поставленной задачи. Все эти соображения должны помочь читателю правильно разобраться в особенностях моделей и в некоторых вопросах искусства моделирования” [22, с. 35].
Итак, говоря о том, как отдельные люди осуществляют построение моделей, мы должны признать, что в этом процессе кроме осознанных формализованных, технических и научных приемов огромную, решающую роль играет то, что мы называем творчеством, интуитивным искусством. В этом одна из главных причин невозможности полной формализации процесса моделирования.
ЕСТЕСТВЕННАЯ ЭВОЛЮЦИЯ МОДЕЛЕЙ
Еще с одним аспектом этой невозможности мы сталкиваемся тогда, когда моделирование осуществляется не отдельным индивидуумом, а коллективно, не осознанно, а как бы стихийно, естественным эволюционным путем. Проявлением такого способа моделирования является фольклор. Другие примеры дают мозговой штурм и синектика (о которых мы еще будем говорить в § 9.6 как о методах коллективного системного анализа). Естественное развитие моделей происходит не только у людей. Интересный пример этого наблюдали орнитологи. В некоторых европейских странах принято доставлять молоко заказчикам, расставляя по утрам бутылки прямо у дверей или калиток домов. Было замечено, что в одном районе большого города синицы научились пробивать клювом сделанные из фольги крышечки бутылок и отпивать молоко. Вскоре это умение синиц распространилось на весь город и за его пределы.
Это явление развития модели “естественным путем”, как бы “самостоятельной жизни” модели в подходящей культурной среде, наблюдается не только в действительно естественных условиях (скажем, в языковой практике – слухи и анекдоты), но и в более специфических условиях инженерной практики. Например, в имитационном моделировании все чаще начинают с реализации самой простой модели самой сложной ситуации (минимаксный подход), а затем ее усложняют и отрабатывают. В проектировании технических систем все чаще отступают от традиционного надежного, но длительного пути “НИР – ОКР – производство” и прибегают к созданию реальной, пусть плохой, но действующей системы-макета, а затем ее “доводят”, постепенно улучшая. Пожалуй, наиболее ярко это проявляется сейчас в разработке систем программного обеспечения ЭВМ. Однако эволюционное развитие научно-технических моделей происходит не только тогда, когда мы “организуем” его, но и независимо от нашего желания. Эту тенденцию на примере истории техники очень последовательно проследил С. Лем [8].
Итак, еще один путь неформализуемого развития модели – это ее эволюционная динамика в среде, которой она ингерентна (см. § 2.4).
| Подведем итог Основные положения данного параграфа заключаются в следующем: как и любые реальности, модели также претерпевают изменения, проходят свой “жизненный цикл”; пользование готовыми моделями обычно не требует знания их истории, но знание закономерностей развития моделей полезно и необходимо разработчикам; на этапе построения моделей решающую роль играют неформализуемые эвристические способности человеческого интеллекта; существует эволюционный тип развития моделей, при котором вклад отдельных личностей мал, случаен, но в целом приводит к прогрессу модели; неформализуемость основных этапов построения модели, превращающая этот вид деятельности в искусство, не означает, что наука вообще и алгоритмизация в частности непричастны к этому, что нельзя дать никаких полезных и конкретных рекомендаций, повышающих эффективность моделирования; наука моделирования состоит в разделении процесса моделирования на этапы (см., например, [20]), детальном изучении каждого этапа и его описания с максимально возможной степенью формализации, рассмотрения и оценивания вариантов; в целом моделирование является неразделимым сочетанием, сплавом науки и искусства. | Summary The main principles set forth in this section are as followes: – Like all of reality, models are subject to change; they possess a life cycle. – One does not need to know the history of a model in order to use it; but a knowledge of the general laws governing model development is useful and even necessary for designers of models. – In model design a decisive role is played by the nonformalizable heuristic capacities of human intelligence. – There is also an evolutionary mode of model development, in which progress is made by small and random contributions of many people involved. – The fact that many important stages of modeling are nonformalizable makes modeling activity an art; but this does not mean that science and algorithmization have nothing to do with modeling, that useful, concrete recommendations and methods facilitating modeling cannot be given. – The science of modeling encompasses the division of modeling into stages (cf., for example [20]), the detailed study of each stage with as formalized a description as possible, and the consideration and assessment of alternative models. – The process of modeling is an inseparable fusion of science, craft and art. |
ЗАКЛЮЧЕНИЕ
Обратим внимание на то, что понятие модели оказалось невозможным ограничить только тем самым, что мы непосредственно называем моделью. Если мы хотим включить в это понятие все существенное, т.е. учесть наиболее общие, важные свойства модели и основные условия проявления этих свойств, то мы вынуждены рассматривать все взаимодействия между всеми “сторонами-участниками” моделирования. Таких “участников”, в самом укрупненном представлении, четыре (рис. 2.2): “субъект” – инициатор моделирования и/или пользователь его результатов; “объект-оригинал” – предмет моделирования; “модель” – отображение объекта; “культура” – среда, в которой находятся и с которой взаимодействуют все остальные “участники”.
Все сказанное в предыдущем абзаце и изображенное на рис. 2.2 является моделью модели.
Для удобства приведем схему построения рассуждений главы в целом. Если в центр всех рассуждений поставить саму модель – концентратор нужной имеющейся информации об объекте-оригинале (а ведь для каких-то целей можно сделать иначе – мы теперь знаем, что всякая модель, в том числе и модель модели, является целевой), то общая схема данной главы может быть проиллюстрирована рис. 2.3.
Если же акцент переместить с того, что такое модель, на то, как она функционирует, то следует отметить один из многих аспектов этого вопроса, а именно: иерархическую организованность моделей, их разноуровневость, включенность одних в другие. Такая организация мира моделей имеет множество важных последствий, которые мы упоминали в разной степени; наиболее важные из них – соответствие модельных построений и отображаемых ими структур природы (см. гл. 1) и ингерентность моделей (см. § 2.4). Сейчас же стоит обратить внимание на то, что иерархический способ построения модели позволяет ей успешно функционировать при различной подробности, детализации, продвинутости, формализованности ее составляющих частей. Оказывается возможным в единой структуре направить на общую цель самые разнообразные модели – от языковых, содержательных, до математических, формальных, и даже модели, отличающиеся не только степенью формализации, но и самими языками описания. Например, в территориальных АСУ основными языками описания любой подсистемы (до уровня производственного объекта) являются языки: финансовый, производственный и социально-ценностный [15]. Эта же особенность иерархического построения модели проявляется на всех уровнях, вплоть до

2.2—————Схема, отображающая модель как многоместное отношение

2.3—————Последовательность тем, рассмотренных в гл.2
уровня математических моделей. Так, Розенблют и Винер, говоря о математических моделях, подчеркивают, что формальная модель может быть разнородной совокупностью элементов, часть из которых изучена детально, т.е. конкретно и структурно, а другая часть – только исходя из соображений ее общей работоспособности, т.е. обобщенно и функционально [18].
Известно много определений модели. Это объясняется тем, что определение также модель; разным целям требуется сопоставить разные аспекты моделей, поэтому различие в определениях модели неизбежно. Еще одна причина различия – ингерентность. Даже одинаковую мысль на разных языках приходится выражать по-разному.
Если попытаться подытожить все сказанное в данной главе в виде еще одного определения модели, то оно может выглядеть так:
Модель есть отображение: целевое; абстрактное или реальное, статическое или динамическое; ингерентное; конечное, упрощенное, приближенное; имеющее наряду с безусловно-истинным условно-истинное и ложное содержание; проявляющееся и развивающееся в процессе его создания и практического использования.
Если же это определение покажется чересчур громоздким, то его вполне можно заменить кратким эквивалентом: модель есть системное отображение оригинала. Это сокращение мы приводим не столько для определения модели, сколько для иллюстрации того, насколько богато понятие системности.
ЛИТЕРАТУРА
1. Адамар Ж. Исследование процесса изобретения в области математики. – М.: Сов. радио, 1970.
2. Альтшулер Г.С. Найти идею. – Новосибирск: Наука, 1986.
3. Дегтярев Ю.И. Исследование операций. – М.: Высш. шк., 1986.
4. Демьяненков В.З. Проблема понимания как предмет вычислительной лингвистики. – В кн.: Лингвистическое обеспечение информационных систем, – М., 1987.
5. Джонс Дж. К. Методы проектирования. – М.: Мир, 1986.
6. Жаблон К., Симон Ж.-К. Применение ЭВМ для численного моделирования в физике. – М.: Наука, 1983.
7. Кемени Дж., Снелл Дж. Кибернетическое моделирование. Некоторые приложения. – М.: Сов. радио, 1972.
8. Лем С. Сумма технологий, – М.: Мир, 1968.
9. Ленин В.И. Полн. собр. соч. Т. 29.
10. Маркс К., Энгельс Ф. Соч. 2-е изд. Т. 23.
11. Неуймин Я.Г. Модели в науке и технике. – Л.: Наука, 1984.
12. Подольный Р. Нечто по имени нечто. – М.: Знание, 1983.
13. Пойа Д. Математика и правдоподобные рассуждения. – М.: ИЛ, 1957.
14. Перегудов Ф.И. Основы системного проектирования АСУ организационными комплексами. – Томск: ТГУ, 1984.
15. Перегудов Ф.И. и др. Системное проектирование АСУ хозяйством области – М.: Статистика, 1977.
16. Рассел Б. Человеческое познание. М., 1957.
17. Растригин Л.А. Кибернетика и познание. – Рига: Зинатне, 1978.
18. Розенблют А., Винер Н. Роль моделей в науке. – В кн.: Неуймин Я.Г. Модели в науке и технике. – Л.: Наука, 1984.
19. Седов Л.И. Теория подобия и размерности в механике. – М.: ГИТТЛ, 1954.
20. Хагер Н. Этапы формирования моделей. – В сб.: Эксперимент. Модель. Теория. – М. – Берлин: Наука, 1982.
21. Чешев В.В. Проблема реальности в классической и современной физике. – Томск: ТГУ, 1984.
22. Шэннон Р. Имитационное моделирование систем – искусство и наука. – М.: Мир; 1978.
23. Штофф В.А. Моделирование и философия. – М. – Л.: Наука, 1966.
УПРАЖНЕНИЯ
§ 2.2
· Обсудите различия в моделях лошади с позиций крестьянина, жокея, кавалериста, скульптора, коневода, повара. Задача обсуждения – иллюстрация целевого характера моделей.
· В каких обстоятельствах карта местности является познавательной, а в каких – прагматической моделью?
§ 2.3
· Попробуйте рассмотреть ваше любимое стихотворение как модель. Обсудите реальные и абстрактные аспекты дорожных знаков.
· Если условное подобие определяется соглашением, то чем ограничена свобода выбора моделей условного подобия?
§ 2.4
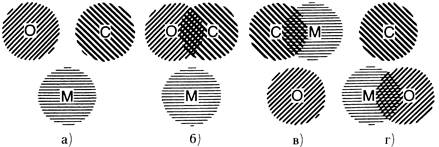
· На рис. 2.2 субъект (С), объект моделирования (О) и модель (М) изображены отдельно, что можно интерпретировать как их раздельное физическое существование. Однако могут иметь место ситуации, когда они полностью или частично совмещены (например, человек изучает свой собственный организм, скажем, измеряет себе температуру). На рис. 2.4 приведено несколько вариантов такого совмещения. Придумайте реальную ситуацию, отвечающую каждому варианту схемы моделирования.
§ 2.5
· “Я знаю, что ты знаешь, что я знаю”. Сколько ветвей и уровней в этой иерархии моделей? Попробуйте изобразить это графом.
· Экстрасенс, делая пассы руками, снимает головную боль у пациента и объясняет это взаимодействием своего биополя с биополем пациента. Обсудите соотношение адекватности и истинности модели, предложенной экстрасенсом.
· Приведите примеры конечности, упрощенности и приближенности моделей.
§ 2.6
· (Для знающих физику.) Обсудите, в каких условиях проявляются волновые свойства элементарных частиц и чем эти условия отличаются от тех, когда корпускулярная модель более адекватна.
 2.4—————Различные варианты физического совмещения отдельных компонент процесса моделирования
2.4—————Различные варианты физического совмещения отдельных компонент процесса моделирования
|
· Попробуйте в знакомой вам модели (например, в законе Ома или в описании купленной вами вещи) отыскать безусловно-истинное, условно-истинное и ложное содержание.
· Тема для обсуждения: насколько хорошо может простая модель отразить сложное явление? Аргументы в дискуссии подкрепляйте примерами. В качестве одного из таких примеров можете рассмотреть следующий (не претендующий на полную серьезность).
· “Теория счастья”. Для построения содержательной теории некоторого явления совсем не обязательно его определять; достаточно ввести его количественную меру. Например, в теории информации не рассматривается, что такое информация, а все содержание теории основано на количестве информации. В теоретической механике не обсуждается вопрос о том, что такое движение; в электродинамике – что такое электричество и магнетизм; этим теориям достаточно количественных характеристик изучаемых явлений. То же имеет место и для предлагаемой “теории счастья”. В качестве аксиом предлагаются следующие положения:
1°. Каждый индивид наблюдает окружающую его реальность (Р) и имеет свое представление о желательном состоянии реальности, т.е. идеал (И). (Это может быть идеал любого уровня – идеал вкусного обеда, любимой работы, человеческого общения, настоящего друга, справедливости и т.п.)
2°. Мерой счастливости индивида можно считать функцию, монотонно зависящую от степени совпадения Р и И: чем сильнее они различаются, тем менее счастлив индивид.
3°. Каждому индивиду присуще природное стремление к повышению своей счастливости.
Этих аксиом достаточно для вывода следующих суждений. Существуют разные способы повышения счастливости, и все из них имеют место в жизни:
а) изменяя реальность, приближать ее к идеалу (Р ® И). В зависимости от идеалов имеем спектр индивидов, идущих по этому пути – от революционеров, реформаторов, просветителей, через “рядовых” тружеников, до (к сожалению) нарушителей законов;
б) сближать реальность и идеал с помощью изменения идеала (И ® Р). Снова имеем спектр лиц, следующих такой возможности: от конформистов до циников, но в этом ряду есть и обычные люди, отказывающиеся от несбыточных идеалов;
в) подменять реальность ее иллюзией, уменьшая тем самым расхождение реальности и идеала. Здесь очевидны роль алкоголя, наркотиков; но не стоит ли в этом же ряду “массовая культура”? А “ложь во спасение”, например в отношениях между врачами и смертельно больными пациентами?
г) сохранять баланс при привитии идеалов: идеал должен быть потенциально достижимым.
§ 2.7
· Тема для обсуждения: культура как “вторая природа” (возможные аспекты дискуссии: объективные процессы в развитии культуры; роль моделей в культуре; возможны ли резкие ускорения в развитии культуры; формы взаимодействия модели с культурой и т.д.).
· В § 2.7 перечислены причины, способствующие динамике, изменчивости моделей. Приведите примеры, иллюстрирующие каждую из этих причин.
Вопросы для самопроверки
1. Что заставляет нас пользоваться моделями вместо самих моделируемых объектов?
2. Какие функции выполняют модели во всякой целесообразной деятельности? Можно ли осуществлять такую деятельность без моделирования?
3. В каком смысле модель можно назвать “окном”, сквозь которое мышление “видит” мир?
4. Каково главное отличие между познавательной и прагматической моделями?
5. Какими средствами располагает человек для построения моделей?
6. Что необходимо для перехода от моделей в терминах естественного языка к математическим моделям?
7. Что общего между моделью и оригиналом при косвенном подобии?
8. Почему знаки можно назвать материальными по форме и абстрактными по существу моделями?
9. Что такое ингерентность модели?
10. В каком смысле можно говорить о конечности моделей?
11. В чем различие между адекватностью и истинностью модели?
12. Каковы причины того, что любая модель со временем изменяется?
| Системы модели систем | Глава третья |
|
|
|


