 |
Формула средних прямоугольников
|
|
|
|
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ «МАМИ»
Кафедра «Прикладная и вычислительная математика»
имени Э.И.Григолюка
Е.А.Лопаницын
С.Г.Сальков
А.Б.Фролов
Численные методы.
расчеты в microsoft Excel 2000
ПРИ ИССЛЕДОВАНИИ АВТОМОБИЛЬНЫХ КОНСТРУКЦИЙ
Допущено УМО вузов РФ по образованию в области транспортных
машин и транспортно-технологических комплексов в качестве
учебного пособия для студентов, обучающихся по специальности
Автомобиле- и тракторостроение
МОСКВА – 2008
УДК 519.6
Рецензенты:
д.ф.- м.н., проф. Е.Б.Кузнецов (Московский авиационный институт);
д.ф.-м.н., проф. В.И.Мышенков (Московский государственный
университет леса).
Лопаницын Е.А., Сальков С.Г., Фролов А.Б. Численные методы. Расчеты в Microsoft Excel 2000 при исследовании автомобильных конструкций. Учебное пособие по дисциплине «Математика» для студентов, обучающихся по специальности Автомобиле- и тракторостроение.– 2-е изд., переработанное и дополненное. М.: МАМИ, 2008. 76 с.: илл.
Учебное пособие ориентировано на изучение основ вычислительной математики и получение навыков в решении задач на ПЭВМ. В нём представлены наиболее распространенные методы вычисления определённых интегралов, решения нелинейных уравнений, систем линейных алгебраических уравнений, методы интерполяции и аппроксимации таблично заданных функций, а также методы решения задачи Коши для обыкновенных дифференциальных уравнений 1-го порядка. В качестве базового средства решения вычислительных задач используется Excel 2000.
© Московский государственный технический университет «МАМИ»
2008 г.
Введение
Создание новых и модернизация существующих технических, технологических, экономических и прочих объектов невозможно без детального исследования их поведения в реальных условиях. Существуют два подхода к такому исследованию. Первый из них заключается в создании реального образца объекта с последующим его экспериментальным изучением. Второй обычно применяют там, где нельзя провести весь комплекс исследований на самом объекте вследствие сложности его изготовления, выполнения требуемых измерений или значительных затрат на постановку необходимых экспериментов. Он состоит в применении специальных приёмов, называемых методами моделирования.
|
|
|
Методы моделирования основаны на понятии подобия различных объектов. При этом подобными называют объекты, параметры которых, определяющие их состояние, отличаются от исходных в заранее известное число раз, называемое масштабом подобия. Один из двух объектов, между которыми существует подобие, можно назвать объектом моделирования, а другой – его моделью. Подобие объектов может использоваться как при физическом, так и при математическом моделировании.
Физическое моделирование заключается в постановке экспериментов, как правило, с уменьшенной моделью объекта, несущей в себе все его исследуемые особенности. При этом круг исследований и их сложность не изменяются, как если бы все исследования проводились на самом объекте. Математическое моделирование основано на том, что реальные процессы, протекающие в объекте моделирования и характеризующие его свойства, могут быть описаны определёнными математическими соотношениями. Совокупность математических соотношений, позволяющих описать исследуемые свойства объекта, называют его математической моделью.
Построение математической модели начинают с формализованного описания объекта, в которое включают процессы, наиболее существенные для задачи моделирования. Каждый из выбранных процессов описывается в форме тех или иных уравнений, что позволяет при последующем объединении этих уравнений в систему относительно общих параметров получить математическую модель исследуемого объекта.
|
|
|
Такая математическая модель сама по себе ещё не дает возможности судить о поведении объекта моделирования. Исследование моде-
лирующей системы математических уравнений позволяет сделать лишь ряд качественных выводов о поведении объекта, исходя из их общего вида, да и то лишь в относительно простых случаях. Поэтому для изучения свойств объекта по его математическому описанию нужно решить систему уравнений, составляющую это описание, и получить результаты, аналогичные измерениям на физической модели. Другими словами, необходим алгоритм решения системы уравнений математической модели, который позволит осуществить собственно процесс моделирования.
Математическое описание реальных объектов представляет собой достаточно сложные системы уравнений. Поэтому математическое моделирование практически возможно только при использовании вычислительных машин.
Повсеместное использование программ обработки электронных таблиц во многом объясняется их широкими возможностями. Рассматриваемая в пособии программа Excel 2000 относится к программам данного класса и может быть использована для решения задач обработки заказов и планирования производства, расчёта налогов и заработной платы, учёта кадров, издержек, управления сбытом, имуществом и во многих других областях деятельности. Однако область применения программы не ограничивается только сферой деловой жизни. Благодаря мощным математическим и инженерным функциям с её помощью можно решать некоторые задачи в области естественных и технических наук.
Программа Excel 2000 входит в группу программ Microsoft Office и для обеспечения взаимодействия и совместимости с другими программами оснащена как модулем базы данных, реализующим доступ к внешним базам данных, так и модулем программирования, который позволяет автоматизировать решение вычислительных задач с использованием других прикладных программ фирмы Microsoft.
Предполагается, что студенты уже знакомы с основами работы с программой Excel. В методических указаниях рассмотрены возможности применения электронных таблиц для проведения расчётов, возникающих при решении технических и экономических задач и требующих знаний определённых разделов вычислительной математики.
|
|
|
ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Справочная информация
При решении инженерных задач возникают ситуации, когда аналитическое вычисление определённого интеграла затруднено или невозможно. В подобных ситуациях решение может быть получено одним из методов приближенного вычисления значения определённого интеграла.
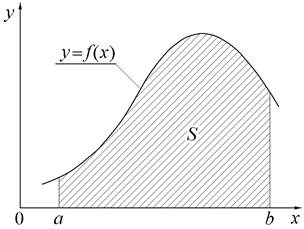 Все методы приближенного вычисления определённых интегралов основаны на геометрическом смысле интеграла Ньютона-Лейбница. Он заключается в том, что определенный интеграл
Все методы приближенного вычисления определённых интегралов основаны на геометрическом смысле интеграла Ньютона-Лейбница. Он заключается в том, что определенный интеграл

численно равен площади S криволинейной трапеции, ограниченной графиком подынтегральной функции f (x) и осью абсцисс на отрезке [ a, b ] (см. рис.1).
 Поэтому для приближённого вычисления определённого интеграла достаточно подсчитать площадь трапеции S. Можно указать множество способов вычисления площади S. Простейшие из них – формулы прямоугольников, трапеций и Симпсона.
Поэтому для приближённого вычисления определённого интеграла достаточно подсчитать площадь трапеции S. Можно указать множество способов вычисления площади S. Простейшие из них – формулы прямоугольников, трапеций и Симпсона.
Формула средних прямоугольников
 В формуле средних прямоугольников криволинейная трапеция представляется набором прямоугольников (см. рис.2). В этом случае площадь криволинейной трапеции представляется в виде суммы площадей этих прямоугольников, а интеграл I приближенно вычисляется по формуле
В формуле средних прямоугольников криволинейная трапеция представляется набором прямоугольников (см. рис.2). В этом случае площадь криволинейной трапеции представляется в виде суммы площадей этих прямоугольников, а интеграл I приближенно вычисляется по формуле
|

или в развёрнутом виде
 ,
,
где  – абсцисса центральной точки i -го участка разбиения отрезка [ a, b ], h = (b – a)/ n – шаг равномерного разбиения отрезка, n – количество участков разбиения.
– абсцисса центральной точки i -го участка разбиения отрезка [ a, b ], h = (b – a)/ n – шаг равномерного разбиения отрезка, n – количество участков разбиения.
Формула трапеций
 Аналогично вычисляется определённый интеграл по формуле трапеций, где площадь криволинейной трапеции S заменяется суммой площадей элементарных трапеций (см. рис.3). Такой подход приводит к вычислению определённого интеграла I по формуле
Аналогично вычисляется определённый интеграл по формуле трапеций, где площадь криволинейной трапеции S заменяется суммой площадей элементарных трапеций (см. рис.3). Такой подход приводит к вычислению определённого интеграла I по формуле


или, раскрывая сумму,
 .
.
Формула Симпсона ( J.Gregory (Грегори) 1668, Th.Simpson 1743 )
|
|
|
В формуле Симпсона площадь криволинейной трапеции рассчитывается как сумма площадей ряда криволинейных трапеций, у которых криволинейная сторона представляет собой участок параболы, проходящей через три соседние точки на графике подынтегральной функции. Это можно видеть на рис.4. Поэтому число участков разбиения отрезка [ a,b ] в отличие от предыдущих способов обязательно должно быть чётным. Исходя из этого, значение определённого интеграла приближённо вычисляется по формуле

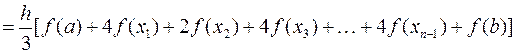 .
.
Реализация формул
Основой реализации любого вычислительного метода в программе Excel является представление его алгоритма в виде таблицы. При этом часто используется следующий подход: столбцами таблицы являются последовательно получаемые промежуточные результаты расчёта при одном значении аргумента или на одной итерации, а строками – последовательность значений аргумента или итерации. Иногда из этой закономерности выпадает первая строка таблицы, так как её используют для ввода начальных значений.
Описанный выше подход к формированию расчётной таблицы не является догмой. Каждый пользователь вправе использовать свой подход, но обычно он в той или иной мере основывается на описанных выше принципах.
Пример. Вычислить в программе Excel интеграл

с шагом интегрирования h = 0.1.
Для вычисления значения интеграла можно воспользоваться формулой средних прямоугольников. Одна из возможных её реализаций представлена таблицей 1 следующего вида (см. формулу)
Таблица 1.
| i | xi | 
| 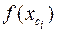
|
| x 0 | 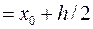
| 
| |
| x 1 | 
| 
| |
| … | …. | ……… | ……… |
| n –1 | xn– 1 | 
| 
|

|
Столбец «i» не несет никакой информационной нагрузки, кроме пояснения к используемым формулам, а потому при реализации в программе Excel может быть опущен. Таблица интегрирования будет выглядеть следующим образом (см. рис.5)

Рис.5.
Результат интегрирования располагается в ячейке С12, где он вычисляется с помощью встроенной функции СУММ:
= 0,1*СУММ(С2:С11).
Аналогичным образом может быть построена таблица вычисления заданного интеграла по формуле трапеций (см. ниже рис.6)

Рис.6.
Так как в формуле трапеций все значения функции (кроме двух крайних) удваиваются, то в таблицу удобно ввести столбец С. При таком подходе интеграл в ячейке D13 тоже удобно вычислять с помощью функции СУММ.
Выбор ячейки D13 для записи результата может быть произвольным и делается только из соображений эстетики.
Доработав приведённую выше таблицу легко вычислить интеграл по формуле Симпсона (см. рис.7). Здесь так же используются дополнительные столбцы для записи отдельных групп слагаемых.
|
|
|

Рис.7.
Результат интегрирования располагается в ячейке E13.
Оценка погрешностей численных способов интегрирования
Точность вычисления любой величины определяется погрешностью, которая может быть представлена в абсолютной или относительной форме. Абсолютная погрешность величины есть модуль разницы между её точным и приближённым значениями. Например, между точным значением определённого интеграла и его значением, полученным выбранным численным способом при конкретном количестве участков разбиения отрезка [ a, b ]
 .
.
Относительная погрешность является более информативным параметром точности вычисления искомой величины. Она оценивает ошибку решения в долях точного (или лучшего из имеющихся) значения этой величины и вычисляется как модуль отношения разницы между точным и вычисленным значениями величины к её точному значению
 .
.
Анализ формул численного интегрирования непрерывно дифференцируемых на отрезке [ a, b ] подынтегральных функций f (x) позволяет получить следующие оценки абсолютных погрешностей вычисления интегралов:
- для формулы средних прямоугольников  ;
;
- для формулы трапеций  ;
;
- для формулы Симпсона  .
.
На практике, такое вычисление погрешностей при интегрировании затруднено, так как требует решения дополнительной, зачастую даже более сложной, задачи поиска максимума высших производных подынтегральной функции. Поэтому чаще для вычисления погрешности методов используют апостериорные оценки, базирующиеся на правиле Рунге (правило двойного счёта). В основу этого подхода к оценке погрешности методов интегрирования положено утверждение, заключающееся в том, что все формулы для погрешностей имеют одну и ту же структуру
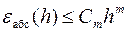 ,
,
где коэффициент Cm включает в себя длину участка интегрирования, максимум модуля производной и соответствующий коэффициент, а степень m определяется видом используемой формулы численного интегрирования (m = 2 для формул средних прямоугольников и трапеций и m = 4 для формулы Симпсона). Использование этой зависимости при уменьшении шага интегрирования вдвое позволяет записать погрешность вычисления интеграла в виде
 .
.
Сравнение последних двух формул даёт основное соотношение правила Рунге, справедливое для всех способов приближённого вычисления интеграла
 ,
,
где S (h /2) и S (h) – приближённые значения интеграла, вычисленные при шагах разбиения отрезка [ a, b ], отличающихся друг от друга в два
раза. Исходя из этого, для оценки погрешности вычисленного значения интеграла с выбранным шагом надо повторить вычисления, удвоив величину шага, и воспользоваться приведённым выше соотношением.
Например, если требуется вычислить рассмотренный выше интеграл с относительной погрешностью, не превышающей 0.5%, то для выполнения задания можно воспользоваться формулой средних прямоугольников, выбрав в качестве первоначального значения шага интегрирования h = 0.5, т.е. разбив отрезок [0, 1] на два участка с граничными точками 0, 0.5 и 1.0. Тогда приближённое значение интеграла будет S (0.5) = 0.5935. При уменьшении шага интегрирования вдвое (h = 0.25), т.е. при разбиении отрезка интегрирования на 4 участка, значение интеграла будет равно S (0.25) = 0.6095. Таким образом, абсолютная и относительная погрешности вычисления последнего значения интеграла могут быть вычислены по правилу Рунге
 ,
,
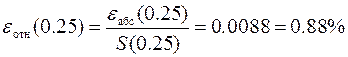 .
.
В связи с тем, что требуемая точность вычисления интеграла не достигнута, решение продолжается: шаг интегрирования уменьшается ещё в два раза (h = 0.125). В этом случае значение интеграла будет равно 0.6141, а его абсолютная и относительная погрешности составят 0.0046 и 0.75%, соответственно. Видно, что требуемая точность опять не достигнута, поэтому шаг интегрирования уменьшается ещё в два раза (h = 0.0625) и вычисления повторяются. С таким шагом значение интеграла получается равным 0.6152, его абсолютная погрешность – 0.0011, а относительная – 0.18%. Таким образом, при шаге интегрирования h = 0.0625 решение задачи, равное 0.6152, получено с заданной погрешностью.
Если постановка задачи требует получение результатов с меньшей погрешностью, чем была получена, то необходимо дальнейшее уменьшение величины шага разбиения отрезка интегрирования [ a, b ]. Однако этот процесс нельзя продолжать бесконечно. Он ограничивается точностью представления данных в ЭВМ: существует некоторое минимальное значение шага разбиения отрезка [ a, b ], дальнейшее уменьшение которого вызовет рост погрешности вычисления интеграла.
Контрольные задания
По номеру своего варианта вычислить один из приведённых ниже определённых интегралов с относительной погрешностью не превышающей 0.001. Для вычисления интеграла использовать указанный преподавателем метод из числа рассматриваемых в этой лабораторной работе.
1. 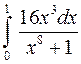 . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  .
.
5. 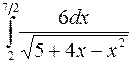 . 6.
. 6.  . 7.
. 7.  .
.
8.  . 9.
. 9.  . 10.
. 10. 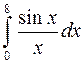 . 11.
. 11. 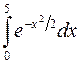 .
.
12.  . 13.
. 13.  . 14.
. 14.  .
.
15.  . 16.
. 16.  . 17.
. 17.  . 18.
. 18.  .
.
19.  . 20.
. 20. 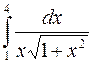 . 21.
. 21.  .
.
22.  . 23.
. 23.  . 24.
. 24.  . 25.
. 25.  .
.
26.  . 27.
. 27. 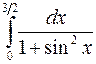 . 28.
. 28.  .
.
29.  . 30.
. 30. 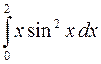 .
.
2. РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Справочная информация
 Как известно, далеко не всякое алгебраическое уравнение
Как известно, далеко не всякое алгебраическое уравнение  может быть решено аналитически. Это относится к большинству трансцендентных уравнений и к алгебраическим уравнениям выше четвёртого порядка. Однако точное решение уравнений на практике часто и не требуется. Чтобы считать задачу решённой, достаточно бывает отыскать значения корней с требуемой степенью точности. Для получения таких решений разработаны численные методы.
может быть решено аналитически. Это относится к большинству трансцендентных уравнений и к алгебраическим уравнениям выше четвёртого порядка. Однако точное решение уравнений на практике часто и не требуется. Чтобы считать задачу решённой, достаточно бывает отыскать значения корней с требуемой степенью точности. Для получения таких решений разработаны численные методы.
 Решение нелинейных уравнений осуществляется в два этапа. На первом этапе производится отделение корней, то есть поиск достаточно малых отрезков локализации, каждый из которых содержит единственный корень уравнения и на каждом из которых функция f (x) монотонна вместе со своей первой производной. Для этого используется график функции y = f (x), точки пересечения которого с осью абсцисс являются корнями исходного уравнения.
Решение нелинейных уравнений осуществляется в два этапа. На первом этапе производится отделение корней, то есть поиск достаточно малых отрезков локализации, каждый из которых содержит единственный корень уравнения и на каждом из которых функция f (x) монотонна вместе со своей первой производной. Для этого используется график функции y = f (x), точки пересечения которого с осью абсцисс являются корнями исходного уравнения.
Случай, когда корнем уравнения является точка касания графика и оси абсцисс, здесь не рассматривается. Это позволяет выделить отрезки [ a, b ], содержащие только один корень (см. рис.1). При этом для непрерывной функции f (x) будет выполняться неравенство f (a) f (b) < 0.
Процесс отделения корней может быть проиллюстрирован на примере уравнения x 3 – 7.3 x 2 + 16.8 x – 12.2 = 0, для которого корни ищутся на отрезке [0, 3]. Сначала выполняется процесс табулирования функции f (x)= x 3 – 7.3 x 2 + 16.8 x – 12.2, а затем, используя полученные результаты, строится диаграмма типа «гладкие графики» (см. рис.2). Как видно из графика функции, на этом этапе можно выделить два отрезка локализации корней [1.5, 1.6] и [2.2, 2.4].
На втором этапе внутри выделенных отрезков вычисляются значения каждого из корней уравнения с заданной точностью. Для этого используются два основных итерационных подхода: последователь-

Рис.2.
ное уточнение первоначального приближения значения корня, взятого из выделенного отрезка, и сужение выделенного отрезка, содержащего корень.
Методы последовательного уточнения начального приближенного значения корня. К этим методам относятся метод простых итераций, метод Ньютона и ряд других. Ониобладают высокойэффективностью, но их применение связано с рядом ограничений, накладываемых на свойства функции f (x).
Метод Ньютона ( I.Newton, 1669, Mr.Raphson, 1720 )
В данном методе каждое новое приближение к значению корня уравнения f (x) = 0 ищется по следующей итерационной схеме


………………….

………………….
где x 0 – первоначальное приближенное значение корня, взятое с отрезка [ a, b ] локализации точного решения уравнения.
Если последовательность значений xk (k = 0, 1, 2,...) сходится к точному значению корня x т, то абсолютная погрешность значения корня на k -ом шаге (xk) определяется выражением
 ,
,  ,
,
где
 ,
, 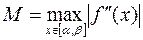 ,
, 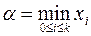 ,
,  .
.
Приведённые формулы для вычисления погрешностей требуют решения дополнительной задачи поиска минимума модуля первой производной функции f (x) и максимума модуля её второй производной на отрезке локализации корня [ a, b ]. В связи с этим на практике итерации завершают при выполнении одного из условий:
 или
или  ,
,
где δ абс и δ отн – задаваемые абсолютная и относительная разницы между соседними значениями приближения корня, соответственно. В этом случае надо помнить, что истинная погрешность определения корня может заметно отличаться от δ абс или δ отн. Поэтому после завершения поиска корня необходимо вычислить истинное значение погрешности решения по приведённым формулам для ε абс или ε отн.
Может случиться так, что последовательность приближённых значений xk (k = 0, 1, 2,...) корня x т не имеет предела. В этом случае метод расходится, и описанная итерационная схема не может быть применена для решения уравнения. Анализ выражения для ε абс позволяет сформулировать условие сходимости итераций. Очевидно, для того, чтобы погрешность ε абс при стремлении k к бесконечности стремилась к нулю и итерации сходились к точному решению, надо обеспечить выполнение следующего неравенства
 .
.
При решении практических задач точное значение x т корня уравнения неизвестно. Поэтому вместо приведённой формулы для абсолютной погрешности используют её аналоги
 ,
,  ,
,
где  ,
,  в первом случае и
в первом случае и 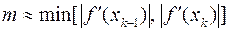 ,
, 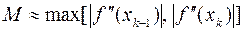 во втором.
во втором.
Для проверки итерационной схемы на сходимость применяется неравенство, подобное приведённому выше
 ,
,
где
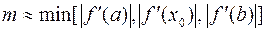 ,
,  .
.
При использовании этого неравенства надо помнить, что выбор значений границ отрезка локализации a и b существенно влияет на результаты проверки. Поэтому их надо выбирать так, чтобы они достаточно близки к x 0.
Графическая интерпретация работы метода Ньютона представлена на рис.3. Из точки на кривой y = f (x), имеющей абсциссу x 0, проводит  ся касательная до пересечения с осью 0 x. Абсцисса точки пересечения принимается за новое приближение значения x 1 корня уравнения f (x) = 0. В случае сходимости последовательности вычисляемых значений x 0, x 1,…, xk,… процесс продолжается до тех пор, пока не выполнится условие его окончания.
ся касательная до пересечения с осью 0 x. Абсцисса точки пересечения принимается за новое приближение значения x 1 корня уравнения f (x) = 0. В случае сходимости последовательности вычисляемых значений x 0, x 1,…, xk,… процесс продолжается до тех пор, пока не выполнится условие его окончания.
 Рассмотрим работу метода Ньютона на примере поиска приближённого значения корня уравнения
Рассмотрим работу метода Ньютона на примере поиска приближённого значения корня уравнения
x 3 – 7.3 x 2 + 16.8 x – 12.2 = 0
на отрезке [1, 2] и оценки погрешности его определения.
На первом этапе необходимо построить график левой части уравнения, для чего вычисляются её значения в трёх базовых точках
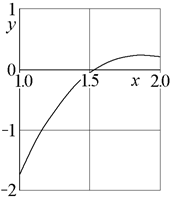 f (1.0) = 1.03 – 7.3·1.02 + 16.8·1.0 – 12.2 = – 1.70,
f (1.0) = 1.03 – 7.3·1.02 + 16.8·1.0 – 12.2 = – 1.70,
f (1.5) = 1.53 – 7.3·1.52 + 16.8·1.5 – 12.2 = – 0.05,
f (2.0) = 2.03 – 7.3·2.02 + 16.8·2.0 – 12.2 = 0.20.
Как видно на рис.4, в качестве начального приближения корня рассматриваемого уравнения можно взять x 0= 1.5.
 Теперь, следуя итерационной схеме метода Ньютона, можно вычислить первое приближение корня
Теперь, следуя итерационной схеме метода Ньютона, можно вычислить первое приближение корня
 ,
,
где
f (x 0) = f (1.5) = 1.53 – 7.3·1.52 + 16.8·1.5 – 12.2 = –0.05,
 = 3·1.52 – 14.6·1.5 + 16.8 = 1.65,
= 3·1.52 – 14.6·1.5 + 16.8 = 1.65,
Отсюда получается значение корня в первом приближении
 .
.
Вторая итерация:
f (x 1) = 1.53033 – 7.3·1.53032 + 16.8·1.5303 – 12.2 = –0.00254,
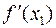 = 3·1.53032 – 14.6·1.5303 + 16.8 = 1.48306,
= 3·1.53032 – 14.6·1.5303 + 16.8 = 1.48306,
 .
.
Третья итерация:
f (x 2) = 1.5320183 – 7.3·1.5320182 + 16.8·1.532018 – 12.2 = –8·10 –6,
 = 3·1.5320182 – 14.6·1.532018 + 16.8 = 1.47378,
= 3·1.5320182 – 14.6·1.532018 + 16.8 = 1.47378,
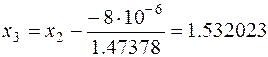 .
.
Относительная разница между значениями приближения корня на второй и третьей итерациях составляет
 .
.
Таким образом, если в задаче требовалось бы вычислить значение корня с относительной погрешностью εотн= 0.00001, то уточнение значения корня можно прекратить. Однако истинное значение абсолютной и относительной погрешностей требуется уточнить по формулам
 ,
, 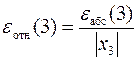 ,
,
где
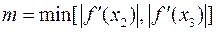 ,
, 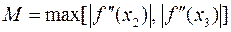 .
.
Часть результатов известна, а остальные необходимо досчитать:
 ,
,
 = 3·1.5320232 – 14.6·1.532023 + 16.8 = 1.47375,
= 3·1.5320232 – 14.6·1.532023 + 16.8 = 1.47375,
 .
.
Вторая производная функции имеет вид
 ,
,
откуда
 = 6·1.532018 – 14.6 = –5.40789,
= 6·1.532018 – 14.6 = –5.40789,
 = 6·1.532023 – 14.6 = –5.40786,
= 6·1.532023 – 14.6 = –5.40786,
 .
.
Тогда абсолютная погрешность вычислений будет составлять
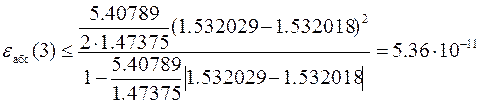 ,
,
а относительная примет значение
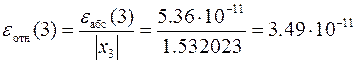 .
.
Выполненные вычисления без определения истинного значения относительной погрешности могут быть сведены в таблицу 1:
Таблица 1.
| i | xi | 
| 
|
| x 0 | 
| 
| |
| x 1 | 
| 
| |
| … | ….. | ………… | ….. |
При реализации в программе Excel эта расчётная таблица метода Ньютона может быть представлена аналогичным образом. Ниже на рис.5 она приведена вместе с результатами расчетов.
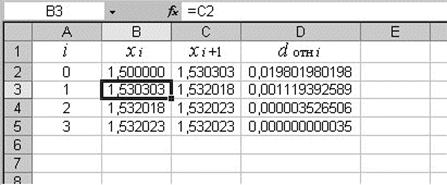
Рис.5.
Методы сужения отрезка [ a, b ], к которым относятся метод хорд, метод половинного деленияи др., не имеют ограничений на функцию f (x), присущих методам последовательного уточнения.
Метод половинного деления (метод бисекций)
Алгоритм метода иллюстрируется на рис.6. Отрезок локализации [ a, b ] корня делится пополам x 1= (a + b)/2 и в полученной точке вычисляется значение функции. Если f (x 1) = 0, то корень найден и расчёты прекращают. В противном случае выбирается новый отрезок, содержащий корень уравнения, из отрезков [ a, x 1] и [ x 1, b ]. На концах искомого отрезка функция f (x) должна иметь значения разного знака. Для этого проверяется условие f (a) f (x 1) < 0. При его выполнении в качестве нового отрезка принимается отрезок [ a, x 1], в противном случае – [ x 1, b ]. Процесс вычисления значения корня продолжается до тех пор, пока не будет выполнено требование к точности его определения. В данном случае оценка абсолютной погрешности определения корня


совпадает с длиной отрезка его последней локализации. В свою очередь относительная погрешность вычисляется как

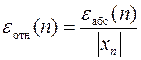 .
.
При этом за значение корня принимается либо одна из границ суженного отрезка [ a, b ], либо его середина.
Алгоритм метода может быть проиллюстрирован на рассмотренном выше примере уточнения корня уравнения
x 3 – 7.3 x 2 + 16.8 x – 12.2 = 0.
В качестве отрезка локализации выбирается отрезок [1.5, 1.6], содержащий первый корень уравнения (см. пример в описании метода Ньютона). На первом шаге уточнения корня вычисляются значения функции на границах выбранного отрезка
f (1.5) = 1.53 – 7.3·1.52+ 16.8·1.5 – 12.2 = – 0.05,
f (1.6) = 1.63 – 7.3·1.62+ 16.8·1.6 – 12.2 = 0.088.
Затем в середине интервала x 1 = 1.55 также вычисляется значение функции
f (1.55) = 1.553 – 7.3·1.552+ 16.8·1.55 – 12.2 = 0.0256.
Так как эта точка не соответствует корню уравнения, то определяется новый отрезок его локализации. Для этого проверяется знак произведения значений функции на левой границы отрезка локализации корня и в его центре f (1.5)· f (x 1). Из расчётов видно, что это произведение меньше нуля, значит, в качестве нового отрезка локализации корня должен приниматься отрезок [1.5, 1.55].
Для выполнения второго шага уточнения корня значения функции на границах нового отрезка локализации считать не нужно, они уже известны: f (1.5) = – 0.05; f (1.55) = 0.0256. Достаточно вычислить её значение в середине нового отрезка локализации корня x 2= 1.525
f (1.525) = 1.5253– 7.3·1.5252+ 16.8·1.525 – 12.2 = – 0.0105.
Так как произведение f (1.5) f (x 2) больше нуля, то в качестве нового отрезка локализации принимается [1.525, 1.55]. Аналогично выполняются шаги c третьего по седьмой, дающие следующие значения приближения корня
x 3= 1.5375 – центр отрезка [1.525, 1.55],
x 4= 1.53125 – центр отрезка [1.525, 1.5375],
x 5= 1.53438 – центр отрезка [1.53125, 1.5375],
x 6= 1.53281 – центр отрезка [1.53125, 1.53438],
x 7= 1.53203 – центр отрезка [1.53125, 1.53281].
Значение относительной погрешности вычисления приближения x 7= 1.53203 корня уравнения будет определяться по формуле
 .
.
Эта величина совпадает с длиной отрезка локализации найденного приближения корня, отнесённой к величине этого приближения
 .
.
Таким образом, если в задаче требовалось бы вычислить значение корня с относительной погрешностью ε отн = 0.002, то уточнение значения корня можно прекратить.
При реализации метода расчётная таблица может быть составлена в следующем виде:
Таблица 2.
| i | ai | bi | f (ai) | 
| f (xi) | 
|
| a 1 | b 1 | f (a 1) | x 1 | f (x 1) | 
| |
| Если f (a 1) f (x 1)<0, то a 2 = a 1, иначе a 2 = x 1. | Если f (a 1) f (x 1) 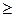 0, то b 2 = b 1, иначе b 2 = x 1. 0, то b 2 = b 1, иначе b 2 = x 1.
| f (a 2) | x 2 | f (x 2) | 
| |
| … | ….……… | …….…… | …… | ….. | …… | ……. |
Ниже на рис.7 представлены результаты расчётов в программе Excel.

Рис.7.
Контрольные задания
Найти все лежащие на указанном отрезке корни уравнения с относительной разницей между соседними значениями приближения каждого корня не более чем 0.00001. Для этого реализовать указанный преподавателем метод. Оценить относительную погрешность полученных значений корней.
1.  , (0 £ x £ 4). 2.
, (0 £ x £ 4). 2.  , (2 £ x £ 10).
, (2 £ x £ 10).
3.  , (0 £ x £ 4). 4.
, (0 £ x £ 4). 4. 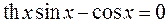 , (0 £ x £ 8).
, (0 £ x £ 8).
5. 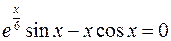 , (3 £ x £ 12). 6.
, (3 £ x £ 12). 6.  , (0 £ x £ 4).
, (0 £ x £ 4).
7.  , (0 £ x £ 4). 8.
, (0 £ x £ 4). 8.  , (0 £ x
, (0 £ x


