Кусочно-линейная интерполяция

Кусочно-линейная интерполяция состоит в представлении таблично заданной функции на каждом отрезке между абсциссами узловых точек линейной зависимостью y = a ₁+ a ₂ x так, как это показано на рис.2. Коэффициенты a ₁ и a ₂ определяются для каждого отрезка [ x_{i –1}, x_i ] в отдельности из условий

.

В результате кусочно-линейная приближающая функция на отрезке [ x_{i –1}, x_i ] имеет вид

,

и является непрерывной, однако её первая производная оказывается кусочно-непрерывной функцией, которая в каждом узле интерполяции имеет точку разрыва первого рода. Это часто накладывает существенные ограничения на её дальнейшее использование.

x
y		0.5

Рассмотрим работу метода на примере кусочно-линейной интерполяции таблично заданной функ­ции и поиска её значения при аргументе х = 1.6.

Для решения этой задачи строятся линейные функции для каждого отрезка между узловыми точками таблицы:

для отрезка [0, 1] между первой и второй точками

,

для отрезка [1, 2] между второй и третьей точками

,

для отрезка [2, 3] между третьей и четвёртой точками

,

Таким образом, табличная функция в случае кусочно-линейной интерполяции представляется в виде функции

Значение интерполирующей функции в заданной точке x = 1.6, принадле­жа­щей отрезку [1, 2] будет

y (1.6) = 0.5 + 0.5(1.6 – 1) = 0.8.

Ниже на рис.3 представлен фрагмент рабочей книги Excel с реализацией метода кусочно-линейной интерполяции. При построении графика приближающей функции аргумент х изменяется с шагом 0.2, а значения функции вычисляются по общей формуле, адаптированной под конкретные значения диапазонов аргумента.

Рис.3.

Как видно из рисунка для аргумента x = 1.6 расчёты, проведенные программой Excel, дали значение 0.8.

 

Многочлен Лагранжа (J.L.Lagrange, 1795)

Представляет собой случай полиномиального представления приближающей функции, когда она ищется в виде линейной комбинации базисных функций j_k (x), которые должны быть определены для всего отрезка интерполяции [ x ₁, x_n ], линейно независимы, и их количество должно быть равно числу узлов таблично заданной функции

.

Коэффициенты a ₁, a ₂,..., a_n определяются исходя из условий равенства значений приближающей и исходной функций при табличных значениях аргумента, что сводит задачу к системе n линейных алгебраических уравнений относительно них, а в качестве функций j_k (x) используются полиномы (n –1) степени

,

которые для пяти узловых точек записываются в виде

,

,

,

,

.

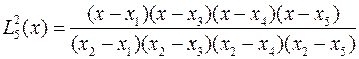Для каждого полинома характерно то, что для всех значений x_i в узловых точках он принимает нулевые значения, кроме k -ой, где его значение равно единице.

Графики этих полиномов пред­ставлены на рис.4.     При таком выборе базисных функций коэффициенты приближающей функции оказываются ординатами таблично заданной функции, а сама она приобретает харак-

терный для многочлена Лагранжа вид:

.

Процесс построения интерполирующего многочлена Лагранжа для пяти узловых точек показан на рис.5.

Рассмотрим работу метода на приведенном выше примере. Сначала строятся четыре базовых полинома:

,

,

,

.

Они позволяют записать интерполирующий многочлен Лагранжа в виде

Для аргумента x = 1.6 многочлен Лагранжа даёт

Ниже на рис.6 представлен фрагмент рабочей книги Excel с реализацией интерполяции с помощью многочлена Лагранжа.

Рис.6.

Как видно из рисунка для аргумента x = 1.6 многочлен Лагранжа дал значение 0.528.

Для контроля правильности вычислений многочлена Лагранжа полезно строить графики базовых полиномов. Для рассматриваемого примера они приведены на рис.7.

Рис.7.

 

Контрольные задания

С помощью одного из методов интерполяции сформировать образ кривой, визуально совпадающий с графиком заданной функции. В качестве такой функции взять левую часть алгебраического уравнения из лабораторной работы №2, которая соответствует номеру выполняемого варианта. В качестве отрезка интерполяции использовать указанный там же отрезок поиска корней. Точки интерполяции (в количестве 5–7 штук) распределить на заданном отрезке по своему усмотрению наилучшим образом.

 

5. АППРОКСИМАЦИЯ ТАБЛИЧНО ЗАДАННЫХ ФУНКЦИЙ

Справочная информация

Интерполяция на практике используется только в тех случаях, когда значения координат узлов таблично заданной функции не искажены случайными ошибками. Наличие ошибок в значениях таблично заданной функции приводит к неправильному представлению о поведении реальной функции и, как следствие этого, делает бес­смыс­ленной её интерполяцию. В этом случае рекомендуется строить «сглаживающую» приближающую функцию, отражающую физику моделируемого процесса. Её график не обязан проходить через все узловые точки табличной функции, как показано на рис.1. Построение таких приближающих функций носит название аппро­ксимации.

Через множество узловых точек таблично заданной функции можно провести бесконечное количество аппроксимирующих кривых. Задача выбора единственной из них определяется двумя основными моментами:

- выбор аналитических зависимостей, отражающих физику взаимосвязи аргумента и реальной функции, когда должен быть определен общий вид приближающей функции;

- выбор критерия достоверности описания реальной функции с помощью выбранных зависимостей.

Существует множество подходов к построению вида приближающей функции, как функции с параметрами. Одним из них является выбор в качестве аппроксимирующей зависимости линейной комбинации некоторых известных аналитических функций. Вместе они должны отражать суть физического процесса, описываемого исходной функцией, и быть линейно независимыми на отрезке аппроксимации [ x ₁, x_n ]

.

Функции φ_k (x) часто выбираются в виде полиномов, частным случаем которых являются степенные функции

φ ₁(x) = 1, φ ₂(x) = x, φ ₃(x) = x ², φ ₄(x) = x ³,…,

в виде тригонометрических косинусов

,

или в любом другом удобном для исследователя виде.

Другим подходом к построению приближающей функции является её представление сплайнами. Это избавляет исследователя от необходимости подбирать аналитические функции для аппроксимирующей зависимости и часто даёт результат, отвечающий всем требованиям, которые предъявляются к процессу аппроксимации.

В качестве критерия достоверности описания реальной функции Гауссом (1794) и Лежандром (A.M.Legendre, 1805) было предложено использовать сумму квадратов отклонений значений аппроксимирующей функции от ординат узлов таблично заданной

,

где отклонение от каждой узловой точки Δ _i, показанное на рис.2, вычисляется как

.

Сумма квадратов отклонений F при таком представлении является квадратичной функцией от параметров аппроксимации c ₁, c ₂,..., c_m. Очевидно, что чем меньше значение функции F, тем лучше выбранная аппроксимирующая функция описывает реальную функцию. Следовательно, задача аппроксимации сводится к определению значений параметров c ₁, c ₂, ..., c_m, которые минимизируют значение критерия – функции F. Этот приём получил название «метод наименьших квадратов».

Необходимым условием экстремума квадратичной функции многих переменных F является равенство нулю всех её частных производных по параметрам c ₁, c ₂,..., c_m

.

Можно показать, что для функции F, являющейся суммой квадратов отклонений, достаточные условия существования её минимума в стационарной точке выполняются тождественно. Поэтому условиями существования экстремума функции F можно пользоваться как условиями её минимума, что позволяет привести задачу аппроксимации n значений табличной функции к задаче решения системы из m линейных алгебраических уравнений с симметричной матрицей относительно этих параметров

,

где

,

.

Работа метода может быть проиллюстрирована на примере аппроксимации функции, заданной 8-ю узловыми точками, показанными на рис.3, и поиска её значения при х = 1.5.

Для построения зависимости, аппроксимирующей таблично или графически заданную функцию, исследователь должен подобрать аналитические функций, которые своей комбинацией отражают описываемый процесс. В данном случае исходная функция может быть описана как комбинация двух функций. Первая из них должна отражать обратно пропорциональную зависимость функции от аргумента в диапазоне от 0 до 2, а вторая – прямо пропорциональную зависимость в диапазоне от 2 до 4. Таким образом, в качестве аппроксимационной зависимости может быть принята следующая

.

Необходимо заметить, что данное представление аппроксимирующей зависимости не является единственным. Можно подобрать и другие комбинации элементарных функций, которые отражают общий характер рассматриваемой табличной функции.

В соответствии с приведённым выше алгоритмом сумма F квадратов отклонений аппроксимирующей функции от узловых точек записывается в виде

Вычисления по этой формуле удобнее выполнять, сняв с графика координаты узловых точек и сформировав из них следующую таблицу

i
x	0.5	0.5		1.5	1.5	2.5	3.5
y	0.9	0.8	0.5	0.5	0.4	0.4	0.5	0.5

В этом случае сумма квадратов отклонений будет

а её частные производные по параметрам c ₁ и c ₂, соответственно

Исходя из условия равенства нулю полученных частных производных, решение задачи сводится к решению системы из двух линейных алгебраических уравнений

.

Эта система имеет следующее решение c ₁= 0.1047, c ₂= 0.4013. Таким образом, аппроксимирующая функция имеет вид

.

Её значения при табличных значения аргумента приведены ниже

x	0.5		1.5	2.5	3.5
y	0.8550	0.5060	0.4246	0.4223	0.4811	0.5191

С их помощью может быть вычислено значение целевой функции F

которое определяет погрешность аппроксимации

, ,

где норма таблично заданной функции была вычислена следующим образом

.

Решение этой задачи на ПЭВМ в программе Excel будет несколько отличаться от приведенного выше «ручного счета». Программа Excel не позволяет производить аналитические преобразования, поэтому при вычислении коэффициентов системы линейных алгебраических уравнений следует использовать приведенные выше общие выражения. В данном случае они вычисляются с использованием следующих выражений:

, ,

,

, .

Решение задачи начинается с ввода исходных данных в виде таблицы значений сглаживаемой функции и её графика (см. рис.4). Затем выполняется вычисление коэффициентов системы уравнений, определяющей коэффициенты c ₁ и c ₂ аппроксимационной зависимости. Это делается в таблице, каждая строчка которой соответствует одной узловой точке. В последней строке столбцы суммируются для получения окончательных значений коэффициентов.

Система линейных алгебраических уравнений решается с использованием встроенной функции Excel’а построения обратной матрицы системы.

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: