 |
Дармовые методические рекомендации
|
|
|
|
Ознакомьтесь с приложением Roots, т.е. тщательно изучите его код. Обратите свое высочайшее внимание на использование строки статуса для вывода информации, обработчиков событий и вызова одних обработчиков событий из других. Также изучите, каким-таким феерическим способом строится график любой заданной функции, как он перестраивается при изменении размеров окна приложения.
В абсолютном соответствии со своим индивидуальным заданием разработайте алгоритм нахождения (всех) корней уравнения с заданной точностью. На всякий случай поясню, что корнем уравнения Y=A*X+B будет такое значение X, при котором Y==0, т.е. X== –B/A. Для случая данной линейной функции корень находится вульгарно просто и погрешность его определения совпадает с точностью того вещественного типа данных, который мы используем для вычислений.
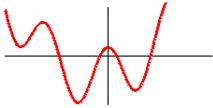
Поиск же корней некоторой произвольной функции Y=F(X) может оказаться не простым делом, если аналитическое выражение для корней функции получить нельзя. Например, на рис. 1 показан график некоторой функции, имеющей три корня в области ее определения, т.е. для Xmin<=X<=Xmax. Возможно, что у этой функции есть еще и другие корни, но мы ищем только те, которые попадают в заданную область определения.
|
Рис. 1. Прелестный график некоторой функции
Ясное дело, что можно находить корни графически: нарисовать на бумаге в клеточку, в известном масштабе график функции и получить корни на блюдечке с голубой каемочкой. Кстати, программа Roots отслеживает и выводит в строку статуса координаты мыши, в пикселях, и остается только пересчитать их в значения в те единицы, в которых заданы значения Х. Таким образом, мы уже имеем графический способ нахождения корней уравнения, не правда ли?
|
|
|
Теперь разберемся с погрешностью eps нахождения некоторого корня х1. Вычислим значение функции y1=F(x1) и будем считать, что мы определили корень х1 с заданной погрешностью eps, если выполняется условие |y1/Ymax|<=eps. И коню должно быть понятно, что Ymax – это максимальное значение функции в рассматриваемой области ее определения Xmin<=X<=Xmax.
Помимо графического метода нахождения корней существуют и другие.
1. Метод полного перебора, называемый часто методом «грубой силы. Разобьем весь диапазон определения функции на N точек, вычислим значение функции в каждой из них и, если значение каждого корня yк удовлетворяет условию |yк/Ymax|<=eps, будем считать задачу решенной. При этом требуется также найти такое минимальное N, при котором все корни отыскиваются с заданной погрешностью.
2. Стохастический метод. Будем генерировать случайные числа из диапазона определения функции, вычислять значение функции в этих точках, и, как и в методе полного перебора, находить корни, удовлетворяющие условию |yк/Ymax|<=eps. Подсчитать и вывести количество случайных значений, которое понадобилось для нахождения корней.
3. Метод дихотомии. Простейшим методом нахождения корней уравнения 
является метод деления пополам или дихотомия. Этот метод является интуитивно ясным и каждый действовал бы при решении задачи подобным образом. Алгоритм состоит в следующем.
Предположим, мы нашли две точки 
и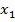 
, такие что 
и 
имеют разные знаки, тогда между этими точками находится хотя бы один корень функции 
.
Поделим отрезок 
пополам и введем среднюю точку 
.
Тогда либо 
, либо 
.
Оставим ту половину отрезка, для которой значения на концах имеют разные знаки. Теперь этот отрезок снова делим пополам и оставляем ту его часть, на границах которой функция имеет разные знаки, и так далее, достижения требуемой точности. Очевидно, постепенно мы сузим область, где находится корень функции, а, следовательно, с определенной степенью точности определим его. Заметьте, описанный алгоритм применим для любой непрерывной функции.
|
|
|
К достоинствам метода деления пополам следует отнести его высокую надежность и простоту. Недостатком метода является тот факт, что прежде чем начать его применение, необходимо найти две точки, значения функции в которых имеют разные знаки. Очевидно, что метод неприменим для корней четной кратности и также не может быть обобщен на случай комплексных корней и на системы уравнений.
Порядок сходимости метода линейный, на каждом шаге точность возрастает вдвое, чем больше сделано итераций, тем точнее определен корень.
Задание
В таблице 1 описаны функции, корни которых требуется найти.
Таблица 1
Варианты функций
| № | Функция и область определения | Вид графика | |||
| xmin=-5, xmax=5 a=-1,b=2,c=8, d=-10 y=a*x*x*x + b*x*x + c*x + d |
| ||||
| xmin=-15, xmax=10 a=-0.1,c=5 y=a*x*x + Math::Sin(x+0.5)*x + c |
| ||||
| xmin=-3.5, xmax=2 a=7, b=3, c=2, d=-5, e=1.5 y=a*Math::Cos(b*x) + c*x*x + d + e*x |
| ||||
| xmin=-1.8, xmax=2.2 a=1, b=1, c=2, d=1 y=(x+a) * (x+b) * (x-c) + d |
| ||||
| xmin=-5, xmax=3 a=-0.01,b=50,c=10 y=a*x*x + b*Math::Pow(Math::Sin(x+0.5),4)*x + c |
| ||||
| xmin=-3, xmax=2.5 a=-0.01, b=50, c=-20 y=a*x*x + b*Math::Pow(Math::Sin(x+0.5),5)*x + c |
| ||||
| xmin=-1.3, xmax=1.5 a=-0.01,b=50,c=-20 y=a*x*x + b*Math::Pow(Math::Sin(x+0.5),5)*x + c |
|
Выберите свой вариант задания из табл. 2. Вне зависимости от варианта задания ваше приложение должно удовлетворять следующим требованиям:
Ø значения коэффициентов (a,b,c...), область определения функции, погрешность eps и другие необходимые исходные данные должны вводиться пользователем в отдельной форме. В эту же или другую форму должны выводиться и результаты расчетов: значения корней, число интервалов по оси Х, затраченное время на поиск корней и др. полученные ценнейшие околонаучные результаты. Способ создания дополнительной формы рассмотрен в предыдущей работе;
Ø при перемещении мыши в окне в строке статуса должны выводиться текущие значения X и Y аргумента и значения функции (истинные, а не только в пикселях);
Ø найденные корни должны быть обозначены на графике так, как на рис. 1;
|
|
|
Ø оформить свой программный код в виде класса;
Ø само собой разумеется, что приложение должно иметь дружественный интерфейс, по крайней мере меню, а не какие-то там щелчки ЛКМ по форме, как в Roots.
Измерить время, затраченное на вычисления, можно таким образом:
DateTime d1 = DateTime::Now;// Получаем текущие дату и время
// выполняем длительные вычисления
DateTime d2 = DateTime::Now;// Вновь запрашиваем текущие дату и время
UInt64 ticks=d2.Ticks-d1.Ticks;/* Находим затраченное на вычисления
время в "тиках"*/
double msc=ticks/10000.;/*Переводим "тики" в мск*/
Таблица 2
Варианты индивидуальных заданий
| № | Номер функции из табл.1 | Метод нахождения корней |
| Метод полного перебора | ||
| Стохастический метод | ||
| Метод полного перебора | ||
| Стохастический метод | ||
| Метод полного перебора | ||
| Стохастический метод | ||
| Метод дихотомии | ||
| Стохастический метод | ||
| Метод полного перебора | ||
| Стохастический метод | ||
| Метод полного перебора | ||
| Стохастический метод | ||
| Метод полного перебора | ||
| Метод дихотомии |
|
|
|
