 |
Алгоритм расчета пластинок из нелинейно-деформируемого материала
|
|
|
|
Решение задачи изгиба пластинки из нелинейно-деформируемого материала методом упругих решений А.А. Ильюшина
Для получения численных результатов при расчете пластинок из нелинейно-деформируемого материала весомую долю занимают итерационные методы расчета такие как МУР А.А. Ильюшина и МППУ И.А. Биргера.
Применение таких методов расчета задач как методы Ритца-Тимошенко и Бубнова-Галеркина в полных функциях сводят решение задачи, описываемой нелинейными дифференциальными уравнениями при заданных граничных условиях, к системе нелинейных алгебраических уравнений, где впоследствии для решения этой системы уравнений можно использовать один из итерационных методов. Кроме этого, ряд названных итерационных методов ориентирован на решение нелинейных дифференциальных уравнений без ограничений на метод алгебраизации задачи или на способ аппроксимации диаграммы деформирования материала.
С помощью итерационных методов решение нелинейных задач заменяется последовательным решением линейных задач, но в виду того, что производится линеаризация нелинейных уравнений в большинстве случаев решение задачи становится громоздким, но вполне универсальным. Ниже будет рассмотрен итерационный метод, который может применяться при расчете пластинок из нелинейно-деформируемого материала и таким методом является метод упругих решений А.А. Ильюшина. Данный метод был первым из итерационных методов решения физически нелинейных задач, который был предложен еще в первой половине XX века А.А. Ильюшиным. Для применения этого метода необходимо иметь разрешающее дифференциальное уравнение решаемой задачи и соответствующие граничные условия.
|
|
|
Алгоритм расчета пластинок из нелинейно-деформируемого материала
Рассмотрим алгоритм применения метода упругих решений на примере задачи изгиба пластинки из нелинейно-деформируемого материала. При использовании теории малых упругопластических деформаций А.А. Ильюшина для несжимаемого тела с величиной коэффициента Пуассона µ=0,5 и при использовании кинематической модели прямых нормалей Кирхгофа получаем дифференциальное уравнение равновесия элемента пластинки из нелинейно деформируемого материала следующего вида:
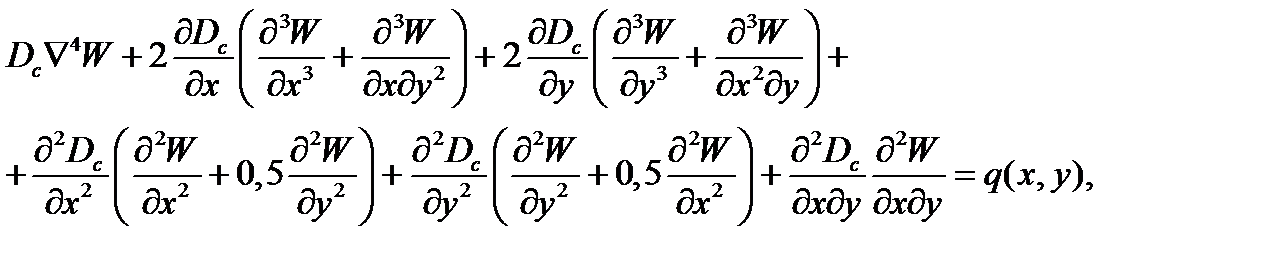
где переменная вдоль пространственных координат x, y жесткость пластинки при изгибе определяется из выражения

Здесь 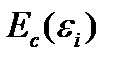 - секущий модуль, зависящий от величины интенсивности деформаций
- секущий модуль, зависящий от величины интенсивности деформаций 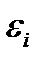 , являющейся, в свою очередь, функцией прогиба пластинки.
, являющейся, в свою очередь, функцией прогиба пластинки.
1. Для реализации алгоритма расчета пластинки в качестве примера, для аппроксимации экспериментальной диаграммы деформирования, примем кубическую параболу 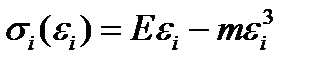 :
:
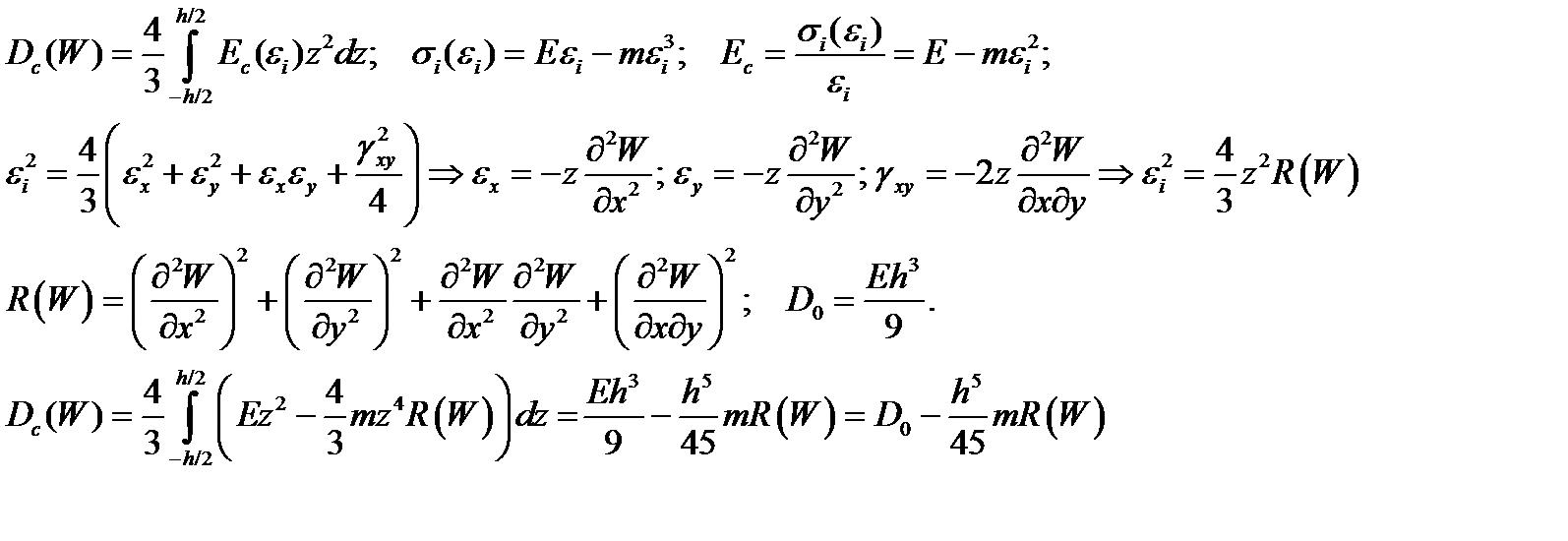
Где после соответствующих математических преобразований получаем окончательное выражение для переменной вдоль пространственных координат жесткости пластинки в следующем виде:

Где R(W) представляет собой квадратичную функцию прогиба пластинки, которая выражается следующим образом:

Далее приводим полученные выражения для переменной жесткости и квадратичной функции прогиба пластинки к безразмерному виду
Квадратичная функция прогиба пластинки в безразмерном виде выглядит следующим образом:
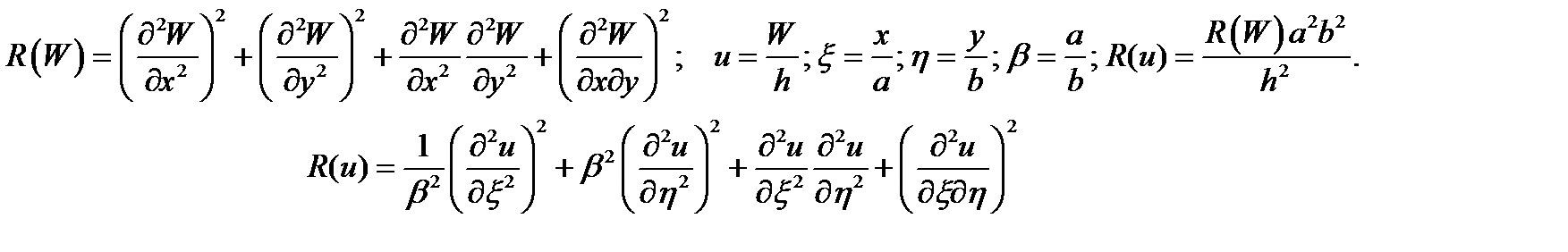
Переменная вдоль пространственных координат жесткость пластинки в безразмерном виде выражается следующим образом:

Переменная по длине пластинки жесткость в безразмерном виде:

При использовании коэффициентов заменяющих размерные координаты на безразмерные получим нелинейное дифференциальное уравнение изгиба пластинки из нелинейно-деформируемого материала в безразмерном виде:
|
|
|
 где
где 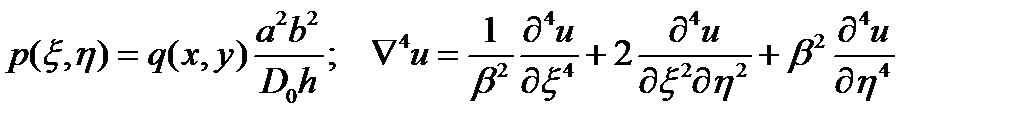 .
.
Как видно, из приведенного выше уравнения для изгиба пластинки из нелинейно-деформируемого материала, требуется получить производные от переменной жесткости пластинки.
Первая производная от переменной жесткости пластинки по безразмерным пространственным координатам:
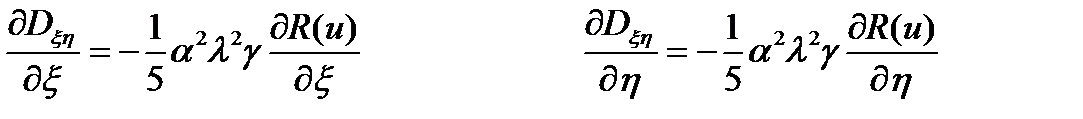
Вторая производная от переменной жесткости пластинки по безразмерным пространственным координатам:

Смешанная производная от переменной жесткости пластинки по безразмерным пространственным координатам:

Подставляем полученные выше выражения для производных от переменной жесткости в уравнение изгиба пластинки:
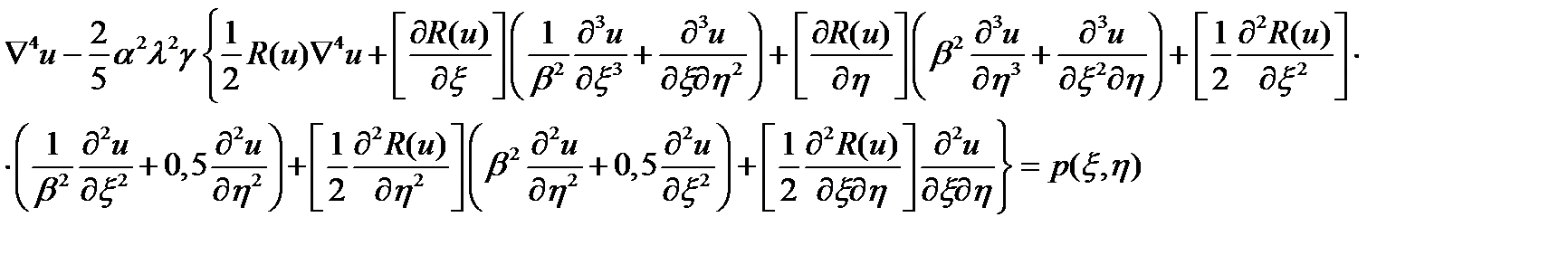
С учетом полученных выше замечаний отправим в представленном выше уравнении все нелинейные слагаемые в правую часть, а также расставим индексы номера приближения и в результате получим:
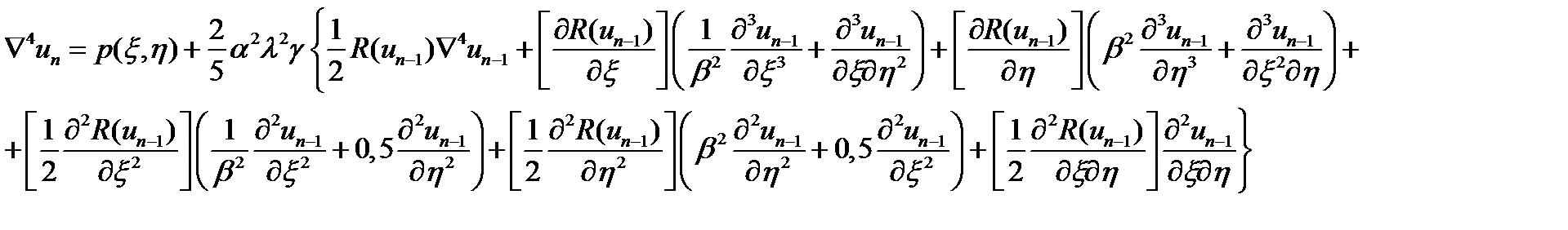
В первом приближении (n=1) решается обычная задача расчета пластинки из линейно-упругого материала:  . Это решение считаем начальным приближением решаемой задачи. Для получения решения нелинейной задачи строится следующий итерационный процесс.
. Это решение считаем начальным приближением решаемой задачи. Для получения решения нелинейной задачи строится следующий итерационный процесс.
При известном из первого приближения 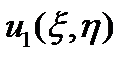 определяется скорректированная жесткость
определяется скорректированная жесткость  и соответствующие ей производные и затем решается уравнение вида:
и соответствующие ей производные и затем решается уравнение вида:

Решение которого позволяет определить уточненное решение для прогиба пластинки из нелинейно-деформируемого материала  .
.
Полагая далее n равным трем, четырем и так далее, получим все более точные приближения решаемой задачи. Итерационный процесс заканчивается при достижении требуемой точности вычислений, определяемой относительной разницей между результатами двух соседних приближений решения, а именно:

Уравнения метода А.А. Ильюшина, хоть и линейные, имеют переменные коэффициенты довольно общего вида, поэтому возникает проблема их численной реализации.
На каждой итерации МУР будем решать уравнения вариационным методом Бубнова-Галеркина в первом приближении. Прогиб представим в виде:
 ,
, 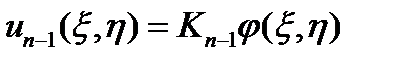
где  аппроксимирующая функция прогиба упругой пластинки, которая определяется статическим методом В.З. Власова.
аппроксимирующая функция прогиба упругой пластинки, которая определяется статическим методом В.З. Власова.
Уравнение метода Бубнова-Галеркина на произвольной итерации МУР в безразмерном виде выглядит следующим образом:
|
|
|

где функция описывающая нелинейную работу материала пластинки  выражается следующим образом:
выражается следующим образом:

а аппроксимирующая функция  .
.

При подстановке выражения для аппроксимирующей функции получим:

Поскольку интегралы перед искомой обобщенной координатой являются числами, то приводим полученное выше уравнение к более удобному виду:
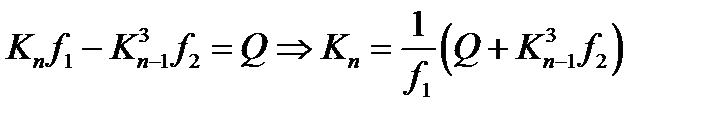
где коэффициенты перед неизвестными выглядят следующим образом:



Приведение коэффициента f2 к упрощенному виду:

Для пластинки с заданными условиями закрепления и нагрузкой построить аппроксимирующую функцию прогиба статическим методом В.З. Власова.
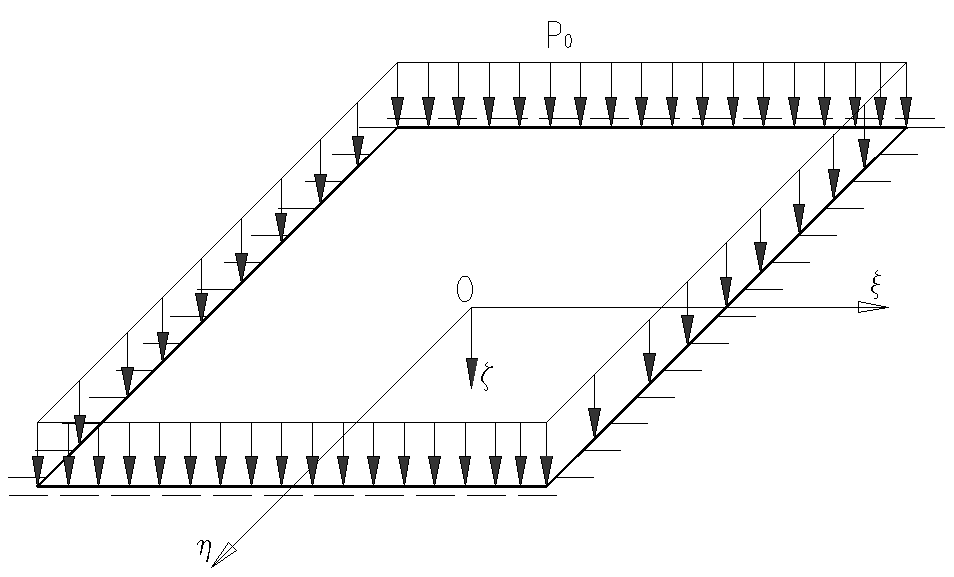
Рис. 2.
На основании статического метода В.З. Власова вырезаем из пластинки на рис. 2 две балки, соответственно, по направлениям ξ, η.
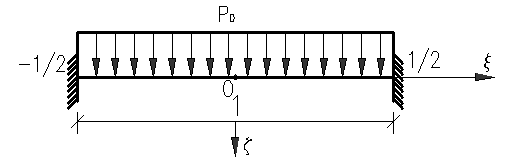
Рис. 3.

Используя граничные условия на концах балки 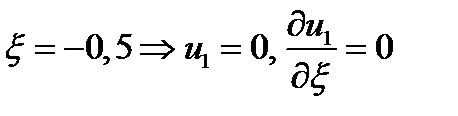 и
и  определяем произвольные постоянные интегрирования:
определяем произвольные постоянные интегрирования: 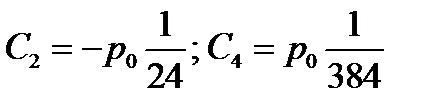 .
.
Записываем уравнение изгиба линейно-упругой балки, преобразуем его к виду  , коэффициент, стоящий перед скобкой полагаем равным 1 и получим аппроксимирующую функцию
, коэффициент, стоящий перед скобкой полагаем равным 1 и получим аппроксимирующую функцию


Рис. 4.

Используя граничные условия на концах балки  и
и  определяем произвольные постоянные интегрирования:
определяем произвольные постоянные интегрирования:  .
.
Записываем уравнение изгиба линейно-упругой балки, преобразуем его к виду 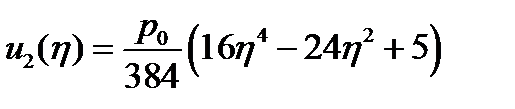 , коэффициент, стоящий перед скобкой полагаем равным 1 и получим аппроксимирующую функцию
, коэффициент, стоящий перед скобкой полагаем равным 1 и получим аппроксимирующую функцию

Функция аппроксимирующая прогиб пластинки из нелинейно-деформируемого материала:
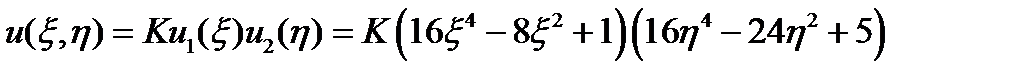
|
|
|


