Численная реализация полученных аналитических выражений

Исходные данные для пластинки:

Функция аппроксимирующая прогиб пластинки:

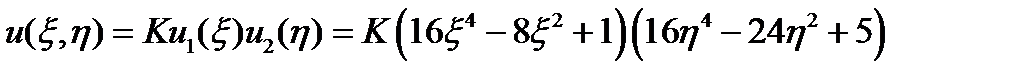
Определение обобщенной координаты K:

коэффициенты в данном уравнении выглядят следующим образом:

Приведение коэффициента f₂ к упрощенному виду:

 

 

Решение задачи изгиба пластинки из нелинейно-деформируемого материала методом переменных параметров упругости И.А. Биргера с использованием метода Бубнова-Галеркина

Метод переменных параметров упругости (МППУ) предложен И.А. Биргером для решения задач теории пластичности и ползучести. Для применения этого метода необходимо иметь дифференциальное уравнение решаемой задачи в полных функциях и соответствующие решаемой задаче граничные условия.

Дифференциальное уравнение изгиба пластинки из нелинейно-деформируемого материала при использовании теории малых упругопластических деформаций А.А. Ильюшина в размерном виде выглядит следующим образом:

где переменная вдоль пространственных координат x, y жесткость пластинки при изгибе определяется из выражения

Здесь 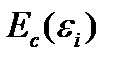- секущий модуль, зависящий от величины интенсивности деформаций 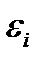, являющейся, в свою очередь, функцией прогиба пластинки.

Как и в предыдущих методах расчет начинается с построения функции, аппроксимирующей диаграмму деформирования материала балки, то есть с записи аналитического выражения .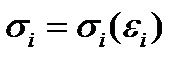

1. Примем кубическую параболу :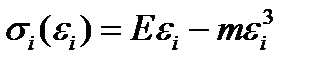

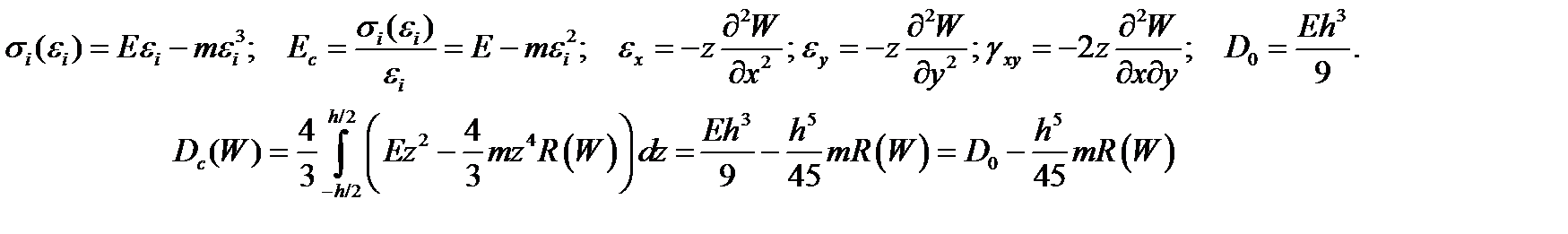После соответствующих математических преобразований получаем окончательное выражение для переменной вдоль пространственных координат жесткости пластинки в следующем виде:

 

Где R(W) представляет собой квадратичную функцию прогиба пластинки, которая выражается следующим образом:

Полученные ранее выражения для переменной жесткости, квадратичной функции и уравнение изгиба пластинки из нелинейно-деформируемого материала необходимо привести к безразмерному виду.

Квадратичная функция прогиба пластинки в безразмерном виде выглядит следующим образом:

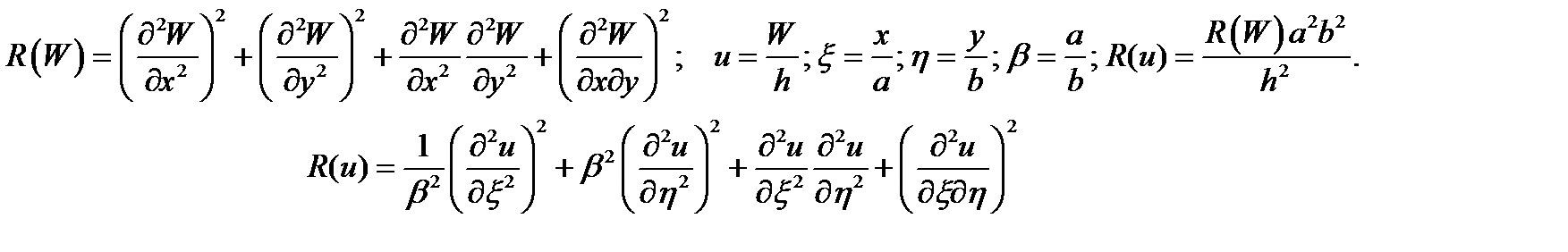
Переменная вдоль пространственных координат жесткость пластинки в безразмерном виде выражается следующим образом:

Переменная по длине пластинки жесткость в безразмерном виде:

При использовании коэффициентов заменяющих размерные координаты на безразмерные получим нелинейное дифференциальное уравнение изгиба пластинки из нелинейно-деформируемого материала в безразмерном виде:

где .

 

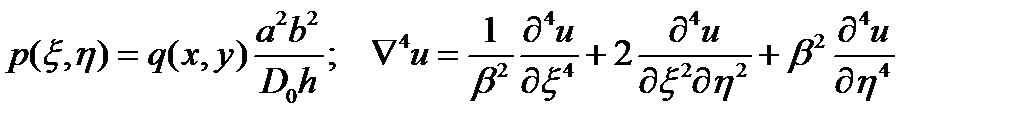Первая производная от переменной жесткости пластинки по безразмерным пространственным координатам:

 

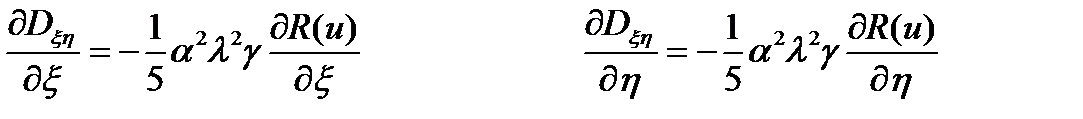
Вторая производная от переменной жесткости пластинки по безразмерным пространственным координатам:

Смешанная производная от переменной жесткости пластинки по безразмерным пространственным координатам:

Используя полученные выше выражения для производных от переменной жесткости запишем в требуемом виде уравнение метода переменных параметров упругости И.А. Биргера с расстановкой счетчиков итерационного процесса.

Расставив счетчики итерационного процесса в приведенном выше уравнении приведем выражения для переменной жесткости к удобному виду:

Сокращенная запись: .

Как видно из уравнения метода ППУ И.А. Биргера выражение для переменной вдоль пространственных координат жесткости пластинки в итерационном процессе будет отставать от искомого выражения для прогиба.

Выражения для переменной жесткости и ее производных:

Первая производная:

Вторая производная:

Смешанная производная:

Где квадратичная функция прогиба выглядит следующим образом:

При решении задачи в первом приближении (полагая n=1) решается задача расчета пластинки из линейно-упругого материала: 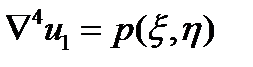. Решению этого уравнения соответствует точка пересечения касательной к нелинейной зависимости p-u в начале координат с горизонтальной прямой p_расч = const. Это решение считаем начальным приближением решаемой задачи. Для получения решения нелинейной задачи строится следующий итерационный процесс.

Имея величину прогиба u₁(ξ,η) можно определить скорректированную жесткость и, соответственно, ее производные .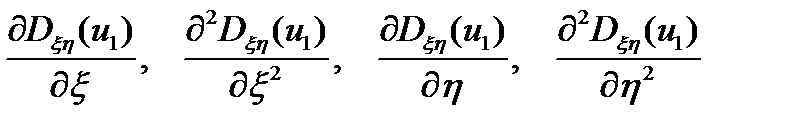

Затем решается уравнение вида:

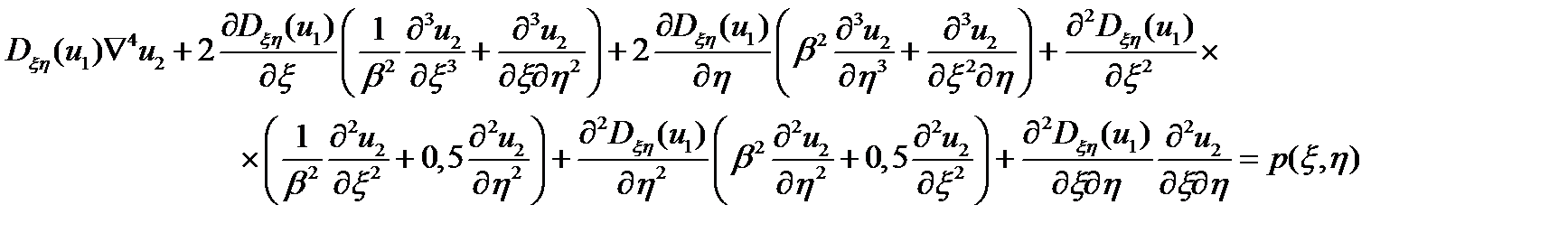
решение которого позволяет определить уточненное значение прогиба u₂(ξ,η).

Следовательно, на каждой итерации переменная жесткость нам известна, что позволяет проводить расчеты с произвольной диаграммой деформирования. Полагая далее n равным трем, четырем и так далее, получим все более точные приближения решаемой задачи.

Итерационный процесс заканчивается при достижении требуемой точности вычислений, определяемой относительной разницей между результатами двух соседних приближений решения, а именно:

Уравнения метода ППУ И.А. Биргера, хоть и линейные, имеют переменные коэффициенты довольно общего вида, поэтому возникает проблема их численной реализации. Поступим также, как мы поступили в методе упругих решений, а именно: будем решать на каждой итерации уравнение метода Бубнова-Галеркина в первом приближении.

В качестве выражения аппроксимирующего прогиб принимаем функцию полученную статическим методом В.З. Власова:

Уравнение метода Бубнова-Галеркина в сочетании с итерационным методом переменных параметров упругости И.А. Биргера:

Приведем полученное выше уравнение к удобному виду:

Определенные интегралы стоящие после искомых обобщенных координат обозначим как числовые коэффициенты:

 

 

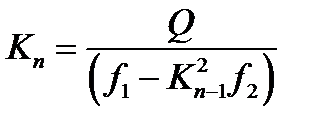
Где коэффициенты полученного выше уравнения выглядят следующим образом:

Квадратичная функция прогиба:

Бигармонический оператор Лапласа:

Приведение коэффициента f₂ к упрощенному виду:

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: