Решение задачи изгиба пластинки из нелинейно-деформируемого материала методом Бубнова-Галеркина в инкрементальной форме метода последовательных нагружений

Основное инкрементальное дифференциальное уравнение изгиба пластинки из нелинейно-деформируемого материала выглядит следующим образом:

В развернутом виде:

где переменная вдоль пространственных координат жесткость пластинки вычисляется по формуле:

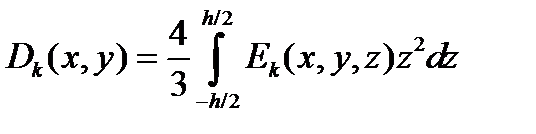
неизвестным в уравнении для изгиба пластинки из нелинейно-деформируемого материала является приращение прогиба Δ w.

Так как касательный модуль Е_k есть функция деформаций, которые, в свою очередь, выражаются через известный нам из предыдущих этапов нагружения накопленный прогиб пластинки W, то вычисление Е_k не представляет большого труда. Необходимо помнить, что жесткость пластинки изменяется вдоль её пространственных координат. Необходимые для решения уравнения граничные условия формулируются в приращениях прогиба.

Как и в предыдущих методах, расчет начинается с построения функции, аппроксимирующей диаграмму деформирования материала пластинки, то есть с записи аналитического выражения .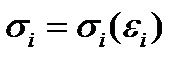

Аналитическая запись диаграммы деформирования необходима для вычисления интеграла вида:

И записи переменной жесткости в виде аналитической функции . Таким образом, для расчета пластинки необходимо решить обыкновенное линейное дифференциальное уравнение с переменными коэффициентами при заданных граничных условиях.

 

Расчет следует начинать с построения (выбора) аналитической функции, аппроксимирующей диаграмму деформирования материала балки (Построение (выбор) данной функции необходим для получения аналитического выражения касательного модуля). В данном случае аппроксимируем кривую деформирования кубической параболой , в результате чего выражение принимает следующий вид:

Минуя математические преобразования получаем окончательное выражение для переменной вдоль пространственных координат жесткости пластинки в следующем виде:

Где R(W) представляет собой квадратичную функцию прогиба пластинки, которая выражается следующим образом:

 

Далее приводим полученные выражения для переменной жесткости, квадратичной функции прогиба и уравнение изгиба пластинки из нелинейно-деформируемого материала к безразмерному виду:

Квадратичная функция прогиба пластинки в безразмерном виде выглядит следующим образом:

 

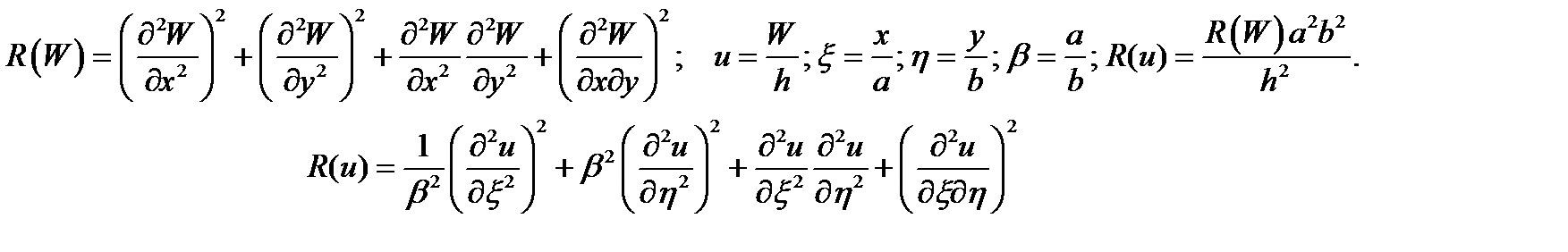
Выражение для переменной вдоль пространственных координат жесткости пластинки в безразмерном виде выглядит в следующим образом:

Переменная по длине пластинки жесткость в безразмерном виде:

При использовании коэффициентов заменяющих размерные координаты на безразмерные получим нелинейное дифференциальное уравнение изгиба пластинки из нелинейно-деформируемого материала в безразмерном виде в инкрементальной форме метода последовательных нагружений:

где .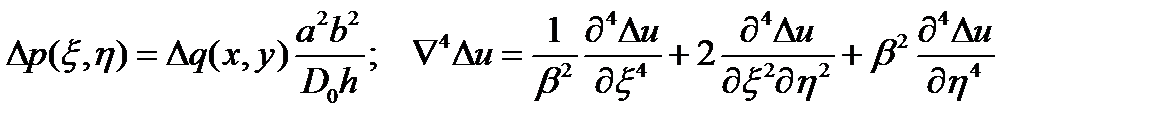

Как видно, из приведенного выше уравнения для изгиба пластинки из нелинейно-деформируемого материала, требуется получить производные от переменной жесткости пластинки.

Первая производная от переменной жесткости пластинки по безразмерным пространственным координатам:

Вторая производная от переменной жесткости пластинки по безразмерным пространственным координатам:

Смешанная производная от переменной жесткости пластинки по безразмерным пространственным координатам:

 

 

Подставляем полученные выше выражения для производных от переменной жесткости в уравнение изгиба пластинки:

2. На втором этапе расчета необходимо определиться с построением и представлением функции аппроксимирующей прогиб и приращение прогиба пластинки из нелинейно-деформируемого материала. В данном случае представим прогиб и приращение прогиба пластинки в виде ряда с конечным числом членов: , где искомые постоянные будем называть обобщенными координатами, а будем называть приращениями обобщенных координат, а функцию - аппроксимирующей (координатной) функцией (функцией, приближающей решение к точному).

 

3. На третьем этапе алгоритма расчета условимся, что будем решать данную задачу в первом приближении метода Бубнова-Галеркина в инкрементальной форме, то есть u (ξ, η) =Ku₁ (ξ) u₂ (η) и Δ u (ξ, η) =ΔKu₁ (ξ) u₂ (η).

Записываем уравнение метода Бубнова-Галеркина, которое будет выглядеть следующим образом:

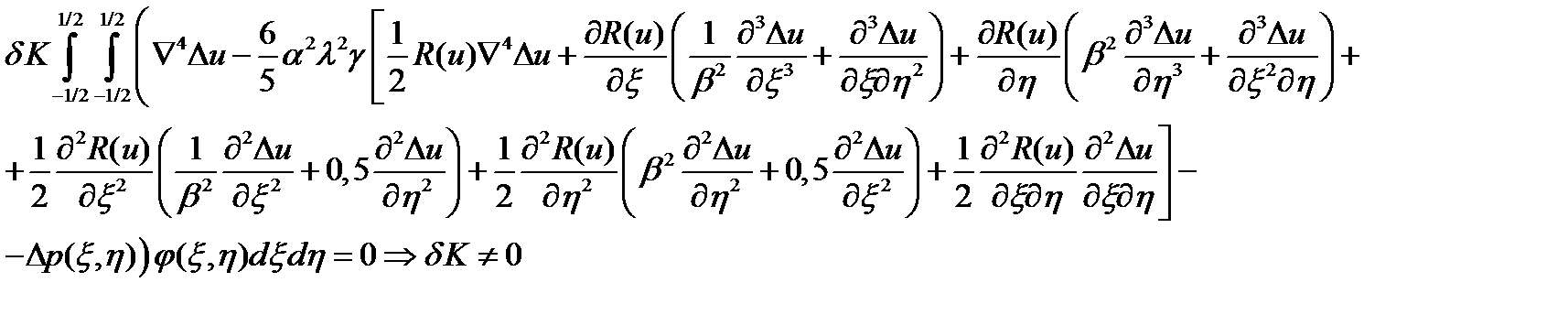
При удовлетворении условий получаем:

 

При подстановке в полученное выше уравнение метода Бубнова-Галеркина выражений для прогибов и приращений прогибов получим следующее:

Квадратичная функция прогиба пластинки:

Бигармонический оператор Лапласа:

Разделим уравнение метода Бубнова-Галеркина на отдельные интегралы:

В результате получим уравнение метода Бубнова-Галеркина в виде:

Коэффициенты которого равны:

 

Приведение коэффициента f₂ к упрощенному виду:

Численная реализация полученных аналитических выражений

Исходные данные для пластинки:

Функция аппроксимирующая прогиб пластинки:

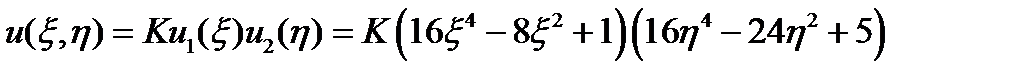
Определение обобщенной координаты K:

 

⇐ Предыдущая123

Поделиться:

Воспользуйтесь поиском по сайту: