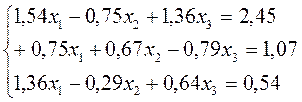|
Мастер функций. Вложенные функции
|
|
|
|
Таблица 2.2
Варианты индивидуальных заданий №1
| № | Функция и проверочные данные | |||
| 1 | 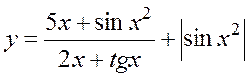
| |||
| При х =2 y (x)= 5,8496 | ||||
| 2 | 
| |||
| При х =2 y (x)= - 0,6354 | ||||
| 3 | 
| |||
| При х1 =2, х2=2 y (x) = 0,1158 | ||||
| 4
| 
| |||
| При х =2 y (x)=6,028 | ||||
| 5 | 
| |||
| При х1 =2 и х2 =2 y (х1, х2) = - 1,7147 | ||||
| 6 | 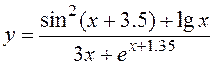
| |||
| При х =2, y (x) =0,0232 | ||||
| 7 | 
| |||
| При х1 =2 и х2 =2 y (х1, х2) =46,9482 | ||||
| 8 | 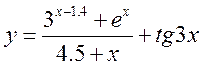
| |||
| При х =2, y (x)=1,1432 | ||||
| 9 | 
| |||
| При х1 =2 и х2 =2 y (х1, х2) =6,022 | ||||
| 10 | 
| |||
| При х =2 y (x)= 9,6488 | ||||
| 11 | 
| |||
| При х =2 y (x)= 0,5693 | ||||
| 12 | 
| |||
| При х1 =2 и х2 =2 y (х1, х2) =7,5196 | ||||
| 13
| 
| |||
| При х =2 y (x) =6,3159 | ||||
| 14 |
| |||
| При х =2 y (x) =5,8045 | ||||
| 15 | 
| |||
| При х =2 y (x)= 2,0480 | ||||
| 16 | 
| |||
| При х =2 y (x)= 0,0694 | ||||
| 17 | 
| |||
| При х1 =2 и х2 =2 y (х1, х2) =3,7921 | ||||
| 18 | 
| |||
| При х1 =2 и х2 =2 y (x)= - 12,2259 |
Таблица 2.3
Варианты индивидуальных заданий №2
| № | Функция и проверочные данные |
| 1 | 
|
| При x=14,26, y= - 1,22, z=0,035 t=0,564846 | |

| |
| При x= - 4,5, y=0,000075, z=84,5 u= - 55,6848 | |
| 2 | 
|
| При x=0,0374, y= - 0,825, z=16 c=1,05534 | |

| |
| При x=4000, y= - 0,875, z= - 0,000475 w =1,98727 | |
| 3 | 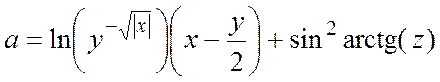
|
| При x= - 15,246, y=0,04642, z=2000,1 a= - 182,036 | |
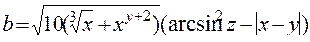
| |
| При x=0,01655, y= - 2,75, z=0,15 b= - 40,6307 | |
| 4 | 
|
| При x=0,1722, y=6,33, z=0,000325 d= - 205,3056 | |

| |
| При x= - 0,02235, y=2,23, z=15,221 d=39,374 | |
| 5 | 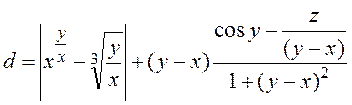
|
| При x=182,5, y=18,225, z= - 0,03298 d=1,2131 | |

| |
| При x=0,03981, y= -1625, z=0,512 a =1,26185 | |
| 6 | 
|
| При x=6,251, y=0,827, z=25,001 b =0,7121 | |

| |
| При x=3,251, y=0,325, z=0,0000466 c =4,2482 | |
| 7 | 
|
| При x=17,421, y=0,010365, z=82800 c =0,33056 | |

| |
| При x=1,23, y=15,4, z=252 g =82,8257 | |
| 8
| 
|
При x=2,444, y=0,00869, z= - 130  - 0,49871 - 0,49871
| |

| |
| При x=14,26, y= - 1,22, z=0,035 t=0,56485 | |
| 9 | 
|
| При x= - 4,5, y=0,000075, z=84,5 u= - 55,6848 | |

| |
| При x=0,0374, y= - 0,825, z=16, c=1,05534 | |
| 10 | 
|
| При x=4000, y= - 0,875, z= - 0,000475 w =1,98727 | |
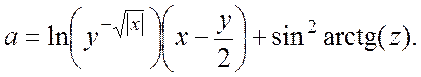
| |
| При x= - 15,246, y=0,04642, z=2000,1 a= - 182,036 | |
| 11 | 
|
| При x=0,01655, y= -2,75, z=0,15 b= - 40,6307 | |

| |
| При x=0,1722, y=6,33, z=0,000325 d= - 205,3056 | |
| 12 | 
|
| При x= - 0,02235, y=2,23, z=15,221 d=39,374 | |

| |
| При x=182,5, y=18,225, z= - 0,03298 d=1,2131 | |
| 13 | 
|
| При x=0,03981, y= -1625, z=0,512 a =1,26185 | |

| |
| При x=6,251, y=0,827, z=25,001 b =0,7121 | |
| 14 | 
|
| При x=3,251, y=0,325, z=0,0000466 c =4,2482 | |

| |
| При x=17,421, y=0,010365, z=82800 c =0,33056 | |
| 15 | 
|
| При x=1,23, y=15,4, z=252 g =82,8257 | |

| |
При x=2,444, y=0,00869, z= - 130  - 0,49871 - 0,49871
|
|
|
|
Пример выполнения задания

Рис. 2.5. Пример выполнения заданий
Математические записи формул и формулы на листах Excel
|
=(5*A10+A10^2)/(4*A10+5*TAN(A10)+6)+ABS(SIN(A10^2)),
где А10 – координата значения х;

=(ABS(COS(A19)-OS(B19)))^(1+2*SIN(B19)^2)*(1+C19^2/2+C19^4/4),
где A19 – x, B19 – y, C19 – z.
TAN, ABS, SIN, COS – функции категории Математические.
Задание 3
Использование математических и логических функций для
Вычисления значений на листах MS Excel
1. Повторить материал теоретической части и изучить раздел справки MS Excel «Создание и проверка формул в книгах».
2. Рассчитать значения функций из таблицы:
3. Значения c и d ввести в ячейки и в формулах использовать их адреса.
4. Рассчитать отдельно значение каждой ветви функции Y(x) на указанных промежутках c шагом h (Y1, Y2, Y3).
5. Рассчитать значение функции Y(x) с использованием логических и математических функций.
6. Сравнить значения функций (п. 2.2 и 2.3) на соответствующих промежутках.
7. Построить график функции Y (x) на промежутке a<=x<=b, h шаг изменения x (по данным п. 3).
Рассчитать значения функции Y(x) на заданном промежутке,
где a <= x <= b, h – шаг изменения x. Значения с, d задать самостоятельно.
Таблица 2.4
Варианты индивидуальных заданий
| 1 |  a=1, b=6, h=0,5
a=1, b=6, h=0,5
| 9 |  a= -3, b=5, h=0,5
a= -3, b=5, h=0,5
|
| 2 |  a=1, b=4p, h=0,2p
a=1, b=4p, h=0,2p
| 10 | 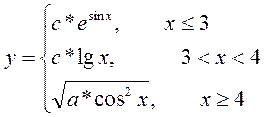 a=1, b=5, h=0,25
a=1, b=5, h=0,25
|
| 3 |  a=-2, b=3, h=0,5
a=-2, b=3, h=0,5
| 11 | 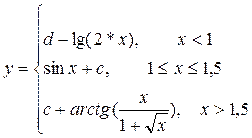 a=0,5, b=2, h=0,2
a=0,5, b=2, h=0,2
|
| 4 |  a=0, b=9, h=0,5
a=0, b=9, h=0,5
| 12 | 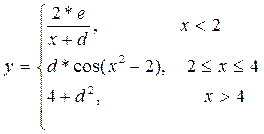 a=0, b=10, h=0,5
a=0, b=10, h=0,5
|
| 5 |  a=1, b=5, h=0,5
a=1, b=5, h=0,5
| 13 |  a=1, b=5, h=0,25
a=1, b=5, h=0,25
|
| 6 | 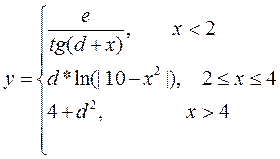 a=1, b=6, h=0,5
a=1, b=6, h=0,5
| 14 |  a=0, b=6, h=0,5
a=0, b=6, h=0,5
|
| 7 |  a=0, b=8, h=0,5
a=0, b=8, h=0,5
| 15 |  a=1, b=6, h=0,5
a=1, b=6, h=0,5
|
| 8 |  a=0,5, b=2p, h=0,1p.
a=0,5, b=2p, h=0,1p.
| 16 |  a=1, b=5, h=0,25
a=1, b=5, h=0,25
|
Пример выполнения задания
Рассчитать значения функции Y(x) на заданном промежутке,
где a <= x <= b, h – шаг изменения x.
Значение d задать самостоятельно как константу.
Построить график функции Y (x).
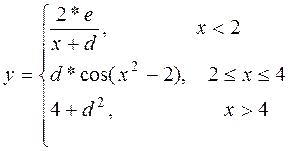
a=0, b=8, h=0,5
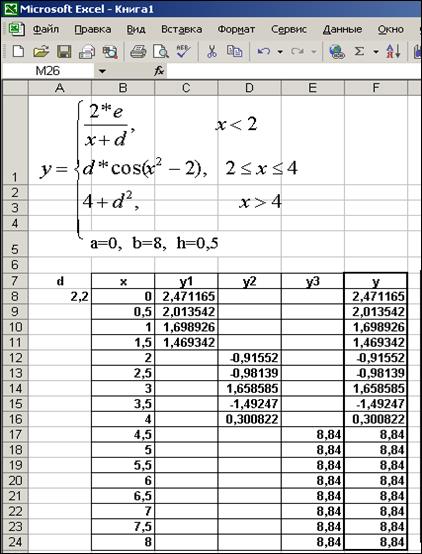
Рис. 2.6. Математические записи формул и вид формул на листах Excel

Рис. 2.7. Лист Excel c формулами
Ячейки C 8, D 8, E 8, F 8 содержат следующие формулы:
| C8 | =2*EXP(1)/(B8+$A$8) |
| D8 | =$A$8*COS(B12^2-2) |
| E8 | =4+$A$8^2 |
| F8 | = ЕСЛИ (B8<2;2*EXP(1)/(B8+$A$8); ЕСЛИ (B8<=4;$A$8*COS(B8^2-2);4+$A$8^2)) |
$ A $8 – координата константы d (абсолютная ссылка).
|
|
|
ЕСЛИ – функция категории Логические, остальные функции категории – М атематические Мастера функций.

Рис. 2.8. Лист Excel c диаграммой
Задание 4
Мастер функций. Работа с массивами и векторами. Функции МОБР, МУМНОЖ, МОПРЕД, ПРОСМОТР
Решить систему линейных уравнений двумя методами: методом Крамера, методом обратной матрицы.
Линейная система называется невырожденной, если определитель отличен от нуля (D ¹ 0).
Невырожденная линейная система имеет единственное решение.
Метод Крамера
х1=1/ D, х2= D 2/ D, …, xn= D n/ D,
где D – общий определитель;
D n (n=1, 2, 3, …, n) соответствующие частные определители.
1. Рассчитать общий и частные определители системы уравнений (для расчетов использовать матричную функцию МОПРЕД).
2. Рассчитать значения переменных х1, х2, х3.
Метод обратной матрицы
1. Составить матрицу из коэффициентов xn системы уравнений.
2. Найти обратную матрицу.
3. Значения переменных х1, х2, х3,… xn – результат умножения обратной матрицы на матрицу, составленную из свободных членов системы уравнений (матрица-столбец).
Замечание.
При вводе функции массива Microsoft Excel автоматически заключает ее в фигурные скобки { }.
Если функция массива возвращает одно значение, укажите ячейку, в которую необходимо ввести формулу.
Если функции массива возвращает несколько значений:
1. Выделите диапазон ячеек, в которые необходимо ввести функцию.
2. Наберите формулу.
3. Нажмите клавиши CTRL + SHIFT + ENTER (т. е. при заранее нажатых клавишах CTRL и SHIFT нажать один раз клавишу ENTER).
Таблица 2.5
Варианты индивидуальных заданий
| № варианта | Система уравнений | |
| 1 | 
| |
| 2 | 
| |
| 3 | 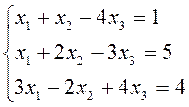
| |
| 4 | 
| |
| 5 | 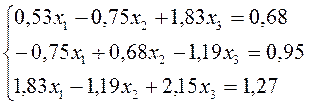
| |
| 6 | 
| |
| 7 | 
| |
| 8 | 
| |
| 9 | 
| |
| 10 | 
| |
| 11 |
| |
| 12 |
| |
| 13 |
| |
| 14 |
| |
| 15 |
| |
| 16 |
| |
Пример выполнения задания

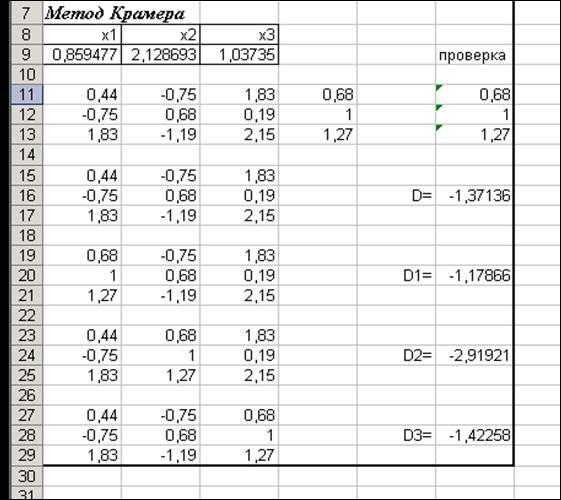
Рис. 2.9. Общий и частные определители системы по методу Крамера

Рис. 2.10. Реализация метода обратной матрицы
Задание 5
|
|
|