Основы классификации экономико-математических моделей с точки зрения характера их применения

Модель

Под моделью подразумевается отображение каким-либо способом процессов, происходящих в реальном объекте. Если эти процессы опи­сываются с помощью математических символов, формул и теорем, то такая модель называется математической.

Рассмотрим, каким образом строится экономико-математичес­кая модель сложной системы. На рис. 1.1.1 показана схема модели сложной системы.

 

		СИСТЕМА
Внешняя среда	X1 X2	α 1, α 2.. z 1, z2 … z η	α k	Y1 Y2 h^ i^	Внешняя среда
	Хп			Y m

Рис. 1.1.1. Схема модели сложной системы

 

Элементы Х_х, Х₂,..., Х_п называются входами системы (входными переменными); Y 1, Y 2,..., Y_m — выходами системы (выходными переменными); Z1, Z_2;..., Zη, характеризуют состояние системы. Ин­дексами α1,α2, …α k обозначены параметры системы. Входы и вы­ходы осуществляют связь системы с внешней средой, т.е. другими системами. Элементы Z1, Z2,..., Z_η фиксируют все изменения состо­яния системы, происходящие за счет поступления входных сигналов и вследствие внутренних процессов, протекающих в ней.

Допустим, необходимо построить модель предприятия, выпуска­ющего велосипеды. Представим предприятие в виде системы и по­строим ее модель. В качестве входов системы можно принять такие переменные: X1 — поставки сырья для производства велосипедов; Х2 — поставки оборудования; Х₃ — поток людей, нанимающихся на работу; Х₄ — план выпуска продукции и т.п. Состояниями такой системы можно назвать: Z1 — текущее время; Z2 — дефицит обо­рудования; Z₃ — соответствие фактической численности работаю­щих нормативной; Z₄ — степень выполнения плана на текущий мо­мент и т.п. Параметры системы α1, а2,...,α k могут характеризовать всевозможные нормы и нормативы, принятые для данного предпри

ятия. Выходы системы отображают результаты ее функционирования и могут представлять собой следующие величины: Y1 количество выпущенной продукции; Y2 ее стоимость; Y3 - про­изводительность труда; Y₄ - размер полученной прибыли и другие показатели деятельности предприятия.

В конкретных моделях систем входы, выходы и состояния свя­заны между собой функциональными или статистическими зависимостями. Задавая определенные значения входных сигналов, исход­ных параметров и зависимости между переменными, при помощи определенных экономико-математических методов осуществляют исследование модели по интересующим показателям.

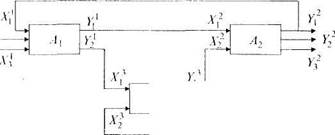
Модели различных систем могут образовывать более крупные и сложные модели. Для этого осуществляют сопряжение отдельных моделей через их входы и выходы (рис. 1.1.2).

j—■—I >'з3

AV

 

 

Рис. 1.1.2. Соединение трех моделей систем в одну

Соединение моделей между собой задается при помощи опера­торов сопряжений, которые указывают на наличие или отсутствие связей между отдельными входами и выходами. Запишем оператор сопряжения для модели, изображенной па рис. 1.1.2. Он представлен в матричной форме (табл. 1.1.1). При наличии связей между входами и выходами в матрице проставляется цифра 1, в противном случае клетка матрицы остается пустой. Любую совокупность моделей сис­тем, сопряженных друг с другом, можно представить в виде одной модели системы с новыми наборами входов, выходов, состояний и параметров.

 

Таблица

Оператор сопряжения

 

Вход	Выход
	Y1¹	Y 2 ¹	Y1 ²	Y2 ²	Y3²	Y 1³	Y2³	Y3³
X 1 ¹
X 2¹
X 3 ¹
X 1² ²
X 2 ²
X 1 ³
X 2 ³

Функционирование системы во времени характеризуется появле­нием входных, выходных сигналов и изменением состояний в век­торных пространствах входных, выходных сигналов и состояний.

Под пространством сигналов или состояний понимают п-мерное векторное пространство типа

 

А=А1*А2* …*Аγ* …* Аn, γ = 1,n

Точка в пространстве соответствует конкретному значению сиг­налу или состояния. Так, если имеется, пространство состояний

Z = Z1 х Z₂ х... х ZyX... х Z_n где Zy e Z — ось пространства, то

конкретное состояние системы задается координатами точки Z < Z в пространстве состояний. Координатами точки Z в пространстве Z являются проекции пой точки па все оси пространства, т.е. Z = (Z1, Z 2|,…, Zn)

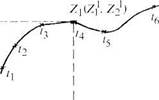
Частными случаями пространств сигналов и состояний являются двумерное и трехмерное пространства. Наиболее наглядно можно представить двумерное пространство. На рис. 1.1.3 показаны состо­яния некоторой системы в пространстве состояний.

Последовательность состояний системы в различные моменты времени t1, t2, …tn называется траекторией ее движения. Траекто­рия системы показывает изменение се состояния во времени.

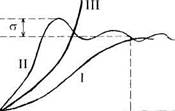
Реакция системы на какой-либо входной сигнал или внутреннее изменение называется переходным процессом. Понятие переходного процесса можно применять как к состояниям, так и к выходам сис­темы. Поскольку при моделировании нас интересуют значения вы­ходов системы, то чаще переходный процесс системы относят к вы­ходным сигналам. Переходные процессы систем изображены на рис. 1.1.4. Они характеризуются продолжительностью Т, величиной перерегулирования σ (максимальным отклонением У от Y0 за время переходного процесса), величиной колебательности переходного про­цесса £ (коэффициентом демпфирования) и т.п. Переходный про­цесс — это показатель функционирования системы во времени, ука­зывающий, как быстро и в какое новое состояние она перейдет в результате появления входного сигнала или внутреннего изменения. Система находится в равновесии, если ее состояние остается неиз­менным неограниченное время. У системы может быть несколько со­стояний равновесия. Если система переходит из одного состояния равновесия в другое под действием входных сигналов или внутренних причин, то она называется устойчивой. На рис. 1.1.4 переходные про­цессы I и II соответствуют устойчивой системе, а процесс III не­устойчивой.

Как правило, все системы, которые подлежат моделированию, являются устойчивыми.

 

7,\ Z₂

Рис. 1.1.3. Пространство состояний системы

Y

 

 

Т

 

Рис. 1.1.4. Переходные процессы систем

 

Управление и моделирование

Под управлением системами будем понимать процесс, ориенти­рующий некоторую систему на достижение определенной цели. По­нятие управления имеет двоякое содержание: управление как управ­ленческая деятельность и управление как процесс.

При рассмотрении управления как управленческой деятельности обычно существуют объект управления и управляющий орган. Уп­равленческая деятельность управляющего органа сводится к опре­делению цели управления, методов и средств ее достижения, поста­новке задач управления, выбору исполнителей, постоянному кон­тролю.

Понятие управления как управленческой деятельности состоит в конкретном содержательном отношении субъекта к объекту управ­ления. Так, например, директор предприятия, осуществляя управ­ленческую деятельность, должен хорошо знать экономику, технику, технологию производства, людей, с которыми работает, ясно пред­ставлять свои перспективные цели и цели на отдельных этапах, знать законы.

Управление как процесс рассматривается независимо от конкрет­ных характеристик объекта и субъекта. В этом случае управление сводится к определению параметров процесса управления и иссле­дованию структурных особенностей процесса, последовательности его этапов. При такой трактовке управления обычно выделяют уп­равляющую и управляемую подсистемы.

Понятие управления как процесса дает возможность управлять, не познавая полностью объект управления. Например, можно, не зная устройства автомобиля, научиться им управлять; можно на­строить телевизор, не имея представления о его конструкции. Здесь налицо функциональный подход к управлению. Различие двух по­нятий управления наглядно проявляется при принятии решений. Если управление рассматривается как процесс, то принятие решения сводится к выбору одного из вариантов управления, оптимального, по заранее заданному критерию. Критерий в данном случае не яв­ляется предметом принятия решения. При рассмотрении управления как управленческой деятельности субъект управления должен сам вырабатывать критерии и цели управления, корректировать их в процессе управления. В этом смысле управление как деятельность более широкое понятие, чем управление как процесс. Управленчес­кая деятельность в целом гораздо менее формализуемое явление.

При экономико-математическом моделировании используются оба понятия управления, так как объектами исследования являются социально-экономические системы. Однако применение конкретных математических методов возможно только для объектов, имеющих определенную, заранее заданную цель функционирования. Экономи­ко-математическое моделирование не занимается выработкой целей экономических объектов. Это сфера деятельности политической эко­номии и конкретных экономических наук. Экономико-математичес­кие методы определяют наилучшие пуги управления системой для достижения заданной цели системы. Таким образом, управление при экономико-математическом моделировании следует понимать ис­ключительно как управление процессами. Управление в виде управ­ленческой деятельности тоже присутствует в социально-экономичес­ких системах, так как они содержат в себе в качестве подсистем кол­лективы, вырабатывающие определенные цели. Но эти коллективы, или подсистемы субъектов, отражающие объективную реальность и вырабатывающие определенные суждения и цели функционирова­ния социально-экономических систем, базируются в своей деятель­ности на принципиально иных категориях и поэтому не могут быть полностью формализованы в виде экономико-математических моде­лей.

Модель социально-экономичес­кого объекта, способного выраба­тывать и корректировать цели свое­го функционирования, можно представить как обычную систему с до­полнительными управляющими входами (рис. 1.1.5).

Рис. 1.1.5. Модель системы с корректируемыми целями

Управляющие входы, g1, g2..., gj предназначены для изменения цели функционирования системы, которое может произойти только из внешней для данной системы среды.

Всякое управление в таких системах осуществляется как инфор­мационный процесс: получение, обработка и передача информации. Изменение состояния системы в результате управления происходит па основе получения информации (поступления входных сигналов) и является реакцией на команду, которая вырабатывается в системе после анализа информации, содержащейся во входном сигнале.

 

 

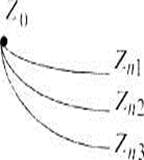
Изменение состояния системы в результате управления показано на рис. 1.1.6. Здесь Z₀ — исходное со­стояние системы, a Zn1, Z_;n2, Z_n3 — ее новые состояния, полученные при различной интенсивности уп­равляющего сигнала.

Рис. 1.1.6. Изменение состояния системы при различной интенсивности управляющего сигнала

Управление системой нераз­рывно связано с понятием цели уп­равления системой или просто цели системы. Под целью управления сис­темой понимают определенное желаемое значение ее выходов при ус­ловии, что они в достаточной мере отражают состояние системы. Цель это своеобразный эталон функционирования системы. При моделировании цель системы представляется в виде целевой функ­ции - математического выражения связей входов и выходов систе­мы друг с другом, отражающего поведение системы с точки зрения целевой установки.

Цель системы -- идеализированное понятие. Обычно выходные сигналы или состояния системы находятся вблизи своих целевых значений или колеблются около них. Чтобы оценить степень при­ближения системы к ее цели, вводят понятие критерия достижения цели или критерия цели.

Критерием цели назовем правило, позволяющее оценить фактичес­кое поведение системы (состояние входов, значение целевой функции) в сравнении с желаемым, целевым, поведением и зафиксировать до­статочность или недостаточность этой оценки. По критерию цели отбирают оптимальный вариант поведения системы, в наибольшей степени отвечающий цели системы. Обычно критерии задают в виде минимума (максимума) целевой функции или значений выходов сис­темы, однако это всего лишь частный случай. Существует достаточ­но большое число математических имитационных методов, которые позволяют существенно расширить возможности задания целевых функций и критериев целей.

Построение целевых функций систем является одной из важней­ших задач экономико-математического моделирования. Рассмотрим основные принципиальные положения определения целевых функ­ций систем.

Принцип однозначности требует наличия единственной целевой функции системы. Если в системе имеется несколько частных целевых функций А1, А₂,… Аа, то их следует объединить в одну посред­ством какой-либо комбинации, например

А=А1К₁ + А₂К₂+... + А_аК_а

где А - обобщенная целевая функция системы;

Kj коэффициенты относительной важности частных целевых функций, ј = 1, а.

Принцип управляемости выражает необходимость зависимости целевой функции от параметров управления системой (входных сиг­налов).

Принцип подходящей формы заключается в установлении такой формы целевой функции, при которой она имела бы практический смысл, экстремальность (т.е. обеспечивала получение максимума или минимума) и была бы однозначной.

В практических задачах встречается большое разнообразие типов целевых функций. Рассмотрим наиболее употребимые. Целе­вую функцию прибыли обычно задают в следующем виде:

F=∑Uί Vί - ∑ Cј Pј

ί ј

где U_ί — цена ί-го вида продукции;

Vί — объем выпуска ί-го вида продукции;

Сј — стоимость единицы ј-го типа ресурса, израсходованного на изготовление продукции;

Рј — потребная величина ј'-го типа ресурса.

Выбор целевой функции такого вида позволяет обеспечить мак­симальную положительную разницу между объемом реализованной продукции и величиной затрат ресурсов, использованных для ее из­готовления, т.е. максимальную прибыль.

Целевая функция себестоимости имеет вид

 

F = ∑ Cί (X k),

где Х_k — к-й фактор, влияющий на себестоимость. Эта целевая функция отражает стоимость, связанную с осуществлением процесса производства. Обычно под переменными Х_k понимают стоимость факторов, поддающихся управлению (стоимость материалов, топли­ва и т.п.), а функцию F минимизируют.

Целевую функцию качества некоторого процесса задают в виде квадратичной формы

 

F = ∑ ψј (Yј – Yј)²

где Y ј – требуемое значение качества ј-го параметра:

Yj фактическое значение качества ј-го параметра;

Ψј - положительный весовой коэффициент ј-го napaметpa.

Данная целевая функция качества обеспечивает минимизациию взвешенной суммы квадратов отклонений всех параметров от их требуемых значений.

Целевая функции времени выражает стремление минимизировать продолжи тельность процесса между двумя фиксированными граничными условиями и может быть записана в виде

t∫

Т = min ∫ dt

t0.

Понятие обратной связи лежит в основе большинства процессов управления и является фундаментальным. Что такое обратная связь?

 

Рис. 1.1.7. Модель cue темы с обра тной связью

В формальном представлении с пози­ции системы обратная связь, означает получение информации о результате управления. Выходной сигнал систе­мы, несущий информацию о ее состо­янии, должен поступить на ее вход. На рис. 1.1.7 представлена модель системы с обратной связью, осущест­вляемой через некоторый управляю­щий орган УО.

Приведем несколько примеров систем с обратной связью. Чтобы взять какой-либо предмет, человек протягивает руку, гла­зами следит за ее положением в пространстве и непрерывно управ­ляем движением руки относительно предмета, исправляя ошибки на­правления ее движения. Здесь налицо система «человек - пред­мет - зрительная обратная связь - глаза - рука (через управляю­щий opган) - мозг».

В качестве систем с обратной связью можно представить про­цессы производства товаром и услуг. Через величину спроса рынок будет регулировать необходимый объем производства товаров или предоставления услуг.

Обратная связь в системах может быть отрицательной и поло­жительной.

Отрицательная обратная связь характеризуется тем, что выход­ной сигнал, воздействующий на вход системы, имеет противоположный знак по отношению к входному, вызвавшему изменение состо­яния системы. Тем самым он нейтрализует в определенной степени входной сигнал. Отрицательная обратная связь обычно предназна­чена для поддержания системы в определенном устойчивом состоя­нии. Так, например, при поддержании постоянного уровня производства и потребления используются различные механизмы отрицательной обратной связи.

Положительная обратная связь характеризуется тем, что выход­ной сигнал, подаваемый в качестве сигнала обратной связи на вход, имеет одинаковый знак с входным сигналом и поэтому усиливает его действие. Системы с положительной обратной связью являются неустойчивыми. Они обычно находятся в стадии развития или ги­бели.

Типы управления. На практике встречается несколько чипов уп­равления системами: жесткое (без обратной связи), с обратной свя­зью, адаптивное.

Жесткое управление, или управление без обратной связи, явля­ется простейшим. В этом случае система полностью зависит от про­граммы изменения входного управляющего сигнала. Такой вид уп­равления применяется, когда зависимость изменения выходного сиг­нала от входного является известной и действие помех на систему не приводит к существенным искажениям ее выходных характерис­тик. Примерами жесткого управления могут служить управление то­карным станком, автомобильным движением при помощи светофо­ра, работа ЭВМ по заданной программе и пр.

Управление с обратной связью - наиболее распространенный тип управления, рассмотренный выше.

Адаптивное управление также является управлением с обратной связью и отличается от последнего наличием специального адаптив­ного (приспособительного) механизма, накапливающего и анализи­рующего информацию о прошлых управленческих ситуациях, выра­батывающего новую линию поведения на основе прошлого опыта в соответствии с заложенными целями и критериями.

Адаптивное управление присуще сложным системам, которым в процессе функционирования приходится изменять программы и стратегии поведения за счет обучения. Теория адаптивного управ­ления пока не получила большого развития, как, например, теория споем с обратной связью, вследствие чрезвычайной сложности фор­мирования принципов обучения.

Итак, мы рассмотрели наиболее важные понятия и идеи, исполь­зуемые при моделировании социально-экономических объектов. За­метим, что категории «организация», «система», «структура» и связанные с ними понятия легко поддаются формальному математичес­кому описанию.

 

Основы классификации экономико-математических моделей с точки зрения характера их применения

 

Экономико-математическая модель представляет собой отобра­жение некоторых процессов, протекающих в моделируемом объекте, при помощи математических символов, уравнений, теорем. Естест­венно, всякая модель — всего лишь упрощенный образ объекта ис­следования, наиболее полно отражающий те черты объекта, кото­рые интересуют исследователя. Например, если цель моделирования производственного предприятия — совершенствование производст­венного процесса, то наиболее точного и адекватного отображения требуют процессы движения материалов, полуфабрикатов, готовых узлов изделия, последовательность их обработки, сборки, ритмы движения конвейеров, процессы взаимного согласования производ­ственных планов, календарные планы, графики и т.п. Обработка учетной информации, начисление заработной платы, расчет основ­ных показателей работы предприятия, а также информационные связи между подразделениями аппарата управления не имеют особого значения при моделировании непосредственно производствен­ного процесса и, как правило, либо вообще отсутствуют в его мо­дели, либо присутствуют в виде констант или исходных данных.

Наоборот, если цель моделирования — совершенствование ап­парата управления предприятием, то основным объектом моделиро­вания являются информационные потоки, существующие в аппарате управления, методика их обработки и преобразования, процессы принятия управленческих решений.

Таким образом, экономико-математическая модель объекта ото­бражает наиболее полно и точно только те черты и свойства объекта моделирования, которые интересуют исследователя.

В зависимости от природы объекта, целей, методов и особеннос­тей его описания экономико-математические модели могут быть классифицированы по целому ряду признаков. Такими признаками являются, например, степень огрубления структуры объекта (модели агрегированные и детализированные); степень огрубления свойств, элементов и структурных отношений моделируемого объекта (моде­ли детерминистские, вероятностные, модели с риском и неопреде­ленностью); глубина охвата структурной организации объекта ис­следования (модели производственно-технологической структуры, модели структуры экономики, модели социальной структуры обще­ства, модели окружающей среды и т.п.); тип изменения переменных

 

 

(модели с непрерывными, дискретными переменными и модели сме­шанного типа) и др.

Детальная классификация экономико-математических моделей по всем возможным основаниям пока отсутствует. Это обусловли­вается наличием разных точек зрения и подходов к экономико-ма­тематическому моделированию, отставанием философско-методологического осмысления новой области знаний.

Для экономистов, финансистов и менеджеров особый интерес представляет классификация моделей по характеру их использова­ния. Попытаемся условно расчленить экономико-математические модели по возможности их применения в той или иной ситуации на конкретных примерах. Здесь принято [13] деление моделей на четыре класса: модели без управления, оптимизационные, игровые и ими­тационные.

 

Модели без управления

 

Экономико-математические модели без управления (дескриптив­ные модели) представляют собой в основном статистические модели (кривые роста, регрессионные линии), предназначенные для иссле­дования объектов путем установления количественных соотношений между их характеристиками или параметрами.

Например, требуется определить зависимость потребления бы­товых услуг от уровня доходов населения, обеспеченности бытовы­ми предметами на душу населения и других факторов потребления. Для этого составляют регрессионное уравнение

Y= a0 + a1x1+ a2x2 + … + a nx n,

где Y — потребление бытовых услуг на душу населения;

, х₂,..., х_п — факторы потребления;

а₀, a1,..., аn_п — коэффициенты уравнения.

Если известны коэффициенты а₀, a1,..., а_п, то зависимость по­требления бытовых услуг от принятых факторов считается опреде­ленной. Она отражает реальную ситуацию только в среднем, или в статистическом смысле.

Приведем другой пример модели без управления. Требуется оп­ределить количество заместителей директора для типовых структур управления предприятием. В этом случае проводят статистическое исследование численности указанной категории работников на су­ществующих предприятиях и выводят степенное уравнение. В частности, при определенной специализации количество заместителей директора Nзам определяют по формуле

_Nзам = 0,0871N nnФ0°^:1,

 

где N_nn — численность промышленного персонала;

Ф_о — основные и оборотные фонды.

Еще один пример. Пусть требуется определить парк предметов бытовой техники у населения в 2000 г. по данным за 1990—1995 гг. Предположим, что зависимость парка предметов бытовой техники от времени можно представить в экспоненциальной форме

r (t-1995)

X (t) = X 0 e

где X{t) — парк бытовых предметов в произвольном году /;

Xq — парк указанных предметов в 1995 г.;

r —.коэффициент роста;

е — основание натурального логарифма (е ~ 2,72).

С помощью приведенной формулы можно составить прогноз о том, сколько будет предметов бытовой техники у населения в 2000 г.:

 

r (2000-1995) 5r

X (200) = X 0 е = X 0 е

 

Подобный подход к прогнозированию парка бытовой техники у населения, конечно, не может обеспечить получение точных ре­зультатов. Он приведен для иллюстрации моделей данного типа, од­нако довольно часто применение аналогичных моделей позволяет изучать важнейшие народнохозяйственные процессы и пропорции.

Модели без управления применяют для изучения фактически су­ществующих процессов, без вмешательства в их течение. Область применения этих моделей достаточно широка. К моделям без управ­ления принадлежат модели экономики страны, расширенного вос­производства, прогнозирования рождаемости, численности населе­ния и т.д. Как правило, они дают общее представление об объекте. Процессы в моделируемом объекте отображаются в агрегированном виде и максимально обобщены. Поэтому модели без управления не дают полного представления об объекте моделирования и пригодны для изучения только самых общих изменений и тенденций.

Построение достаточно хороших моделей без управления требу­ет большого количества специальной информации об объекте моде­лирования. Поэтому для построения моделей такого типа нужно быть специалистом в той области, к которой принадлежит данный объект или процесс моделирования. Одних математических знаний здесь, конечно, недостаточно.

Значимость моделей без управления велика — они позволяют изучать явления в целом, комплексно и устанавливают общие фун­даментальные свойства объектов и процессов.

 

Оптимизационные модели

 

Важный класс моделей образуют оптимизационные модели. Их появление и применение вызвано необходимостью решения практи­ческих задач, возникающих в экономике и технике. Требовалось перевозить грузы с минимальными издержками, правильно выби­рать режимы резания станков, регулировать частоту вращения электродвигателей, обеспечивать полеты самолетов по заданному курсу, раскраивать детали из листовых материалов с минимальными отходами и т.д. Решение таких задач стимулировало становление и развитие теории автоматического управления, теории информации и математического программирования. Постепенно эти научные на­правления расширились, обогатились практическими примерами. Выяснилось, что их можно применять для решения разнообразных задач независимо от их конкретной природы. В дальнейшем учены­ми были высказаны обобщающие идеи, введены основополагающие принципы и термины, которые объединили теорию автоматического управления, теорию информации, теорию систем и некоторые дру­гие научные направления. В результате образовалась новая наука об управлении — кибернетика. Принципы кибернетики стали при­меняться для познания процессов, протекающих в живых организ­мах, социальных и экономических системах.

Использование принципов и идей кибернетики для получения оптимальных решений при управлении производством и экономи­кой привело к появлению многочисленных экономико-математичес­ких оптимизационных моделей. Варианты планов экономического развития, полученные на основе построения таких моделей, как пра­вило, оказывались лучше интуитивных. Схемы рационального раз­мещения производительных сил, соответствующие оптимальным ре­шениям, обеспечивают существенную экономию затрат, более эф­фективное использование имеющихся ресурсов.

Особенностью оптимизационных моделей является целенаправ­ленность решения и явная оценка эффективности (качества) различ­ных вариантов решения. В отличие от моделей без управления оп­тимизационные модели предполагают выявление цели управления и построение целевой функции. Целевая функция, как упоминалось ранее, задает желаемые значения определенных параметров (свойств, выходов) системы или процесса, выраженные в математи­ческой форме.

Суть получения оптимального решения на модели заключается в следующем. Допустим, что известна цель управления (целевая функция), она может быть достигнута при разных значениях пара­метров данного объекта или различных вариантах решения и име­ется возможность оценить эффективность (степень достижения цели) каждого варианта. Тогда получение оптимального решения означа­ет выбор из множества возможных решений одного, обеспечиваю­щего максимальную эффективность.

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: