 |
Концептуальная модель задачи «Рейтинг» обучаемого
|
|
|
|
ОБЩАЯ ТЕОРИЯ СИСТЕМ
Методические указания предназначены
для студентов специальности 080500.62.01
«Архитектура предприятия»
Москва 2012
Составитель В.М. Панченко, А.И. Комаров
Редактор Панов А.И.
Общая теория систем (ОТС) является методологической основой решения проблемных творческих задач, связанных с изучением и моделированием процессов поведения реальных объектов. Методические указания предназначены для студентов специальности 080500.62.01 «Архитектура предприятия»
Форматирование, компоновка, компьютерная верстка и отработка программы единичного эксперимента по применению методических указаний в учебном процессе реализована аспирантом кафедры Антроповым В.А.
Печатается по решению редакционно-издательского совета университета.
Рецензенты: Свиридов А.П.,
Холкин И.И.
© МГТУ МИРЭА, 2012
ВЕДЕНИЕ
Дисциплина "Общая теория систем" (ОТС) - это самостоятельный раздел учебного плана подготовки специалистов на факультете экономики и управления (ФЭиУ) МИРЭА направления подготовки 080050062 «Бизнес-информатика» по профилю подготовки «Архитектура предприятия».
Теория систем является методологической базой для проявления на деле компетентности индивидуума, активации его творческого потенциала при решении системообразующих задач. Следовательно, ОТС является необходимым условием к постановке и решению творческих задач. Она способствует росту общей системной компетентности специалиста, проявляемой в процессе предметно-познавательной деятельности
Особый интерес представляет объединение системообразующих научных дисциплин на основе общей теории систем (системологии) и системного анализа
|
|
|
1. ЦЕЛИ И ЗАДАЧИ ОСВОЕНИЯ ДИСЦИПЛИНЫ
1.1. Целями освоения дисциплины (модуля Б.2.Б.08 учебного плана) являются:
Создание теоретической и практической основы для формализованного описания реальных объектов и их систем, построенного на принципе системного подхода и последующей алгоритмизации расчётов и программирования решений.
Решение профессиональных задач, связанных с формализацией предметной области программного проекта на основе методов, моделей и средств структуралистской концепции интеграции знаний,
Содействие заказчику в оценке и выборе вариантов программного обеспечения при решении формализованных и слабо формализованных задач из практики развития конструктивной общей теории систем....
1.2. Задачи изучения дисциплины связаны с формированием основных понятий эпистемологии, в частности, с теорией организации познавательных процессов, определением уровней рационального и эмпирического (системологического) описания объекта наблюдений, формированием системного описания объекта, как модели для познания и управления реальной системой (объектом наблюдений - «Ъ»).
В результате изучения дисциплины студент должен:
• Иметь представление об основных понятиях познавательного процесса и его организации.
• Знать уровни абстракций возможного рационального и эмпирического представления реальной системы (объекта исследований и проектирования – «Ъ»).
• Уметь строить системное описание как заданной предметной области знаний, так и предметной области деятельности в ней.
• Владеть средствами конкретизации и абстрагирования при конструировании модели объекта наблюдений.
• Сформировать опыт решения задач системологического описания модели реальной системы, процесса или явления на соответствующем решаемой задаче уровне конкретизации - абстрагирования с применением системных технологий общей теории систем.
|
|
|
2. Связь с другими дисциплинами учебного плана
Дисциплина относится к математическому и естественно научному циклу ООП, связана с предметно-аналитической и проективной деятельностью по созданию компонент системного описания объекта и его программного обеспечения, логически и содержательно-методически взаимосвязана с базовыми дисциплинами цикла Б2.
Является основой для формирования моделей дисциплины теория принятия решений и задач вариативной части дисциплин блока Б3.Б.
Особенностью теории систем, которую часто называют эпистемологией (теорией познания), является меж предметный характер изучаемых понятий, методов и моделей, образующих так называемое "второе измерение" в науке, основанное на свойствах различных родов морфизмов (изоморфизмов, гомоморфизмов, эпиморфизмов). В этом смысле эпистемология является методологической дисциплиной, направленной на обобщение знаний и опыта, накопленного в отдельных дисциплинах, независимо от содержательной сущности изучаемых в этих дисциплинах свойств реальных объектов наблюдений.
Процесс интеграции наук на основе общей теории систем весьма многогранен и отвечает тенденции развития теории познания, отмеченной Акоффом Р.А. в виде утверждения: “Нужно перестать поступать так, словно природа делится на дисциплины, как в университетах”.
3. Содержание теоретического курса
3.1. Теория систем и эпистемология
Тема 1.1. Наука о системах. Исходные понятия
эпистемологии. Категории объекта (Ъ)и субъекта (Ь). Системный подход. Операции абстрагирования и конкретизации. История возникновения теории систем. Перспективы развития.
Тема 1.2. Системная парадигма. Роль парадигмы в
познавательном процессе. Изоморфизмы как второе измерение в науке о системах. Отождествление объекта наблюдений с системой. Каналы наблюдений. Онтологические и гносеологические проблемы познавательного процесса. Каналы абстрагирования -конкретизации.
Тема 1.3. Системный анализ и системный подход.
Связь с системным подходом. Уровни классов рациональных и эмпирических систем. Предметные области знаний и деятельности. К формализации определения понятия система. Общая система. Конкретная система, реальная система и система моделей. Основы классификации систем.
|
|
|
3.2. Уровни рациональных систем
Тема 2.1. Знаково-лингвистическое описание системы. Термы. Функторы. Конституэнты. Высказывания. Роль зыка (естественного, ограниченного естественного, формально го, объектного). Объект как кибернетическая система. Черный, серый и белый "ящики". Признаки свойств объекта и среды объекта. Правильное истинное и ложное высказывание. Теория. Система по Месаровичу на знаково-лингвистическом уровне.
Тема 2.2. Теоретико-множественное описание системы. Система правильных высказываний как собственное подмножество. Кортеж, вектор, последовательность и другие элементы множества. Объект в виде точки в n-мерном пространстве. Теоретико-множественное описание объекта. Аксиоматические теории. Интуитивные построения, теоремы Гёделя. Принцип Черча.
Тема 2.3. Абстрактно - алгебраическое описание системы. Математическая структура. Алгебраическая операция. Базовые множества-носители структуры. Примеры абстрактно-алгебраических структур. Свойства отношений вида функции, функционала, оператора. Изоморфизм физических и математических систем. Мультипликативные и аддитивные отношения. Формы представления алгебраических систем.
Тема 2.4. Логико-математический уровень описания систем. Логико-математическая интерпретация алгебраической операции. Логические функции как направленная система. Задача упорядочения на основе логического подхода. Логическая топология. Изоморфизмы логических описаний и систем.
Тема 2.5. Топология и топологические уровни описания систем. Пространства и пространственно-подобные отношения. Свойства пространства. Пространство как математическая структура. Примеры пространств. Топологические пространства. Линейность пространства. Норма и нормирование. Система базирования в пространстве.
Тема 2.6. Информационный уровень конкретизации систем. Информация и топология, топологический подход к описанию по Хартли и К. Шеннону. Аддитивность меры. Двухальтернативный случай выбора и исхода.
|
|
|
Тема 2. 7. Меры нечеткости. Классы систем по мере нечеткости. Оценка нечеткости на примере механизмов случайного выбора. Система механизмов.
Тема 2.8. Динамический уровень описания систем. Свойства времени как особого множества. Системы измерения. Общая динамическая система. Время-подобные отношения для дискретных систем. Пространство состояний и переходов. Математическое состояние динамической системы. Диаграмма преобразований. Автоматы как пример динамической системы.
3.3. Уровни эмпирических систем
Тема 3.1. Исходная эмпирическая система наблюдений. Алгебраическое описание и структура отношений. Каналы наблюдений и абстрагирования. Схема описания объекта на уровне исходной системы. Чёткие и нечёткие каналы наблюдений. Особенности создания исходной системы.
Тема 3.2. Система данных (Д) для эмпирического уровня наблюдений. База и переменная. Система данных как алгебраическая операция.. Данные с семантикой. Модальность семантики порождения. Классы нечетких мер при описании систем данных.
Тема 3.3. Системы порождения. Основные понятия. Примеры порождения и выборки данных. Маска и адресные уравнения. Системы порождения с поведением. Маски выборки. Выборочные переменные.
Тема 3.4. Системы с нечёткими функциями выбора. Задание нечёткой функции выбора. Моделирование поведения. Структура системы с нечеткими элементами выбора. Имитация поведения. Обработка результатов наблюдений..
Тема 3.5. Эпистемология основных уровней эмпирических систем. Упорядоченная система данных. Уровень порождающих систем. Структуризация и метаоперации. Перечисление методологических типов систем эпистемологических уровней.
3.4. Эвристический уровень описания объекта
Тема 4.1. Общая схема уровней рациональных и эмпирических систем. Эвристический уровень. Роль интуиции.
Тема 4.2. Связь теории систем с основами теории творческой деятельности.
Тема 4.3. Перспективы развития теории систем. Системы, построенные на инженерии знаний. Информационные семантические системы.
Тема 4.4. Автоматизированные системы обучения. Роль и место персональной техники и сетевых структур в развитии эпистемологии, науки о теории познания и процессах познания
4. Методические указания по изучению
дисциплины
Основной целью изучения теории систем является междисциплинарный обмен методами, моделями и средствами для организации познавательного процесса на основе пособия и аналогий, как частных представлений понятия изоморфизма. Очевидно, что без интуиции и экспертного обобщения знаний подобный творческий процесс невозможно реализовать.
|
|
|
Из вышеизложенного вытекает, что в качестве объектов изучения для практических, и самостоятельных занятий студентов могут выбираться объекты любой природы.
Желательно при этом в качестве основных объектов изучения использовать объекты информационного типа: тексты, рисунки, таблицы, понятия и их определение, пакеты прикладных программных продуктов, информационные и документальные системы, имеющие семиотическую природу. Для задач искусственного интеллекта основным полигоном исследований служат информационные семантические системы и составляющие их элементы.
С другой стороны, информационная семантическая система всегда связана с описанием объектов различной природы: физической, химической, биологической, социальной, лингвистической... В этом смысле изоморфизм объектов семантической и естественнонаучной природы должен обеспечиваться изначально множеством правильных высказываний.
5. Образовательные технологии
В качестве образовательных технологий (при реализации различных видов учебной работы) предусматривается возможность использования системы последовательного формирования базовой оценки обучаемого по итогам и в процессе выполнения фрагментов рабочей программы курса. С этой целью отработана система файлов, основу которой составляют три папки (ЛПС - личная папка студента; ПУГ - папка учебной группы; ПР - папка репозиторий). К наполнению папок содержанием и интеракивной учебной составляющей привлекаются сами студенты.
Удельный вес занятий, проводимых в интерактивных формах, определяется главной целью данной рабочей программы, учитываются особенности контингента обучающихся и особенности обучения на базе использования компьютерный средств обучения
6. Самостоятельная работа студентов (СРС)
Студенты выполняют индивидуальные задания, связанные с закреплением знаний, умений и навыков (ЗУН) на практике, по схеме. формирования модели объекта наблюдений на основе рационалъных и эмпирических комплексов теории систем.
Особенности и трудности обучения системообразующим понятиям ОТС определяются тем, что согласно учебного плана изучение дисциплины ведётся на первом семестре первого года обучения. Студенты ещё не прошли основополагающие предметы естественно научного цикла дисциплин. Знания первокурсников определяются школьными циклами физико-математической подготовки. В разных школах она может существенно отличаться и зависит от принятого направления подготовки учащихся. Поэтому примеры и задачи для практических занятий опирались на системообразующие модели объектов наблюдений, известные и доступные для освоения через Интернет. В качестве конструктивной модели порождения использованы свойства доски Гамильтона и метод имитационного моделирования для выхода на целый комплекс понятий и моделей дискретного анализа.
В приложении А приведены фрагменты геометрического и программного моделирования, связанные с конкретизацией понятий рациональных и эмпирических комплексов систем.
7. Вопросы для самоконтроля
1. История возникновения ОТС. Состав предметов ТС по Берталанфи. Система как понятие. Общая система. Парадигма.
2. Дуальность в определении и классификации систем. Вложенная структура для систем "объект-субъект".
3. Объект. Признаки-свойства, признаки-базы наблюдений. Средства языка описания.
4. Лингвистический уровень описания системы: термы, конституэнты, функторы, правильное высказывание, теория.
5. Теоретико-множественный уровень; кортеж, последовательности, вектора, проекции, декартовый базис для группового описания, термы и функторы...
6. Абстрактно-алгебраический уровень. Алгебраическая операция, алгебраическая структура. Соответствия. Отображения. Отношения.
7. Логико-математический уровень. Логическая операция. Мn —> М. Функции. Базис логического порядка.
8. Топологический уровень. Метрика. Расстояние. Системы координат как база (Р) объекта (S).
9. Изомофизмы объектов и общее свойство. Объекты: треугольник Паскаля, доска Гамильтона, бином Ньютона и его коэффициенты, число логических функций.
10. Динамический уровень. Система обозначений, интерпретация.
11. Эвристический уровень. Интуиция, эвристика, логика. Методология (от Эвклида до наших дней).
12. Метод числового перебора и логическая интерпретация на примере ФАЛ 2-х переменных.
13. Логические, эвристические и интуитивные операции, пример.
14. Автомат как динамическая система..
15. История эвристических методов: Сократ, Архимед, Папп, Галилей, Бэкон; Луллий, Декарт, Лейбниц.
16. Аксиоматический метод и математическая структура. Открытие. Системы аксиом.
17. Групповая операция и род структур.
18. Логические основы формальных систем: от методологии Пифагора до Гильберта и Гёделя.
19. Понятие о парадоксах логики и антиномиях. Формальная логика. Неопределенные высказывания...
20. ФАЛ как математическая структура.
21. Способы представления сложного события
22. Исходная система (S) и объект эмпирической системы. Каналы наблюдений и обобщений.
23. Системы данных; переменные и параметры. Множество баз. Ортогональность при построении образов.
24. Маски порождения. Пример с функцией вычетов.
25. Эпистемология познавательных уровней эмпирических
систем.
26. Системы с поведением. Выборочные переменные..
27. Нормирование и суммирование в системе данных с по-
мощью масок.
28. Мощность множества состояний. Маска для полностью упорядоченных множеств.
29. Порождающие и порождаемые переменные.
30. Вычислительная модель. Семантическая сеть.
31. Решетка методологических типов. Непрерывное через дискретное. Преимущества и недостатки.
32. Функции выбора: недетерминированный случай. Нечет-
кие меры: карта и граф порядка нечетких мер.
33. Мера возможностей, мера логическая, мера вероятностная. Мощность множества.
34. Нейтральные и направленные системы с поведением. Пример разбиения маски. Глубина маски.
35. Меры нечеткости: аксиоматика. Двухальтернативный
случай выбора. Энтропия выбора (до n=10).
Перечень вопросов конкретизируется по мере прохождения программы дисциплины.
Теоретическую часть билетов, т.е. два первых вопроса, образуют вопросы из перечня п.7
Третий вопрос в экзаменационном билете - это задача. Она выбирается из задач и упражнений, приведенных в пособиях по теории систем.
ЗАКЛЮЧЕНИЕ
Для изучения теории систем требуются знания по основам информатики, основам работы с персональным компьютером и его программным обеспечением. Общая теория систем и основы информатики служат базой для обобщения и межпредметного применения полученных знаний при изучении других дисциплин, в частности, системного анализа и исследование операций, теории принятия решений и моделирование систем, банкам данных и базам знаний.
Общая теория систем является основой методологии создания рационального и эмпирического описания реальных объектов и систем, построенного на принципе системного подхода (системной парадигмы).
Изучение дисциплины направлено на решение следующих задач:
· Усвоение основных понятий эпистемологии, как теории познания реальности.
· Отождествление объекта наблюдений с системным принципом и подходом к его описанию.
· Формирование модели объекта наблюдений (модели объекта), составленной из элементов архитектуры рациональных и эмпирических комплексов.
Краткое содержание дисциплины можно определить из приводимого ниже перечня основных ключевых понятий: наука о системах, эпистемология, парадигма, системный подход, рациональные системы, эмпирические системы, уровни абстрагирования и конкретизации, структуризация и метаоперации над системой данных, масочные технологии обработки данных, адресные уравнения, системы с поведением...
По данной дисциплине специальности студент осваивает структуру и принципы построения знаково-лингвистического и теоретико-множественного описания объекта наблюдений в виде комплекса, агрегированного из элементов рациональных и эмпирических систем, умеет перейти от теоретико-множественного описания к формализованному логико-алгебраическому, закладываются исходные знания для систем логического моделирования объекта наблюдений.
ЛИТЕРАТУРА
Основная литература:
1. Панченко В.М.Теория систем: Методологические основы Учебное пособие. - М.: МИРЭА, 2005. -96 с.
2. Панченко В.М. Теория систем: Задачи и примеры Учебное пособие. - М.: МИРЭА, 2005. -80 с.
3. Волкова В.Н., Денисов А.А. Теории систем и системный анализ: Учебник –Изд.-во Юрайт, 2012.-530 с..(Бакалавр)
Дополнительная литература:
4. Сигорский В.П. Математический аппарат инженера: Киев Техника, 1977.- 766 с
5. Клир Дж. Системология. Автоматизация решения системных задач. -М.: Радио и связь, 1990. - 540 с.
6. Панченко В.М. Системный анализ. Метод имитационного моделирования. - М.: МИРЭА, 2005. - 132 с.
7. Методические указания №0802: Теория принятия решений Составитель: В.М. Панченко –М.: РИО МИРЭА, 2009.-28 с.
8. Скляревский Е.С. Удивительный треугольник великого француза// Hard and Soft. – 2003. -№10.
9. Тепляков А. Моделируя жизнь// Hard and Soft. – 2001. -№7.
10. Кузьмин О.В. Треугольник и пирамида Паскаля: свойства и обобщения// Соросовский Образовательный Журнал. -2000. –№5. – с. 101-109.
ПРИЛОЖЕНИЕ А. ИМИТАТОРЫ ПРОЦЕССОВ
В рамках дисциплины «Общая теория систем» в приложении рассматриваются примеры имитационного моделирования в рамках задачи «Рейтинг» обучаемого, а также взаимосвязи доски Гамильтона и треугольника Паскаля, как комплексов рационально-эмпирических систем.
Задача «Рейтинг»
Концептуальная модель задачи «Рейтинг» обучаемого
Для конструктивной постановки задачи “Рейтинг” на эвристическом уровне принимаются следующие гипотезы:
–Общая гипотеза: статистические, априорные и апостериорные данные (прошлые успехи, отношение к учебному процессу и т.д.) косвенно характеризуют эффективность познавательного процесса обучения индивидуума.
– Частная гипотеза: априорная оценка обучаемого F0 может быть выражена функцией двух переменных:
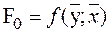, (1.1)
где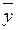 
– средняя оценка обучаемого по априорным данным (данным прошлого опыта);
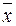– средняя оценка деятельности обучаемого за текущий период познавательного процесса: учебный час, занятие, месяц, семестр, учебный год [2].
Оценка 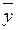может быть определена по данным аттестата зрелости, а в дальнейшем на начальном этапе по зачётной книжке обучаемого.
Оценка 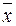– зависит от посещаемости занятий и активности обучаемого во время этих занятий.
Для определения априорной базовой оценки и рейтинга обучаемого в рассматриваемой конкретной задаче “Рейтинг” принята следующая зависимость для F0 (2.1):
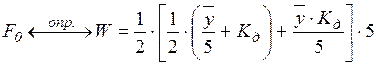(1.2)
где 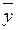– средняя оценка по аттестату зрелости и оценкам Единого государственного экзамена (ЕГЭ) в баллах;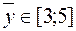 
– коэффициент доверия; оценка деятельности индивидуума в текущем семестре обучения; 
;
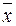– оценка посещаемости в среднем за период наблюдений в относительных единицах; 
;
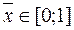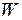– априорная оценка обучаемого в баллах. 
.
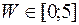Конституэнты формулы (1.2) отражают процесс нормирования и масштабирования информации, связанный с эвристикой следующих исходных предпосылок для шкал оценок:
; 
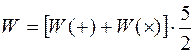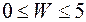; (1.3)
; 
; (1.4)
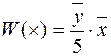; ; (1.5)
Здесь имеем:
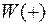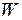– аддитивная составляющая оценки ;
– мультипликативная составляющая оценки .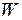
Уяснив семантику, принятую для конституэнт формулы (1.2), можно перейти к её формальному анализу:
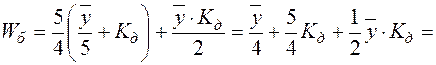
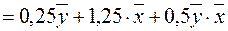. (1.6)
Выражение (1.6) определяется, как концептуальная модель средневзвешанного базового рейтинга обучаемого, вычисляемого по априорным данным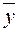 
и результатам наблюдений 
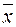(апостериорные данные наблюдений) [2].
|
|
|
