 |
Имитационное моделирование в задаче «рейтинг»
|
|
|
|
Цель эксперимента – изучить и понять динамику изменения средней базовой оценки в зависимости от субъективных вероятностей посещения занятий, задаваемых обучаемым из интуитивных предпосылок в начале семестра, т.е. до сбора реальных данных по 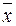 (р).
(р).
Обозначимполученное из субъективных вероятностей значение 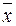 через
через 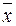 (м) (модели) в отличие от
(м) (модели) в отличие от 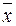 (р) для реальных наблюдений.
(р) для реальных наблюдений.
Формирование исходных данных для задания субъективных вероятностей связано с расписанием практических занятий конкретной группы студентов и поточных лекционных занятий.
В табл. 1.2 приведён запланированный график изучения дисциплины по расписанию занятий.
Эти данные являются составляющими исходной системы объекта (наряду с данными по успеваемости), и служат для построения различных порождающих систем с поведением [4, с. 97–187].
Для моделирования потребуется граф состояний и переходов для стационарного (установившегося) процесса (обучаемый строит граф, исходя из собственного расписания).
На рис. 1.1 представлен граф пространства состояний и переходов для семинаров и лекций при почасовом контроле времени (45 мин. – учебный час). На рис. 1.1 S (н) – начальное состояние; S (к) – конечное состояний; S (1) – первый час занятий (45 мин); S (2) – второй час занятий (45 мин); с – семинар; л – лекция; n – номер недели.
Из начального состояния S (н) обучаемый имеет возможность перейти на первый час занятий S (1), затем или сразу на второй час занятий S (2). В силу случайных факторов он может уйти после любого часа в конечное состояние S (к) или, пропустив час, другой вернуться к концу четырёхчасовой лекции (две пары по 45 мин.).
Обучаемый, исходя из своего прошлого опыта, конструирует свои подграфы, задаваясь вероятностями перехода между вершинами графа P (ij). Множество { P (ij)(S (i)® S (j)} определит систему механизмов случайного выбора, которая позволит имитировать процесс посещения занятий согласно заданного расписания (см. табл. 1.2).
|
|
|
Таблица 1.2. Расписание занятий по дисциплине
| № недели | Дата занятия | час | Вид занятия |
| 13.02.2011 | 1с | ||
| 20.02.2011 | 1л | ||
| 27.02.2011 | 2с | ||
| 06.03.2011 | 2л | ||
| 13.03.2011 | 3с | ||
| 20.03.2011 | 3л | ||
| 27.03.2011 | 4с | ||
| 03.04.2011 | 4л | ||
| 10.04.2011 | 5с | ||
| 17.04.2011 | 5л | ||
| 24.04.2011 | 6с | ||
| 08.05.2011 | 7с | ||
| 15.05.2011 | 6л | ||
| 22.05.2011 | 8с | ||
| 29.05.2011 | 7л |
Для примера в табл. 1.3 приведены соответствующие данные и задан механизм случайного выбора {МСВ} в интервалах случайных чисел (от 0 до 99), определяющих те или иные переходы: S (i) ® S (j).
Циклический граф пространства состояний и переходов при заданных субъективных вероятностях представляет одну из возможных стратегий моделирования процесса посещения занятий, связанную с чётким графиком посещения занятий (см. табл. 1.2).
На рис.1.1 и в табл. 1.3 и 1.4 приведена система для организации процесса имитации к задаче «расписание». Система определяет алгоритм организации имитационного процесса и структуру применяемых механизмов случайного выбора (МСВ) для семинаров и лекций.








Рис.1.1 Пример графа алгоритма деятельности при имитации посещения семинаров и лекций, (см. расписание в табл. 1.5, особенность-занятия начинаются со второй недели)
Таблица 1.3. Матрица S (i) – > S (j) для семинаров и механизм случайного выбора.
| S (i) | S (j) | P (ij) | [ч.н.; ч.к.] {МСВ} |
| Sнс | S1c | 0.90 | 00;89 |
| S2c | 0.05 | 90;94 | |
| Sкс | 0.05 | 95;99 | |
| S1c | S2с | 0.95 | 00;94 |
| Sкс | 0.05 | 95;99 |
Запуск имитационного процесса осуществляется путём задания правил формирования случайных чисел:
· от генератора случайных чисел,
· выборкой из таблицы случайных чисел.
|
|
|
Таблица 1.4. Матрица S (i) – > S (j) для лекций и механизм
случайного выбора.
| S (i) | S (j) | P (ij) | [ч.н.; ч.к.] {МСВ} |
| Sнл | S1л | 0.80 | 00;79 |
| S2л | 0.10 | 80;89 | |
| Sкн | 0.10 | 90;99 | |
| S1л | S2л | 0.90 | 00;89 |
| Sкл | 0.10 | 90;99 |
Для учебных целей рассмотрим имитацию с большой выборкой случайных чисел..
В табл. 1.2 приведены данные имитационного процесса для выборки мощностью в 100 случайных чисел, взятых из таблицы случайных чисел [8, c.122] по столбцам, начиная с адреса K1.
В столбце 1 табл. 1.5 указан номер учебного часа (m (j)). В столбце 2 приведено календарное расписание часов занятий в соответствии с табл. 3.1. Номер и вид занятий приведён в столбце 3. Затем идёт выборка случайных чисел с привязкой к m (j). Если число по результатам имитации не используется, перед ним проставлен знак (–).
Далее в столбцах приведены порождаемые имитацией данные:
S (i) ® S (j) – исходное и получаемое состояния системы (столбцы 5 и 6);
xj – текущий результат имитации;
∑ x – количество посещений на момент m (j);
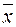 (m(j)) – среднее значение оценки коэффициента доверия по посещаемости, полученное на модели.
(m(j)) – среднее значение оценки коэффициента доверия по посещаемости, полученное на модели.
Таблица 1.5. Данные имитации процесса посещения занятий (фрагмент)
| m (j) | Дата | Занятие | {r(j)} | S(i) | S(j) | x j | ∑ x | 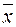 (m) (m)
|
| 13.02 | 1с | Sнс | S1c | |||||
| 13.02 | 1с | S1c | S2c | |||||
| 20.02 | 1л | Sнл | S1л | |||||
| 20.02 | 1л | S1л | S2л | |||||
| 27.02 | 2с | Sнс | Sкc | 0,8 | ||||
| 27.02 | 2с | - | 0,66 | |||||
| 6.03 | 2л | Sнл | S1л | 0,71 | ||||
| 6.03 | 2л | S1л | S2л | 0,75 | ||||
| 13.03 | 3с | Sнс | S1c | 0,78 | ||||
| 13.03 | 3с | S1c | S2c | 0,8 | ||||
| … |
В результате имитационного моделирования процесса посещения занятий получена функциональная зависимость между 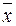 ( m (j)) и m (j). Можно показать, что при переходе от шага j к (j +1) изменение значения шага дискретизации
( m (j)) и m (j). Можно показать, что при переходе от шага j к (j +1) изменение значения шага дискретизации 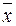 ( m (j)) равно
( m (j)) равно  (j +1)-1. Переход осуществляется от точки
(j +1)-1. Переход осуществляется от точки 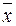 ( m (j)) из множества {
( m (j)) из множества { 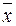 ( m (j))} с мощностью j к ближайшей точке на множестве {
( m (j))} с мощностью j к ближайшей точке на множестве { 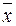 ( m (j +1))} с мощностью (j +1) в направлении, указанном значением xj Î {0,1}. При m (j)® ¥ изменение
( m (j +1))} с мощностью (j +1) в направлении, указанном значением xj Î {0,1}. При m (j)® ¥ изменение 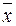 ( m (j)), т.е. D
( m (j)), т.е. D 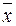 ( m (j +1))®0.
( m (j +1))®0.
Следовательно, переменная 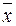 ( m (j)) стремится к постоянной величине и претендует на роль параметра оценки деятельности обучаемого.
( m (j)) стремится к постоянной величине и претендует на роль параметра оценки деятельности обучаемого.
|
|
|
В табл. 1.6 результаты имитационного исследования динамики базовой оценки обучаемого в зависимости от 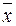 ( mj) при значении
( mj) при значении 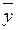 (21)=4,05. Значения базовой оценки определяется по формуле 1.6.
(21)=4,05. Значения базовой оценки определяется по формуле 1.6.
Таблица 1.6. Результаты Имитационного исследования динамики базовой оценки (фрагмент)
| m (j) | 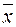 (m) (m)
| 
|
| 4,29 | ||
| 4,29 | ||
| 4,29 | ||
| 4,29 | ||
| 0,8 | 3,63 | |
| 0,66 | 3,17 | |
| 0,71 | 3,34 | |
| 0,75 | 3,47 | |
| 0,78 | 3,57 | |
| 0,8 | 3,63 | |
| … | … | … |
В процессе выполнения данной задачи используются как данные, полученные эмпирическим путем (оценки обучаемого), так и данные по имитации посещения, полученные рациональным методом на основе применения механизма выбора случайных чисел. Таким образом, в процессе моделирования изучается взаимодействие рациональной и эмпирической компонент, что позволяет даже при отсутствии реальных исходных данных уже в начале семестра исследовать влияние ИМИТАТОРА посещаемости занятий на базовую оценку..
В процессе появлении реальных данных о посещении, задача «Рейтинг» решается по аналогии и пошагово по мере накопления этих данных, что важно и для воспитательных целей. Очевидно, что реальный процесс посещения занятий может значительно отличаться от полученного путём имитационного моделирования.
Обучаемый становится участником эксперимента, в ходе которого он должен вести постоянно сбор и обработку реальных данных за каждый день реализации расписания занятий. При этом формируется количественная базовая оценка, косвенно свидетельствующая о прилежании обучаемого. Анализ полученных результатов по ряду обучаемых представляет интересную самостоятельную задачу для исследования.
Данные наблюдений по группе обучаемых показывают, что основной разброс разности оценок W (m) – 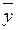 (n) = D W Î[–0,5
(n) = D W Î[–0,5  +0,5] принадлежит ограниченному интервалу значений (
+0,5] принадлежит ограниченному интервалу значений ( 0,5 балла).
0,5 балла).
Интерпретировать точки этого интервала можно по-разному. И как степень усвоения и понимания предмета в целом. И как отношение обучаемого к данному предмету. Могут быть и более интересные интерпретации. Во всяком случае, есть повод для дополнительных исследований и с позиций системного подхода и с позиций системного анализа [2].
|
|
|
Предложенный вычислительный процесс может быть реализован средствами программирования электронных таблиц в пакетах программ оболочки Microsoft Excel.
|
|
|


