 |
Оформление отчета по работе
|
|
|
|
Отчет должен содержать:
1. Номер лабораторной работы.
2. Название лабораторной работы.
3. Цель лабораторной работы.
4. Описание пунктов выполнения лабораторной работы в соответствии с заданием.
5. Вывод по работе.
7.5. Контрольные вопросы
1. Что такое система счисления?
2. Какие системы являются стандартными в информатике?
3. Какие математические функции в OpenOffice.org.Calc можно использовать для перевода чисел из одной системы счисления в другую?
4. Какие специальные функции (функции перевода) в OpenOffice.org.Calc используются для перевода чисел из одной системы счисления в другую?
5. Как переводятся целые и дробные части чисел?
6. Какие цифры входят в запись числа в восьмеричной, шестнадцатеричной системах счисления?
7. Какие цифры входят в запись числа в троичной, пятеричной системах счисления?
8. Какие алгоритмы применяются для перевода десятичного числа в систему счисления с произвольным основанием?
9. Какие алгоритмы применяются для перевода числа, записанного в произвольной системе счисления, в десятичную систему счисления?
10. Что требуется для организации системы счисления с произвольным основанием?
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Тульский государственный университет»
Кафедра
Информационная безопасность
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ЛАБОРАТОРНОЙ РАБОТЕ № 8
по дисциплине
ИНФОРМАТИКА
Разработчик: к.т.н., доц. Баранова Е.М.
Тула, 2018 г.
Лабораторная работа № 8
Специальные возможности электронных таблиц (OOo Calc).
Алгебра логики
Цель лабораторной работы
|
|
|
Получение навыков работы с логическими операциями над двоичными числами при помощи инструментов электронных таблиц (OpenOffice.org.Calc).
Теоретические положения
Основными логическими операциями (связками) являются:
1. Отрицание (НЕ, инверсия). Отрицанием высказывания называется высказывание, ложное, когда заданное высказывание истинно и истинное, когда заданное высказывание ложно.
Отрицание обозначается одним из следующих способов: 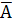 ,
,  , где А – элементарное высказывание.
, где А – элементарное высказывание.
2. Конъюнкция (И, логическое произведение). Конъюнкцией двух элементарных высказываний называется составное высказывание, истинное, когда оба высказывания истины и ложно во всех остальных случаях.
Конъюнкция обозначается одним из следующих способов: А  B, А
B, А  B, А
B, А  B, AB, где А, B – элементарные высказывания.
B, AB, где А, B – элементарные высказывания.
3. Дизъюнкция (ИЛИ, логическое сложение). Дизъюнкцией двух элементарных высказываний называется составное высказывание, ложное, когда оба высказывания ложны и истинное во всех остальных случаях.
Дизъюнкция обозначается одним из следующих способов: А  B, А
B, А 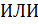 B, А
B, А 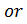 B, A+B, где А, B – элементарные высказывания.
B, A+B, где А, B – элементарные высказывания.
4. Импликация (ЕСЛИ…ТО, логическое следование). Импликацией двух элементарных высказываний называется составное высказывание, ложное, когда первое элементарное высказывание истинно, и истинное во всех остальных случаях.
Импликация обозначается одним из следующих способов: А  B, А
B, А  B, где А, B – элементарные высказывания.
B, где А, B – элементарные высказывания.
5. Эквивалентность (равнозначность). Эквивалентностью двух элементарных высказываний называется составное высказывание, истинное, когда значения элементарных высказываний совпадают и ложное во всех остальных случаях.
Эквивалентность обозначается одним из следующих способов: А 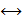 B, А
B, А  B, А
B, А  B где А, B – элементарные высказывания.
B где А, B – элементарные высказывания.
6. Неравнозначность (исключающее ИЛИ, сложение по модулю 2). Неравнозначностью двух элементарных высказываний называется высказывание, когда истинные значения элементарных высказываний не совпадают и ложное во всех остальных случаях.
|
|
|
Неравнозначность обозначается одним из следующих способов: А  B, А
B, А  B, где А, B – элементарные высказывания.
B, где А, B – элементарные высказывания.
7. Стрелка Пирса. Стрелка Пирса – это операция, результат которой равен единице, если оба элементарных высказывания ложны, и равен нулю во всех иных случаях.
Стрелка Пирса обозначается так: А  B.
B.
8. Штрих Шеффера. Штрих Шеффера – это операция, результат которой равен нулю, если оба элементарных высказывания истины, и равен единице во всех иных случаях.
Штрих Шеффера обозначается так: АǀB.
Логическая операция отрицание является унарной, так как логическая связка применима только для одного элементарного высказывания. Логические операции конъюнкция, дизъюнкция, импликация, эквивалентность, неравнозначность являются бинарными, так как соответствующие логические связки соединяют два простых высказывания в одно сложное.
В таблице 1 представлены результаты основных логических операций.
Таблица 1 – Результат основных логических операций
| Аргументы | Инверсия | Конъюнкция | Дизъюнкция | Импликация | Равнозначность | Неравнозначность | Стрелка Пирса | Штрих Шеффера |
| х1 х2 | 
| 
| 
| 
| ~ | 
| 
| | |
| 0 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
Высказывания, выраженные посредством буквенного обозначения элементарных высказываний, логических связок и скобок, называются логическими формулами.
Предпочтительными считаются логические формулы, содержащие меньшее количество отрицаний.
Основными объектами, изучаемыми в алгебре логики, являются логические формулы, состоящие из букв, знаков логических операций и скобок. Примером логической формулы может служить запись вида  .
.
Буквы (или символы) обозначают логические переменные, которые в алгебре логики могут принимать только два значения: ложь или истина.
Знаки логических операций обозначают действия, которые необходимо проделать над переменными.
Скобки, как и в любой формуле, необходимы для установления порядка проведения операций, в данном случае, логических.
Установлен следующий порядок выполнения логических операций (приоритеты логических операций):
|
|
|
- наивысший приоритет, т.е. выполнение операции в первую очередь – отрицание над одним аргументом;
- второй приоритет – конъюнкция;
- третий приоритет – дизъюнкция, равнозначность, неравнозначность, штрих Шеффера, стрелка Пирса;
- четвертый приоритет, т.е. выполнение операции в самую последнюю очередь – импликация.
Приоритеты устанавливаются в зависимости от скобок и следования операций слева направо в логической формуле.
Каждая формула задает логическую функцию, которая, как и входящие в формулу логические переменные, может принимать только два значения: ложь или истина. Таким образом, запись вида  можно назвать логической функцией (логической функцией трех переменных).
можно назвать логической функцией (логической функцией трех переменных).
Преобразования над логическими формулами осуществляются при помощи алгебры логики.
Алгебра логики – алгебра, образованная множеством А={0,1} вместе со всеми возможными на нем логическими операциями.
Каждая логическая операция имеет свое значение для каждого набора переменных (или элементов множества А={0,1}): 00, 01, 10, 11.
В электронных таблицах предусмотрен набор функций, которые выполняют логические операции и называются логическими функциями.
В OpenOffice.org.Calc (OOo Calc) логические функции вызываются так: меню Вставка, команда Функция. Далее в появившемся окне Мастер функций необходимо выбрать категорию Логический.
После этого будут доступны такие функции как:
- AND (конъюнкция);
- FALS (функция, которая возвращает значение «ложь»);
- IF (логическая функция «если»);
- NOT (инверсия);
- OR (дизъюнкция);
- TRUE (функция, которая возвращает значение «истина»);
- XOR (исключающее ИЛИ).
На рисунке 1 показано окно Мастер функций электронной таблицы Calc, где представлен перечень логических функций.

Рисунок 1 – Окно Мастер функций электронной таблицы Calc и перечень логических функций
Имеющийся в Calc набор функций можно использовать для вычисления значений логических операций в логических формулах.
Далее показан пример применения логических функций электронной таблицы Calc для вычисления логических операций.
|
|
|
1. Применение функции AND
Функция AND позволяет получить результат конъюнкции (логического умножения) аргументов.
Функция AND имеет синтаксис: AND (Значение 1, Значение 2…Значение 30). Под значениями понимаются аргументы. Возможен ввод не более 30 значений (аргументов).
Задание 1.
Определить результат логического умножения, если аргумент 1 – 0, аргумент 2 – истина.
Решение задания 1.
Вводятся значения аргументов, вызывается Мастер функций и нажимается кнопка Далее. В ячейки Логическое значение 1 и Логическое значение 2 вводятся значения заданных аргументов (в данном случае, их два). Затем следует нажать кнопку ОК.
Следует отметить, что результат выведен в окне Мастер функций.
На рисунке 2 показано решение задания 1 при помощи логической функции AND.
После нажатия на кнопку ОК результат логического умножения, вычисленный при помощи функции AND возвращается в ячейку электронной таблицы. На рисунке 3 показан результат решение задания 1.

Рисунок 2 – Решение задания 1 при помощи логической функции AND
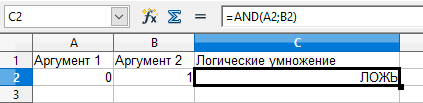
Рисунок 3 – Результат решение задания 1
Таким образом, ответ – ЛОЖЬ или 0.
Задание 2.
Выполнить операцию логического умножения на всех наборах аргументов. Сравнить результаты с таблицей 1.
Решение задания 2.
Создается таблица, со всеми возможными значениями аргументов (все переборы нулей и единиц). Затем вызывается в одну из ячеек логическая функция AND (как при решении задания 1).
Далее необходимо применить формулу ко всем ячейкам, в которых должен содержаться результат, потянув за правый нижний угол ячейки, в которой содержится результат (рисунок 4).
На рисунке 5 показан результат решения задания 2.

Рисунок 4 – Исходные аргументы и применение формулы к ячейкам

Рисунок 5 – Результат решения задания 2
Как видно, результат решения полностью совпадает с таблицей 1 (там, где представлен результат выполнения операции конъюнкции).
Примечание: применение кнопки Выравнивание по центру и полужирного выделения для подписей столбцов таблицы позволит улучшить считывание результата.
2. Применение функции FALS и TRUE
Функция FALS не содержит аргументов, эта функция позволяет возвратить в ячейку электронной таблицы значение ЛОЖЬ.
Функция TRUE не содержит аргументов, эта функция позволяет возвратить в ячейку электронной таблицы значение ИСТИНА.
Задание 3.
Установить для ячейки А8 значение ЛОЖЬ.
Решение задания 3.
Необходимо вызвать окно Мастер функция, выбрать логические функции, а затем функцию FALS. После нажатия на кнопку ОК указанная ячейка А8 будет содержать значение ЛОЖЬ.
|
|
|
Задание 4.
Установить для ячейки В8 значение ИСТИНА.
Решение задания 4.
Необходимо вызвать окно Мастер функция, выбрать логические функции, а затем функцию TRUE. После нажатия на кнопку ОК указанная ячейка В8 будет содержать значение ИСТИНА.
3. Применение функции IF
Функция IF позволяет провести сравнение значений двух аргументов по принципу больше, меньше, равно.
Функция IF имеет синтаксис: IF (Тест; Тогда значение; Иначе значение). Функцию IF можно применить для вычисления значения логической операции импликации (логическое следование).
Примечание: Функция IF может быть использована для вычисления значений иных (любых) логических операций, в частности, равнозначность (эквивалентность).
Задание 5.
Вычислить значение логической функции: Х→Y на всех наборах значений аргументов.
Решение задания 5.
В ячейки электронной таблицы необходимо ввести исходные значения аргументов – нули и единицы (все возможные переборы значений аргументов). Затем вызывается окно Мастер функций, логическая функция IF.
Для применения функции IF в качестве импликации, необходимо знать значения этой операции (в соответствии с таблицей 1). Импликация принимает значение 0, только если первый аргумент истинен (равен 1), второй аргумент ложен (равен 0). На всех других наборах значений аргументов импликация принимает истинные значения (равна 1).
Для решения задачи для функции IF, которая в данный момент будет работать как импликация, вводятся параметры:
- Тест – А2>B2;
- Тогда значение – 0;
- Иначе значение – 1.
Ввод исходных данных и решение задания 5 показано на рисунке 6.

Рисунок 6 – Ввод исходных данных и решение задания 5
После нажатия на кнопку ОК в ячейку С2 будет возвращен результат. Далее следует применить формулу ко всему столбцу (к оставшимся ячейкам С3-С5), для чего необходимо растянуть формулу за нижний правый угол.
Результат решения задания 5 показан на рисунке 7.

Рисунок 7 – Результат решения задания 5
Результат решения совпадает с таблицей 1 (со значениями логической функции импликация).
Примечание: здесь и далее к результату решения применяется форматирование – выравнивание по центру, обрамление и установка гарнитуры шрифта Times New Roman.
Примечание: для просмотра параметров ввода формулы необходимо выделить ячейку, для которой требуется просмотр содержимого, а затем выбрать команду главного меню Вставка, Функция. Откроется окно Мастер функций с включенной закладкой Структура (рисунок 8).

Рисунок 8 – Окно Мастер функций с включенной закладкой Структура
(просмотр содержимого ячейки С2)
Ответ:
- при Х=0, Y=0, значение Х→Y=1;
- при Х=0, Y=1, значение Х→Y=1;
- при Х=1, Y=0, значение Х→Y=0;
- при Х=1, Y=1, значение Х→Y=1.
Задание 6.
Вычислить значение логической функции: 0 →1 → 0 → 1 → 1 → 0.
Решение задания 6.
Решение необходимо вести слева направо.
Целесообразно ввести два аргумента 0 и 1 в ячейки А2 и В2 соответственно, причем ячейки А1, В1…G1 будут содержать подписи столбцов электронной таблицы. В ячейку С2 вставляется функция IF, которая будет вычислять значение импликации (рисунок 9).

Рисунок 9 – Фрагмент решения задания 6
Затем в ячейку D2 также вставляется функция IF при следующих параметрах:
- Тест – С2>А2 (так как теперь определяется значение импликации из того, что содержится в ячейке С2 в 0, а 0 содержится в ячейке А2);
- Тогда значение – 0;
- Иначе значение – 1.
Формула, содержащаяся в ячейке D2 показана на рисунке 10.

Рисунок 10 – Формула, содержащаяся в ячейке D2
Аналогично вводятся функции в ячейки Е2, F2, G2.
Для ячейки Е2 характерны параметры:
- Тест – D2>B2 (так как теперь определяется значение импликации из того, что содержится в ячейке D2 в 1, а 1 содержится в ячейке B2);
- Тогда значение – 0;
- Иначе значение – 1.
Для ячейки F2 характерны параметры:
- Тест – E2>B2 (так как теперь определяется значение импликации из того, что содержится в ячейке E2 в 1, а 1 содержится в ячейке B2);
- Тогда значение – 0;
- Иначе значение – 1.
Для ячейки G2 характерны параметры:
- Тест – F2>A2 (так как теперь определяется значение импликации из того, что содержится в ячейке F2 в 0, а 0 содержится в ячейке A2);
- Тогда значение – 0;
- Иначе значение – 1.
Формулы, содержащиеся в ячейках Е2, F2, G2 показаны на рисунке 11а-11в.

Рисунок 11а – Формула, содержащаяся в ячейке Е2

Рисунок 11б – Формула, содержащаяся в ячейке F2

Рисунок 11в – Формула, содержащаяся в ячейке G2
(конечный результат выполнения задания)
Ответ: значение логической функции – 0.
Примечание: в данной задачи результат логической операции в ячейках отображается в виде 0 и 1 (ранее результат отображался в виде ЛОЖЬ, ИСТИНА). Чтобы настроить формат ячейки, необходимо выделить ячейку, выбрать команду главного меню Формат, затем действие Ячейки. В открывшемся окне Формат ячеек необходимо включить закладку числа. При выборе в поле Категория формата числовой, ячейки, в которые вводятся логические формулы, будут содержать 0 и 1, при выборе формата Логический, ячейки будут содержать значения ЛОЖЬ, ИСТИНА.
4. Применение функции NOT
Функции NOT дополняет (инвертирует) логическое значение.
Функции NOT имеет следующий синтаксис: NOT (Логическое значение).
Задание 7.
Вычислить значение логической функции:  , при X=1, Y=0.
, при X=1, Y=0.
Решение задания 7.
В ячейки А2, В2 электронной таблицы вводятся исходные данные – 1 и 0 соответственно, причем, ячейки А1, В1, а также С2, D2 содержат подписи ячеек.
Ячейка С2 содержит формулу =NOT(A2), которая вставлена через окно Мастер функций как логическая функция NOT (параметр функции или Логическое значение А2).
Ячейка D2 содержит формулу =NOT(B2), которая вставлена через окно Мастер функций как логическая функция NOT (параметр функции или Логическое значение В2).
Примечание: в ячейки формулы можно вводить вручную, без вызова окна Мастер функций при условии знания синтаксиса функции.
Ячейка Е2 содержит формулу =IF(C2>D2;0;1), которая вставлена через окно Мастер функций как логическая функция IF, вычисляющая значение импликации.
Параметры для функции IF, вставленной в ячейку Е2, а также результат выполнения задания 7, показаны на рисунке 12.
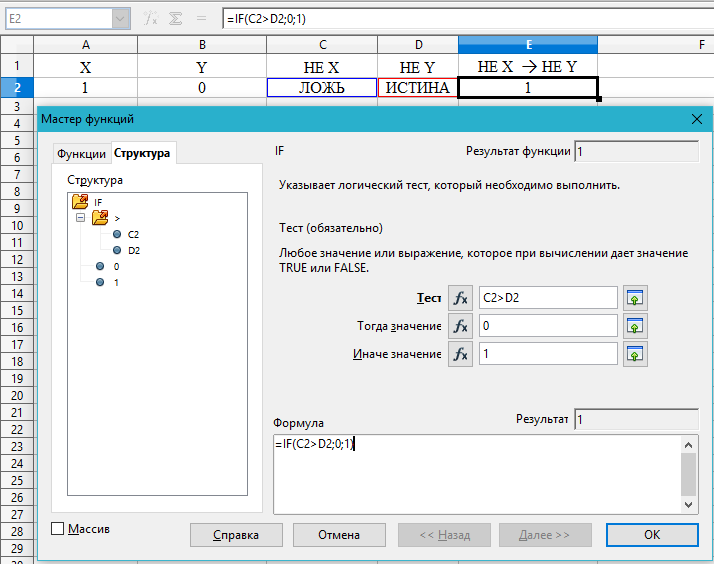
Рисунок 12 – Параметры для функции IF, вставленной в ячейку Е2,
а также результат выполнения задания 7
Ответ: значение функции 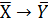 =1.
=1.
Примечание: в электронной таблице знаки отрицаний над аргументами (горизонтальные черточки) заменены на допустимое для инверсии обозначение НЕ.
Задание 8.
Вычислить значение логической функции: 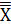 . Сделать выводы.
. Сделать выводы.
Решение задания 8.
Так как не казаны значения аргументов, то операция осуществляется на всех наборах аргумента Х (отрицание или инверсия – это унарная операция, так как она работает на одном аргументе).
Вводятся исходные данные, вызывается функция NOT и указываются ее аргументы. Причем достаточно вызвать функцию NOT один раз, а затем применить формулу к иным ячейкам.
На рисунке 13 показан результат выполнения задания 8 (показана ячейка, к которой изначально была применена функция NOT, и направления применения вставленной формулы).

Рисунок 13 – Результат выполнения задания 8
Ответ:
- при X=0 значение функции 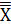 =0;
=0;
- при X=1 значение функции 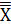 =1.
=1.
Вывод: двойное отрицание приводит к получению исходного значения аргумента, что и выражает закон двойного отрицания.
5. Применение функции OR
Функция OR позволяет получить результат дизъюнкции (логического сложения) аргументов.
Функция OR имеет следующий синтаксис: OR (Значение 1, Значение 2…Значение 30). Под значениями понимаются аргументы. Возможен ввод не более 30 значений (аргументов).
Задание 9.
Вычислить значение логической функции: 0 OR 1 OR 0 OR 0 OR 1 OR 1 OR 0.
Решение задания 9.
В ячейки электронной таблицы вводятся аргументы – всего 7 аргументов (нулей и единиц в заданной логической функции). Затем вызывается окно Мастер функций, логическая операция OR. В поля для ввода значений (аргументов) вводятся исходные данные. Для добавления аргументов (логических значений) следует использовать полосу прокрутки. Затем нажимается кнопка ОК.
На рисунке 14 показано решение задания 9.

Рисунок 14 – Решение задания 9
На рисунке 15 показан результат решения задания 9.
Примечание: для более наглядного отображения результатов решения заданий, следует применять форматирование фрагментов электронных таблиц. В данном случае применено – выравнивание по центру, полужирный шрифт для выделения надписей и обрамление таблицы.
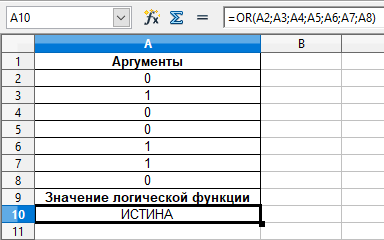
Рисунок 15 – Результат решения задания 9
Ответ: ИСТИНА (или 1).
Задание 10.
Вычислить значение логической функции: Х OR (Y OR Y) OR (Х OR Х).
Решение задания 10.
Если не указаны значения аргументов (Х и Y), то необходимо вести вычисления на всех возможных значениях аргументов (на всех наборах).
Так как в выражении стоят скобки, то следует вести вычисления с учетом скобок.
На рисунке 16 показана расстановка действий или приоритетов выполнения операций с учетом скобок в заданной логической функции:

Рисунок 16 – Расстановка действий или приоритетов
Исходные значения вводятся в ячейки электронной таблицы, причем с учетом расставленных приоритетов:
- первые два столбца аргументы Х, Y (ячейки А2-В5, А1-В1, а также С1-F1 содержат подписи столбцов ячеек электронной таблицы);
- третий столбец – 1 приоритет или Y OR Y (С2-С5);
- четвертый столбец – 2 приоритет или Х OR Х (D2-D5);
- пятый столбец – 3 приоритет или Х OR (Y OR Y), это (E2-E5);
- шестой столбец – 4 приоритет или Х OR (Y OR Y) OR (Х OR Х), т.е. вся функция, это (F2-F5).
Вызывается Мастер функций, логическая операция дизъюнкции, т.е. операция OR.
Вычисления ведутся для каждого столбца. Можно использовать технологию применения формулы к остальным ячейкам (потянуть за нижний правый угол ячейки, содержащей формулу).
Примечание: при вычислении Y OR Y в окне Мастер функций Значение 1 – значение Y, Значение 2 – также значение Y. Аналогично при вычислении Х OR Х: Значение 1 – значение Х, Значение 2 – также значение Х.
На рисунке 17 показано применение логической операции OR (фрагмент решения задания 10).
На рисунке 18 показан результат решения задания 10.
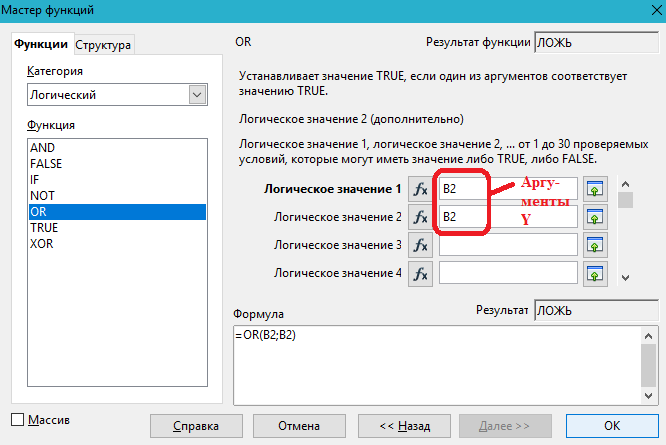
Рисунок 17 – Фрагмент решения задания 10

Рисунок 18 – Результат решения задания 10
Ответ:
- при X=0 Y=0 заданная логическая функция ложна;
- при X=0 Y=1 заданная логическая функция истина;
- при X=1 Y=0 заданная логическая функция истина;
- при X=1 Y=1 заданная логическая функция истина.
6. Применение функции XOR
Функция XOR позволяет получить результат исключающего ИЛИ (сложение по модулю 2) для аргументов.
Функция XOR имеет следующий синтаксис: ХOR (Значение 1, Значение 2…Значение 30). Под значениями понимаются аргументы. Возможен ввод не более 30 значений (аргументов).
Задание 11.
Вычислить значение логической функции: НЕА ХOR (В ХOR НЕВ).
Решение задания 11.
Необходимо расставить приоритеты вычисления операций (рисунок 19).
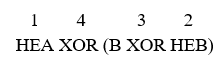
Рисунок 19 – Приоритеты вычисления операций задания 11
Вводятся исходные данные, вычисляются значения операций (для всех наборов значений аргументов).
На рисунке 20 показан результат решения задания 11.

Рисунок 20 – Результат решения задания 11
На рисунке 21 показана структура формулы, содержащейся в ячейке Е2.

Рисунок 21 – Структура формулы, содержащейся в ячейке Е2
Структуры формул, содержащихся в иных ячейках в соответствии с заданием 11, аналогичны.
Примечание: при выполнении операции XOR (для данного задания) в качестве параметров функции используются Логическое значение 1 и Логическое значение 2 (так как операция бинарная, т.е. операция, работающая на парах аргументов, таких как 00, 01, 10, 11).
Ответ:
- при X=0 Y=0 заданная логическая функция ложна;
- при X=0 Y=1 заданная логическая функция ложна;
- при X=1 Y=0 заданная логическая функция истина;
- при X=1 Y=1 заданная логическая функция истина.
Задание 12.
Вычислить значение логической функции: (1<2)  (0>1).
(0>1).
Решение задания 12.
а) Решение задачи можно прописать в любую ячейку электронной таблицы следующим образом: =XOR(1<2;0>1). Результат выполнения задания – ИСТИНА (1), так как введенное выражение можно интерпретировать так: 1 XOR 0 (так как 1<2 – это ИСТИНА или 1, 0>1 это ЛОЖЬ или 0). Результат операции Сложение по модулю 2 для аргументов 1,0 это ИСТИНА (или 1).
б) Решение задания можно выполнить так, как показано на рисунке 22.

Рисунок 22 – Решение задания 12
Структура формулы, содержащейся в ячейке А6, аналогична записи в строке для ввода данных в ячейки электронной таблицы.
Ответ: значение функции (1<2)  (0>1) истинно (равно 1).
(0>1) истинно (равно 1).
7. Вычисление логических операций равнозначность, стрелка Пирса, штрих Шеффера
Электронная таблица OpenOffice.org.Calc (OOo Calc) не содержит специальных функций для работы с такими логическими операциями как равнозначность, стрелка Пирса, штрих Шеффера. Указанные операции можно реализовать при помощи функции IF.
Задание 13.
Вычислить значение логической функции: (1<1) ~ (1>1) ~ (1=1).
Решение задания 13.
а) Решение задания можно оформить в виде проверки трех заданных условий (рисунок 23).

Рисунок 23 – Проверка трех заданных условий задания 13
Примечание:
- для Условия 2 характерна запись формулы в ячейке С2: =IF (A2>A2;1;0);
- для Условия 3 характерна запись формулы в ячейке D2: =IF (A2=A2;1;0);
- для Функции характерна запись формулы в ячейке E2: =IF (B2=C2=D2;1;0).
Действительно, выражение (1<1) ~ (1>1) ~ (1=1) можно записать в виде: ЛОЖЬ ~ ЛОЖЬ ~ ИСТИНА или 0~0~1, что тоже самое. Тогда, в соответствии с таблицей 1 будет получено решение: 0~0=1, 1~1=1.
Ответ: значение функции (1<1) ~ (1>1) ~ (1=1) истинно (равно 1).
б) Решение задания можно оформить в виде проверки одного сложного условия (рисунок 24).
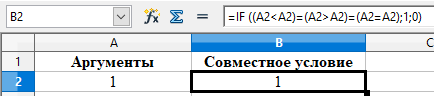
Рисунок 24 – Проверка одного условия задания 13
Ответы совпали.
Задание 14.
Доказать или опровергнуть тождественное равенство: 

 =
= 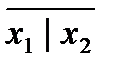
Решение задания 14.
Результат решения задания 14 представлен на рисунке 25.
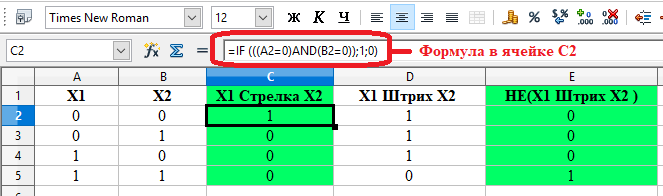
Рисунок 25 – Результат решения задания 14
Формула в ячейке С2 применена ко всему столбцу – ячейки С3-С5.
Для ячейки D2 формула имеет вид: =IF (((A2=1)AND(B2=1));0;1). Формула также применена ко всему столбцу – ячейки D3-D5.
Для ячейки Е2 формула имеет вид: =NOT(D2). Формула также применена ко всему столбцу – ячейки E3-E5.
Ответ: тождественное равенство логического выражения 

 =
= 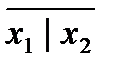 опровергнута, так как значения выделенных цветом столбцов не совпали.
опровергнута, так как значения выделенных цветом столбцов не совпали.
Примечание: логические выражения является тождественно равными, если значения этих выражений равны на всех наборах значений аргументов, входящих в них.
Задание 15.
Вычислить значение логической функции: f(A,D,C)=A|B  C.
C.
Решение задания 15.
Исходное логическое выражение имеет три аргумента. Количество переборов значений аргументов определяется формулой:
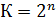 , (1)
, (1)
где К –количество переборов значений аргументов;
n – количество аргументов в логическом выражении;
2 – основание системы счисления (в логических выражениях используются два символа 0,1, следовательно, система счисления – двоичная).
Тогда, количество переборов значений аргументов будет: 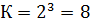 .
.
Это переборы – 000, 001, 010, 011, 100, 101,110, 111.
Примечание, для большинства заданий, решенных выше количество переборов значений аргументов было  (00, 01, 10, 11), так как логические функции содержали два аргумента.
(00, 01, 10, 11), так как логические функции содержали два аргумента.
Результат выполнения задания 15 представлен на рисунке 26.

Рисунок 26 – Результат выполнения задания 15
Формула в ячейке D2 применена ко всему столбцу – ячейки D3- D9.
Формула в ячейке Е2 имеет вид: =IF (((D2=0)AND(C2=0));1;0). Формула, введенная в ячейку Е2, применена ко всему столбцу – ячейки Е3- Е9.
Примечание: формулы, содержащиеся в ячейках, можно копировать и вставлять в другие ячейки электронной таблицы.
Ответ:
- при А=0, В=0, С=0 функция f(A,D,C)=A|B  C ложна (равна 0);
C ложна (равна 0);
- при А=0, В=0, С=1 функция f(A,D,C)=A|B  C ложна (равна 0);
C ложна (равна 0);
- при А=0, В=1, С=0 функция f(A,D,C)=A|B  C ложна (равна 0);
C ложна (равна 0);
- при А=0, В=1, С=1 функция f(A,D,C)=A|B  C ложна (равна 0);
C ложна (равна 0);
- при А=1, В=0, С=0 функция f(A,D,C)=A|B  C ложна (равна 0);
C ложна (равна 0);
- при А=1, В=0, С=1 функция f(A,D,C)=A|B  C ложна (равна 0);
C ложна (равна 0);
- при А=1, В=1, С=0 функция f(A,D,C)=A|B  C истинна (равна 1);
C истинна (равна 1);
- при А=1, В=1, С=1 функция f(A,D,C)=A|B  C ложна (равна 0).
C ложна (равна 0).
Задание на работу
1. Изучите теоретические положения лабораторной работы.
2. Открыть электронную таблицу OpenOffice.org.Calc (OOo Calc).
3. Порешать задания 1-15 из теоретических положений лабораторной работы (каждую функцию можно располагать на отдельном листе электронной книги, при этом результаты решения заданий должны быть отформатированы). Решенные задания 1-15 сохранить в файл Задания_решенные.
4. При помощи логических функций электронной таблицы Calc вычислите значения следующих логических формул:
а)  ;
;
б)  ~
~ 
в) 
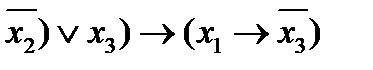 .
.
5. При помощи логических функций электронной таблицы Calc доказать или опровергнуть равносильность логических выражений:
б)  |
|  =
=  ;
;
в) 

 =
=  .
.
6. При помощи логических функций электронной таблицы Calc определить логически истинные выражения из ниже представленных:
а) А ИЛИ НЕ А И НЕ А;
б) НЕ А И НЕ В И НЕ А;
в) А ИЛИ НЕА И НЕ В;
г) НЕ А И В ИЛИ А;
д) НЕ А ИЛИ А ИЛИ А;
е) А ИЛИ С И В;
ж) А ИЛИ НЕ С И НЕ В;
з) А И НЕ С ИЛИ В;
и) ЕСЛИ (А И НЕ В), ТО А ИЛИ В;
к) ЕСЛИ (А И НЕ В), ТО (С ИЛИ В И А).
7. При помощи логических функций электронной таблицы Calc составить таблицы истинности следующих функций:
а)  ;
;
б) 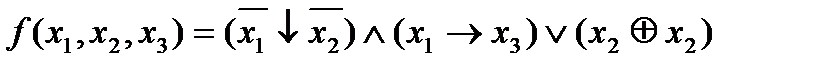 ;
;
в)  ;
;
г)  .
.
8. Результаты решения заданий пунктов 4-8 Задания на работу сохранить в файл Задания_самостоятельные.
9. Ответить на контрольные вопросы.
10. Показать результаты работы преподавателю.
11. Оформить отчет.
|
|
|


