Электрические цепи с одним источником энергии и пассивными (резистивными) элементами

Многие электрические цепи имеют лишь один источник энергии и то или иное число пассивных (резистивных) элементов. Это могут быть приемники электрической энергии и различные вспомогательные элементы.

Расчет и анализ неразветвленных и некоторых разветвленных цепей с одним источником и пассивными элементами производится с помощью закона Ома, первого и второго законов Кирхгофа, не требует совместного решения уравнений. Во многих случаях расчет и анализ осуществляются путем замены отдельных участков, а затем всей цепи одним элементом с эквивалентным сопротивлением и последующего перехода в процессе расчета к заданной цепи. В некоторых случаях целесообразно воспользоваться методом эквивалентного генератора

Электрические цепи с последовательным соединением резистивных элементов.

Последовательным называется такое соединение элементов, когда условный конец первого элемента соединяется с условным началом второго, конец второго — с началом третьего и т. д. Характерным для последовательного соединения является один и тот же ток во всех элементах. Последовательное соединение нашло широкое применение на практике. Например, последовательно с приемником r часто включается резистор r_р для регулирования напряжения, тока или мощности приемника (рис. 1.5,а). Для расширения пределов измерения вольтметров последовательно с ними включают добавочные резисторы r_д (рис. 1,5, б). С помощью реостата, включаемого последовательно в различные ветви цепи двигателя постоянного тока, производят изменение его пускового тока или частоты вращения.

 

Рис. 1.5. Схема электрических цепей с последовательным соединением резистивных элементов

 

В общем случае при последовательном соединении и резистивных элементов (рис. 1.5, в) ток в цепи, напряжения на элементах и потребляемые ими мощности определяются следующими соотношениями:

, ,

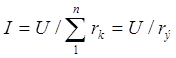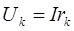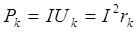
где k = 1, 2,..., n — номер элемента; r_э = Σr_k — эквивалентное сопротивление цепи.

Напряжение и мощность всей цепи

,

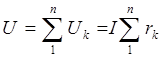Соотношение между напряжениями, мощностями и сопротивлениями элементов

U_k /U_l = P_k /P_l = r_k /r_l,

где l = 1, 2,..., n — номер элемента.

С помощью приведенных формул нетрудно выяснить характер изменения тока, напряжений и мощностей при изменении значений сопротивлений или числа включенных резистивных элементов. Например, если увеличить число элементов, то эквивалентное сопротивление возрастает, а ток, напряжения и мощности ранее включенных элементов уменьшаются; уменьшается также и общая мощность.

Приемники электрической энергии последовательно, как правило, не соединяются, так как при этом требуется согласование номинальных данных приемников, исключается возможность независимого их включения и отключения, а при выходе из строя одного из приемников отключаются также остальные приемники. Чаще их включают параллельно.

Электрические цепи с параллельным соединением резистивных элементов.

Параллельным называется такое соединение резистивных элементов, при котором соединяются между собой как условные начала всех элементов, так и их концы (рис. 1.6, а). Характерным для параллельного соединения является одно и то же напряжение U на выводах всех элементов. Параллельно соединяются обычно различные приемники электрической энергии и другие элементы электрических цепей, рассчитанные на одно и то же напряжение. При параллельном соединении не требуется согласовывать номинальные данные приемников, возможно включение и отключение любых приемников независимо от остальных, а при выходе из строя какого-либо приемника остальные остаются включенными.

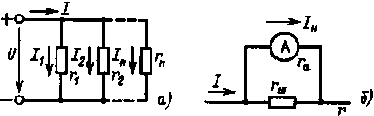
Рис. 1.6. Схемы электрических цепей с параллельным соединением резистивных элементов

Параллельное соединение применяется часто для расширения пределов измерения амперметров (рис. 1.6,б): если ток I в электрической цепи превышает номинальный ток I_ном амперметра, параллельно с ним включают шунтирующий резистор r_ш. Нередко параллельное соединение используют для уменьшения эквивалентного сопротивления какого-либо участка электрической цепи.

Токи и мощности параллельно соединенных ветвей (рис. 1.6, а) при U = const не зависят друг от друга и определяются по формулам

I_k = U/r_k = Ug_k; P_k = UI_k = U²/r_k = U²g_k = I_k²r_k.

Ток и мощность всей цепи

;

,

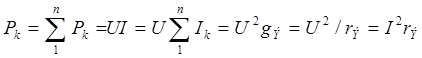где 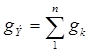— эквивалентная проводимость; r_э=1/g_э — эквивалентное сопротивление.

Соотношения между токами, мощностями, проводимостями и сопротивлениями:

I_k /I_l = P_k /P_l = g_k /g_l = r_l /r_k.

При увеличении числа параллельно соединенных ветвей эквивалентная проводимость электрической цепи возрастает, а эквивалентное сопротивление соответственно уменьшается. Это приводит к увеличению тока I. Если напряжение остается постоянным, то увеличивается также общая мощность Р; токи и мощности ранее включенных ветвей не изменяются.

 

Электрические цепи со смешанным соединением резистивных элементов.

Смешанным, или последовательно-параллельным, называется такое соединение резистивных элементов, при котором на одних участках электрической цепи они соединены параллельно, а на других последовательно.

Смешанное соединение имеет место, например, при питании приемников с сопротивлениями r₁ и r₂ по проводам электрической сети с сопротивлениями r_л (рис. 1.7, а), при регулировании напряжения приемника r с помощью делителя напряжения (потенциометра) r_д (рис. 1.8, а), в случае измерения вольтметром напряжения на одном из резисторов (рис. 1.8, б).

Анализ и расчет электрических цепей со смешанным соединением резистивных элементов производится чаще всего путем предварительных их преобразований. Рассмотрим в качестве примера последовательность расчета электрической цепи, изображенной на рис. 1.7, а.

Пример 1.2. В электрической цепи рис. 1.7,a U = 115 В, r₁= 20 Ом, r₂ = 30 Ом, r_л = 0,5 Ом.

Определить токи, напряжение U_ab приемников, мощности приемников, потери напряжения и мощности в проводах, мощность, потребляемую от источника.

Решение. Электрическая цепь рис. 1.7,а может быть заменена цепями, изображенными на рис. 1.7,б и в, в которых

,

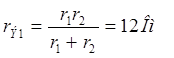Используя электрическую цепь, изображенную на рис. 1.7,в, определим ток I, а перейдя к цепям рис. 1.7, а и б, найдем напряжение U_ab и токи I₁ и I₂:

I = U/r_э ≈ 8,85 A; U_ab = Ir_э1 = 106,2 В;

I₁ = U_ab/r₁ ≈ 5,31 А; I₂ = U_ab /r₂ ≈ 3,54 А

Мощности приемников и мощность, потребляемая из сети,

P₁ = U_ab I₁≈ 564 Вт, Р₂ = U_ab I₂ ≈ 376 Вт,

Р = UI ≈ 1018 Вт.

Рис. 1.7. Схема электрической цепи (а) к примеру 1.2 и схемы эквивалентных ей цепей (б и в)

 

Потери напряжения и мощности в проводах

2I_лr_л = 8,85 В, 2I_л²r_л ≈ 78 Вт.

Используя соотношения, полученные в примере 1.2, нетрудно сделать следующие важные выводы в отношении характера изменения различных величин при смешанном соединении резистивных элементов. С увеличением числа приемников в электрической цепи (см. рис. 1.7, а) сопротивления r_э1 и r_э уменьшатся. Это приведет к увеличению тока I, мощности Р, потерь напряжения 2Ir_л и мощности 2I²r_л. Из-за увеличения потерь напряжения в проводах снизится напряжение U_ab и как следствие этого уменьшатся токи I₁ и I₂, а также мощности P₁ и Р₂.

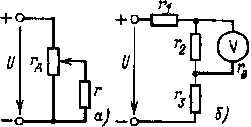
Рис. 1.8 Примеры электрических цепей со смешанным соединением резистивных элементов

 

Чтобы напряжение приемников незначительно колебалось при изменении их числа или режима работы и было близким к номинальному, площадь поперечного сечения S проводов рассчитывают по допустимой потере напряжения ΔU при номинальном режиме из формулы

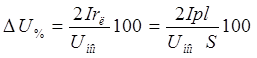
В электрических цепях различного назначения допустимая потеря напряжения лежит примерно в пределах 2 — 6%.

Из двух сечений проводов, определенных по нагреванию и допустимой потере напряжения, выбирают большее.

 

Электрические цепи, содержащие соединения резистивных элементов треугольником.

Под соединением треугольником (рис. 1.9,а) понимается такое, при котором вывод К1 одного из элементов соединяется с выводом Н2 второго, вывод К2 второго - с выводом Н3 третьего, а вывод К3 третьего — с выводом H1 первого элемента. Узловые точки a, b и с подключаются к остальной части электрической цепи.

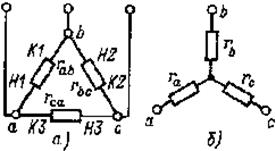
Рис. 1.9. Схема соединения резистивных элементов треугольником (а) и звездой (б)

Для упрощения анализа и расчета некоторых электрических цепей, содержащих соединения резистивных элементов треугольником, целесообразно заменить их эквивалентными резистивными элементами, соединенными звездой (рис. 1.9,б). Примером подобных электрических цепей являются мостовые цепи (рис. 1.10, а). Как видно, в мостовой цепи резистивные элементы образуют два смежных треугольника (rab, rbc, rcaиrbc, rbd, rdc) и нет ни одного элемента, который был бы соединен с другими последовательно или параллельно. Это осложняет расчет и анализ электрической цепи. Однако если заменить, например, резистивные элементы r_ab, r_bc и r_са, соединенные треугольником, эквивалентными элементами r_a, r_b и r_с, соединенными звездой (рис. 1.10,б), то получим цепь со смешанным соединением резистивных элементов, методика расчета которой была рассмотрена выше.

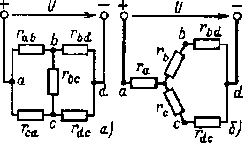
Рис. 1.10. Схема мостовой цепи (а) и соответствующая ей схема после замены одного из треугольников звездой (б)

Замена треугольника резистивных элементов эквивалентной звездой должна производиться таким образом, чтобы после указанной замены токи в остальной части цепи, а также напряжения между точками ab, be и са остались без изменения.

С помощью законов Кирхгофа можно получить следующие формулы для определения сопротивлений эквивалентной звезды:

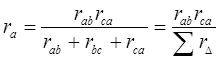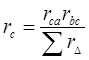; ; (1.23)

Иногда оказывается целесообразным заменить резистивные элементы, соединенные звездой, эквивалентным треугольником. Соответствующие формулы можно получить путем совместного решения выражений (1.23).

Следует заметить, что для расчета мостовых цепей часто используется метод эквивалентного генератора (см. § 1.14 и пример 1.4).

 

ПОНЯТИЕ ОБ ИСТОЧНИКЕ ТОКА

В подавляющем большинстве случаев при расчете и анализе электрических цепей используют источники электрической энергии с параметрами Е и r₀, т. е. источники ЭДС, либо источники с указанными напряжениями. Именно с такими источниками энергии и приходится чаще всего иметь дело на практике. Однако иногда оказывается целесообразным заменить источник ЭДС эквивалентным ему источником тока, параметрами которого являются неизменные по значению ток короткого замыкания I_к и сопротивление r₀. Познакомимся с источником тока на примере электрической цепи рис. 1.4, а, в которой источник ЭДС заменим эквивалентным источником тока.

Источник тока следует считать эквивалентным в том случае, если после замены им источника ЭДС значения тока I, напряжения U и отдаваемой источником мощности UI при различных значениях сопротивления r внешней цепи остаются без изменения. Очевидно, это условие будет выполнено, если источник тока будет иметь такую же внешнюю характеристику, какую имеет источник ЭДС.

Воспользуемся указанным соображением для обоснования структуры электрической цепи источника тока. Разделив левую и правую части уравнения внешней характеристики источника ЭДС (1.15) на сопротивление r₀, получим

U/r₀ = E/r₀ - I, (1.24)

где E/r₀ = I_к - ток короткого замыкания источника ЭДС, являющийся вместе с тем одним из параметров источника тока; U/r₀ = I₀ - некоторый ток, определяемый как частное от деления U на r0. Решив (1.24) относительно Е/r₀, получим E/r₀ = U/r₀ + I, или

I_к = I₀ + I. (1.25)

Так как токи I₀ и I определяются путем деления одного и того же напряжения U на соответствующие сопротивления, то в электрической цепи с источником тока должны быть две ветви с соединенными параллельно резистивными элементами r₀ и r. Согласно (1.25) параллельно указанным ветвям должна быть включена третья ветвь, содержащая элемент с током I_к.

Схема электрической цепи, эквивалентная приведенной на рис. 1 4,а, но содержащая источник тока, дана на рис. 1.11,а. Элемент с током I_к в совокупности с резистором r₀ и представляет собой источник тока.

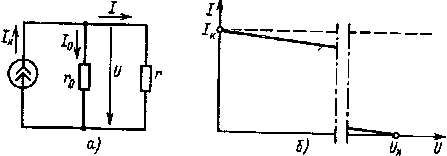
Рис. 1.11. Схема электрической цепи с источником тока (а) и внешняя характеристика источника тока (б)

Записав (1.25) в виде

I = I_к - I₀ = I_к - U/r₀, (1.26)

получим уравнение внешней характеристики I(U) источника тока, которое представляет собой по существу несколько преобразованное уравнение (1.15) источника ЭДС. Уравнение (1.26) и внешняя характеристика, построенная с помощью этого уравнения (рис. 1.11,б), дадут при любом режиме работы цепи такие же значения тока I и напряжения U, как и в случае источника ЭДС. Убедимся в сказанном и рассмотрим попутно последовательность расчета простейшей цепи с источником тока (рис. 1.11, а). Будем считать, что параметры I_к, r₀ и r цепи с источником тока, а также Е эквивалентного источника ЭДС известны.

При холостом ходе r = ∞, 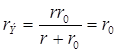, U = I_кr_э = I_кr₀; так как у источника тока I_кr₀ = Е, то и U = Е; I = U/r = E/r = 0.

При коротком замыкании r = 0, , U = I_кr_э = 0, I₀ = U/r₀ = 0, I = I_к; поскольку у источника тока I_к = Е/r₀, то и I = Е/r₀.

Как видно, токи I и напряжения U во внешней цепи источника тока при r = ∞ и r = 0 определяются в конечном итоге по тем же формулам, что и в случае источника ЭДС. Это значит, что токи и напряжения источников тока и напряжения будут равны.

Для замены источника тока эквивалентным источником ЭДС и наоборот достаточно воспользоваться приведенной ранее формулой I_к = Е/r₀.

Источник тока удобно использовать для расчета и анализа, когда r₀ >> r. В этом случае можно считать, что при изменении сопротивления r приемника I₀ ≈ 0 и I ≈ I_к. Напряжение U и мощность Р = UI, потребляемая приемником, будут, конечно, при этом изменяться, так как

U = Ir ≈ I_кr и Р = UI ≈ UI_к = I_к²r. Указанное соотношение сопротивлений (r0 >> r) может быть получено, если под r₀ понимать сумму внутреннего сопротивления источника ЭДС и сопротивления некоторого резистора, включенного в цепь последовательно с источником.

Источник тока считается идеальным, если r₀ = ∞. В цепи с идеальным источником при любых режимах работы I₀ = 0, а I = I_к.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: