 |
Действующее и среднее значения синусоидальных тока, ЭДС и напряжения
|
|
|
|
Для установления эквивалентности переменного тока в отношении энергии и мощности, общности методов расчета, а также сокращения вычислительной работы изменяющиеся непрерывно во времени токи. ЭДС и напряжения заменяют эквивалентными неизменными во времени величинами. Действующим или эквивалентным значением называется такой неизменный во времени ток, при котором выделяется в резистивном элементе с активным сопротивлением r за период то же количество энергии, что и при действительном изменяющемся синусоидально токе.
Энергия за период, выделяющаяся в резистивном элементе при синусоидальном токе,

При неизменном во времени токе энергия
W = I2rT
Приравняв правые части

получим действующее значение тока

Таким образом, действующее значение тока меньше амплитудного в √2 раз.
Аналогично определяют действующие значения ЭДС и напряжения:
Е = Em /  , U = Um /
, U = Um /  .
.
Действующему значению тока пропорциональна сила, действующая на ротор двигателя переменного тока, подвижную часть измерительного прибора и т. д. Когда говорят о значениях напряжения, ЭДС и тока в цепях переменного тока, имеют в виду их действующие значения. Шкалы измерительных приборов переменного тока отградуированы соответственно в действующих значениях тока и напряжения. Например, если прибор показывает 10 А, то это значит, что амплитуда тока
Im =  I = 1,41 • 10 = 14,1 A.
I = 1,41 • 10 = 14,1 A.
и мгновенное значение тока
i = Im sin (ωt + ψ) = 14,1 sin (ωt + ψ).
При анализе и расчет выпрямительных устройств пользуются средними значениями тока, ЭДС и напряжения, под которыми понимают среднее арифметическое значение соответствующей величины за полпериода (среднее значение за период, как известно, равно нулю):
|
|
|
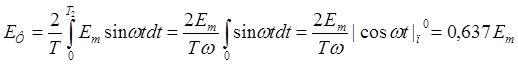
Аналогично можно найти средние значения тока и напряжения:
Iср = 2Iт /π; Uср = 2Uт /π.
Отношение действующего значения к среднему значению какой-либо периодически изменяющейся величины называется коэффициентом формы кривой. Для синусоидального тока

ВЕКТОРНЫЕ ДИАГРАММЫ
Для упрощения анализа и расчета цепей переменного тока целесообразно использовать векторы.
В электротехнике векторами изображаются изменяющиеся синусоидально ЭДС, напряжения и токи, но в отличие от векторов, которыми изображались силы и скорости в механике, эти векторы вращаются с постоянной угловой частотой ω и не означают направление действия.
Допустим, что радиус-вектор ОА (рис. 2.3,а), представляющий собой в определенном масштабе амплитудное значение ЭДС Ет, вращается с постоянной угловой частотой ω = 2 πf против часовой стрелки. Проекция вектора ОА на вертикальную ось (ось у) будет равна
Оа = ОA sin α.
Выразив ОА через амплитудное значение ЭДС Е т и α через ωt, получим выражение мгновенного значения ЭДС, изменяющейся синусоидально:
е = Ет sin ωt.
График мгновенных значений ЭДС изображен на рис. 2.3,б. За начало отсчета выбран момент времени, когда радиус-вектор совпадает с горизонтальной осью (ось х).

Рис. 2.3. Вращающиеся векторы (а) и график мгновенных значений синусоидальной ЭДС (б)
Если в момент t =0 радиус-вектор ОА совпадает с линией, расположенной под углом ψ к оси х, то проекция Оа' и, следовательно, ЭДС будут соответственно равны
Оа' = ОА' sin (ωt + ψ), е = Em sin (ωt + ψ).
Аналогично можно представить в виде векторов, вращающихся против часовой стрелки с постоянной угловой частотой ω, напряжение и ток.
Расчет цепей синусоидального тока производят в действующих значениях ЭДС, напряжений и токов. При этом суммирование Е, U, I проще осуществить с помощью вращающихся векторов, вместо того чтобы, сложив мгновенные значения е, и, i, определить действующие значения результирующих Е, U, I интегрированием гармонических функций. Адекватность этих действий можно обосновать так.
|
|
|
Допустим, что в каком-то узле цепи переменного тока (рис. 2.4, а) известны значения токов i1 и i2:
i1 = I1msin (ωt + ψ1);
i2 = I2msin (ωt + ψ2).
Требуется определить ток i.
На основании первого закона Кирхгофа мгновенное значение тока
i = i1 + i2,
т. e.
i = I1msin (ωt + ψ1) + I2msin (ωt + ψ2).
Ток i можно определить аналитически путем тригонометрических преобразований или графически сложением графиков мгновенных значений токов i1 и i2, как это сделано на рис. 2.4, б. Результирующий ток также изменяется синусоидально и в соответствии с рис. 2.4, б
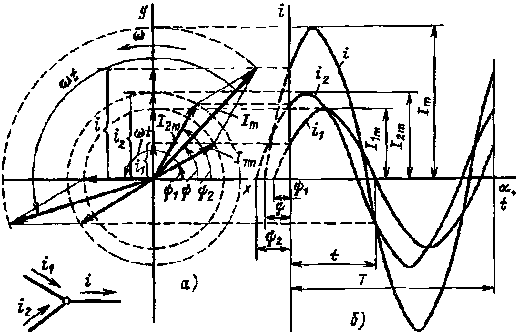
Рис. 2.4. Сложение синусоидальных токов с помощью векторов (а): графики мгновенных значений токов (б)
i = Im sin (ωt + ψ).
Значительно проще произвести сложение токов i1 и i2, если изобразить амплитуды токов в виде векторов и сложить их по правилу параллелограмма. На рис. 2.4, а амплитуды токов I1m и I2m изображены в виде векторов под углами начальных фаз ψ1 и ψ2 относительно оси х. По прошествии времени t векторы повернутся на угол α = ωt. Проекции амплитуд на ось у составят
i1 = I1msin (ωt + ψ1);
i2 = I2msin (ωt + ψ2).
Сложив векторы I1m и I2m по правилу параллелограмма (см. рис. 2,4, а), получим амплитуду результирующего тока Im. Сумма проекций токов I1m и I2m равна проекции результирующего тока Im:
i = i1 + i2.
Полученное выражение соответствует первому закону Кирхгофа для рассматриваемого узла цепи (см. рис. 2.4, а). Из рис. 2.4. а видно, что взаимное расположение векторов I 1m, I 2m и I m в любой момент времени остается неизменным, так как они вращаются с постоянной угловой частотой ω. Аналогично можно определить сумму нескольких изменяющихся синусоидально с одинаковой частотой напряжений или ЭДС Например, в последовательной цепи переменного тока действуют три напряжения:
u1 = U1m sin (ωt + ψ1);
u2 = U2msin (ωt + ψ2);
u3 = U3msin (ωt + ψ3).
Сумму u = u1 + u2 + u3 напряжений можно определить путем сложения векторов их амплитуд (рис. 2.5)

Рис 2.5. Векторная диаграмма напряжений
Ūm = Ū1m + Ū2m + Ū3m
и последующей записи результирующего напряжения u = Um sin (ωt + ψ).
Совокупность нескольких вращающихся векторов, соответствующих уравнениям электрической цепи, называется векторной диаграммой.
|
|
|
Обычно векторные диаграммы строят не для амплитудных, а для действующих значений. Векторы действующих значений отличаются от векторов амплитудных значений только масштабами, так как
I = Im /  .
.
При построении векторных диаграмм обычно один из исходных векторов располагают на плоскости произвольно, остальные же векторы — под соответствующими углами к исходному. При этом в подавляющем большинстве случаев можно обойтись без нанесения осей координат х и у.
|
|
|


