Теория ползучести грунтов.

В теории ползучести в уравнение связи между напряжениями и деформациями входит дополнительно время в явном или неявном виде. Связь между деформацией, напряжением и временем может быть выражена графически, например, в виде кривых ползучести (см. рис. 5.7, а) или изохронных диаграмм деформирования (рис. 5.7, б), а также в формульном виде.

В зависимости от принятой математической формы связи между напряжениями, деформациями и временем согласно классификации академика Ю.Н. Работнова (1966) различают простейшие теории ползучести, метод реологических моделей и наследственные теории ползучести.

 

Рис. 5.7. Виды кривых сдвиговых деформаций грунта при различных постоянных касательных напряжениях (а) и изохронных диаграмм деформирования для различных моментов времени (б): 1 – затухающая ползучесть; 2 – установившаяся ползучесть; 3 - прогрессирующее течение.

В простейших теориях ползучести уравнения состояния, то есть уравнения связи между напряжениями, деформациями и временем, построены исходя из опытов с постоянными нагрузками. Среди них различают теории старения, установившегося течения и упрочнения, описываемые соответственно уравнениями:

, (5.15)

где f - функция; t - время.

Впервые применимость к грунтам простейших теорий ползучести установил С.Р. Месчан (1969). Теория старения нашла широкое применение к грунтам ввиду ее простоты. Теорию установившегося течения целесообразно использовать, если кривые ползучести (см. рис. 5.7, а) имеют значительный участок установившейся ползучести. Теория упрочнения дает хорошие результаты для затухающей ползучести, в частности для компрессионного и объемного уплотнения грунтов. В формулах (5.15) функция f может быть выражена степенной, экспоненциальной, гиперболической, полулогарифмической и другими более сложными зависимостями.

В методе реологических моделей (Максвелл, 1867) уравнения состояния строятся на основании описания поведения механических моделей, конструируемых из соединяемых различными способами простейших элементов (рис. 5.8): пружины (элемент Гука), демпфера (элемент Ньютона) и др.

 

 

Рис. 5.8. Элементы Гука (а); Ньютона (б); реологические модели Максвелла (в); Кельвина-Фойгта (г).

 

Собственные уравнения состояния элементов Гука и Ньютона имеют соответственно вид

, , (5.16)

где Е и η - модуль упругости и коэффициент вязкости материала.

Соединяя упругий и вязкий элемент последовательно и параллельно, получают модели Максвелла и Кельвина-Фойгта (см. рис. 5.8), уравнения состояния которых имеют вид дифференциальных уравнений первого порядка

; (5.17)

. (5.18)

Увеличивая число элементов и соединяя их более сложными способами, получают линейные дифференциальные уравнения с постоянными коэффициентами, порядок которых зависит от числа вязких элементов. Решением указанных уравнений являются экспоненциальные функции или их суммы, что ограничивает применение метода реологических моделей. Большое количество элементов в модели позволяет точно описать экспериментальные данные, но существенно усложняет расчеты.

В наследственной теории ползучести (Больцман, 1874) учитывается влияние истории нагружения материала на его деформации в рассматриваемый момент времени, а форма связи между напряжениями и деформациями интегральная.

, (5.19)

где 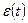- деформация в рассматриваемый момент времени t; и 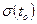- напряжения, развивающиеся соответственно к моментам времени t и t_o; t – текущая координата времени; и t_o; t_о – момент времени, соответствующий приложению нагрузки, вызывающей напряжение 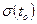, которое действует в течение отрезка времени dt_o; E_el - модуль мгновенной деформации скелета грунта; k(t-t_o) - функция влияния (ядро ползучести), характеризующее скорость деформации ползучести при постоянном напряжении, отнесённую к единице.

. (5.20)

За нижний предел интегрирования 0 часто принимается момент начала загружения. Ядро ползучести с точностью до постоянной представляет из себя скорость деформации ползучести при единичном напряжении. Первый член формулы (5.19) дает мгновенную деформацию, второй - деформацию ползучести.

Решением уравнения (5.19) служит выражение

. (5.21)

Функция R(t – t_o) называется резольвентой ядра ползучести k(t - t_o). Она представляет из себя с точностью до постоянной скорость релаксации напряжения при постоянной единичной деформации.

К наиболее часто употребляемым ядрам ползучести относятся экспоненциальное ядро, степенное ядро и ядро Больцмана, имеющие соответственно вид

, (5.22)

где δ, δ₁, и δ₂ - постоянные коэффициенты, определяемые по экспериментальным данным.

Наследственные теории ползучести являются наиболее общими. Простейшие теории ползучести и метод реологических моделей могут рассматриваться их частными случаями. В случае действия переменных нагрузок, необходимости нелинейности связи между напряжениями и деформациями в грунте предпочтительно применение наследственной теории ползучести.

Теория ползучести является наиболее сложным, но и наиболее общим разделом механики твердого тела. Ее следует использовать в случае необходимости прогноза на длительный период деформаций грунтов и устойчивости оснований ответственных сооружений.

Общие положения применения механики жидкости и газа к грунтам

Увеличение влажности грунта приближает его свойства к вязкой текучей жидкости, которые описываются уравнениями гидродинамики. Повышение содержания пузырьков газа в порах грунта или поровой воде вызывает нелинейное увеличение его упругих деформаций. Сжатие газообразной фазы определяется уравнениями теории газа. Для многофазных грунтов важными являются вопросы о границах применимости к ним разделов механики твердого тела, жидкости и газа.

Для идеальной жидкости постулируется, что она изотропна, несжимаема и не обладает внутренним трением. По закону Паскаля по всем направлениям в рассматриваемой точке жидкости давления одинаковы. Давление от собственного веса в жидкости вычисляют по формуле

, (5.23)

где γ_w, - удельный вес жидкости; h - высота столба жидкости над рассматриваемой точкой.

Свойства идеальной жидкости использовались Н.М. Герсевановым (1933) и В.А. Флориным (1938) для описания уплотнения грунтовой массы, то есть глинистого грунта, поры которого полностью заполнены несжимаемой жидкостью.

В реальных условиях газ в порах грунта содержится в свободном виде или растворенным в воде в виде пузырьков. От действия на основание нагрузок от сооружений промышленного и гражданского строительства сопротивлением сжатию свободного газа часто можно пренебречь. При устройстве глубоких подземных сооружений ниже уровня подземных вод, в связи с высокими давлениями в воде пор грунта необходим учет растворимости газа в воде и ее сжимаемости. Приближенно учет сжимаемости газа, содержащегося в воде, может быть осуществлен с помощью коэффициента объемной сжимаемости газа

, (5.24)

где. s_о - начальное содержание газа в пузырьках воды; μ - коэффициент растворимости газа в воде (коэффициент Генри): п пористость грунта; - начальное давление в газообразной фазе; р_а - атмосферное давление; u_w - избыточное, или поровое давление воды. Значения коэффициента μ при атмосферном давлении - 0.0292.

При течении вязких жидкостей следует учитывать в ней внутреннее трение согласно закону Ньютона

, (5.25)

где V - скорость течения жидкости; η - коэффициент внутреннего трения или вязкости.

Н.Н. Маслов (1968) рассматривал грунт как вязкую жидкость (однофазную систему), свойства которой (в том числе коэффициент вязкости) зависят от “плотности - влажности”.

⇐ Предыдущая12345

Поделиться:

Воспользуйтесь поиском по сайту: